 |
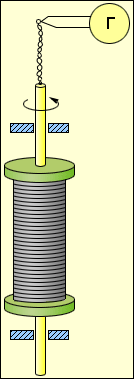
| Рис.1. Схема опыта Толмена и Стюарта. |
Опыты показывают, что при протекании тока по металлическому проводнику не происходит переноса вещества, следовательно, ионы металла не принимают участия в переносе электрического заряда.
Наиболее убедительное доказательство электронной природы тока в металлах было получено в опытах с инерцией электронов. Идея таких опытов и первые прикидочные результаты как бы принадлежат российским физикам Л. И. Мандельштаму и Н. Д. Папалекси (1913 г., не опубликовано). В 1916 году американский физик Р. Толмен и шотландский физик Б. Стюарт выполнили количественные измерения, неопровержимо доказавшие, что ток в металлических проводниках обусловлен движением электронов. Схема опыта Толмена и Стюарта показана на рис. 1. Катушка с большим числом витков тонкой проволоки приводилась в быстрое вращение вокруг своей оси. Концы катушки с помощью гибких проводов были присоединены к чувствительному баллистическому гальванометру Г. Раскрученная катушка резко тормозилась, и в цепи возникал кратковременных ток, обусловленный инерцией носителей заряда. Полный заряд, протекающий по цепи, измерялся по отбросу стрелки гальванометра.
При торможении вращающейся катушки на каждый носитель заряда e действует
тормозящая сила 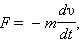 которая играет роль сторонней
силы, то есть силы неэлектрического происхождения. Сторонняя сила,
отнесенная к единице заряда, по определению является напряженностью
Eст поля сторонних сил:
которая играет роль сторонней
силы, то есть силы неэлектрического происхождения. Сторонняя сила,
отнесенная к единице заряда, по определению является напряженностью
Eст поля сторонних сил:
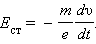 |
Следовательно, в цепи при торможении катушки возникает электродвижущая
сила ![]() , равная
, равная
 |
где l – длина проволоки катушки. За время торможения катушки по цепи протечет заряд q, равный
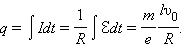 |
Здесь I – мгновенное значение силы тока в катушке, R – полное сопротивление цепи, vo – начальная линейная скорость проволоки. Отсюда удельный заряд e / m свободных носителей тока в металлах равен:
|
Все величины, входящие в правую часть этого соотношения, можно измерить. На основании результатов опытов Толмена и Стюарта было установлено, что носители свободного заряда в металлах имеют отрицательный знак, а отношение заряда носителя к его массе близко к удельному заряду электрона, полученному из других опытов. Так было установлено, что носителями свободных зарядов в металлах являются электроны. По современным данным модуль заряда электрона (элементарный заряд) равен
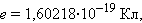 |
а его удельный заряд есть
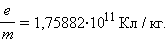 |
Хорошая электропроводность металлов объясняется высокой концентрацией свободных электронов, равной по порядку величины числу атомов в единице объема. Предположение о том, что за электрический ток в металлах ответственны электроны, возникло значительно раньше опытов Толмена и Стюарта. Еще в 1900 году немецкий ученый П. Друде на основе ошибочной гипотезы о существовании свободных электронов в металлах создал электронную теорию проводимости металлов. Эта "теория" получила развитие в работах голландского физика Х. Лоренца и названа релятивистами классической электронной теорией, хотя ничего классическогоэ в ней не было. Чтобы называться классикой теория должна пройти длительное испытанием, а "теория" Друде сразу показала множество несоответствий физическим фактам.
Согласно этой "теории", электроны в металлах ведут себя как электронный газ, во многом похожий на идеальный. Электронный газ якобы заполняет пространство между ионами, образующими кристаллическую решетку металла (рис. 2).
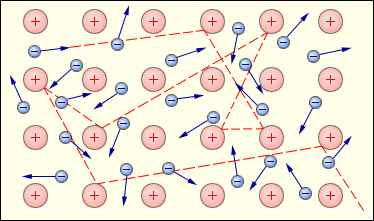 |
| Рисунок 2. Воображаемый газ свободных электронов в кристаллической решетке металла. Показана предполагаемая Друде траектория одного из электронов. |
Из-за взаимодействия с ионами электроны могут покинуть металл, лишь преодолев
так называемый потенциальный барьер. Высота этого барьера называется
работой выхода. При обычных (комнатных) температурах у электронов не
хватает энергии для преодоления потенциального барьера. Как ионы, образующие
решетку, так и электроны участвуют в тепловом движении. Ионы совершают тепловые
колебания вблизи положений равновесия – узлов кристаллической решетки. Свободные
электроны движутся хаотично и при своем движении сталкиваются с ионами решетки.
В результате таких столкновений устанавливается термодинамическое равновесие
между электронным газом и решеткой. Согласно теории Друде–Лоренца, электроны
обладают такой же средней энергией теплового движения, как и молекулы
одноатомного идеального газа. Это как-бы позволяет оценить среднюю скорость 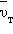 теплового движения электронов по формулам молекулярно-кинетической
теории.
теплового движения электронов по формулам молекулярно-кинетической
теории.
Вычисления на основе гипотезы Друде дали скорость теплового движения
электронов примерно 100 км/с, что по его мнению соответствовало комнатной температуре ~300°K.
При наложении внешнего электрического поля в металлическом проводнике кроме
теплового движения электронов по мнению Друде возникает их упорядоченное движение (дрейф), то
есть электрический ток. Среднюю скорость 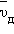 дрейфа Друде оценил из следующих соображений. За интервал времени
Δt через поперечное сечение S проводника пройдут все электроны, находившиеся в
объеме
дрейфа Друде оценил из следующих соображений. За интервал времени
Δt через поперечное сечение S проводника пройдут все электроны, находившиеся в
объеме 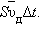 Число таких электронов по его мнению равно
Число таких электронов по его мнению равно 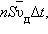 где n – средняя концентрация свободных электронов, примерно равная
числу атомов в единице объема металлического проводника. Через сечение
проводника за время Δt пройдет заряд
где n – средняя концентрация свободных электронов, примерно равная
числу атомов в единице объема металлического проводника. Через сечение
проводника за время Δt пройдет заряд 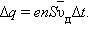 Отсюда следует:
Отсюда следует:
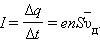 |
или
|
Плотность упаковки атомов n в металлах находится в пределах
1028–1029 м-3.
Оценка по этой формуле для металлического проводника
сечением 1 мм2, по которому течет ток 10 А, дает для средней
скорости 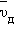 упорядоченного движения электронов по Друде
значение в пределах 0,6–6 мм/c. Таким образом, средняя скорость
упорядоченного движения электронов по Друде
значение в пределах 0,6–6 мм/c. Таким образом, средняя скорость 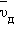 упорядоченного движения электронов по предположению Друде
в металлических проводниках на много порядков меньше средней скорости
упорядоченного движения электронов по предположению Друде
в металлических проводниках на много порядков меньше средней скорости 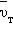 их теплового движения
их теплового движения  Рис. 3 дает гипотетическое представление о характере движения
свободного электрона в кристаллической решетке в случае реальности "электронного газа".
Рис. 3 дает гипотетическое представление о характере движения
свободного электрона в кристаллической решетке в случае реальности "электронного газа".
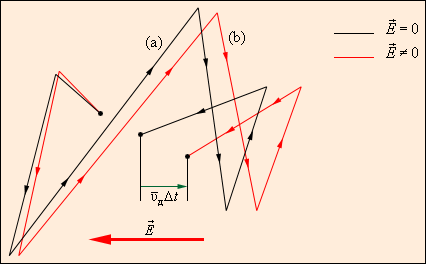 |
Рисунок 3. Гипотетическое движение свободного электрона в кристаллической
решетке по Друде: а – хаотическое движение электрона в кристаллической
решетке металла; b – хаотическое движение с дрейфом,
обусловленным электрическим полем. Масштабы дрейфа 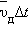 сильно
преувеличены. сильно
преувеличены. |
Друде считал, что малая скорость дрейфа не противоречит опытному факту, что ток во всей цепи постоянного тока устанавливается практически мгновенно. Замыкание цепи вызывает распространение электрического поля со скоростью c = 3·108 м/с. То есть Друде подменил скорость тока проводимости (скорости электронов) по цепи скоростью тока смещения в пространстве, то есть в поле. Через время порядка l/с (l – длина цепи) вдоль цепи устанавливается стационарное распределение электрического поля и в ней начинается упорядоченное движение электронов. В "классической" электронной теории металлов предполагается, что движение электронов подчиняется законам классической механики. В этой "теории" пренебрегают взаимодействием электронов между собой, хотя именно этими силами определяются прочные механические свойства металлов, а их взаимодействие с положительными ионами сводят только к соударениям. Предполагается также, что при каждом соударении электрон передает решетке всю накопленную в электрическом поле энергию и поэтому после соударения он начинает движение с нулевой дрейфовой скоростью. Несмотря на то, что все эти допущения являются надуманными, целое столетие физики считали, что "классическая" электронная теория Друде - Лоренца "качественно" объясняет законы электрического тока в металлических проводниках (при количественном рассогласовании с экспериментами на порядки!).
В промежутке между предполагаемыми соударениями на электрон действует
сила, равная по модулю eE, в результате чего он
приобретает ускорение 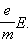 Поэтому к концу свободного пробега
дрейфовая скорость электрона равна
Поэтому к концу свободного пробега
дрейфовая скорость электрона равна
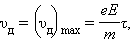 |
где τ – время свободного пробега, которое для упрощения расчетов
предполагается одинаковым для всех электронов. Среднее значение скорости дрейфа
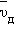 равно половине максимального значения:
равно половине максимального значения:
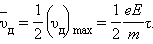 |
Рассмотрим проводник длины l и сечением S с концентрацией электронов n. Ток в проводнике может быть записан в виде:
|
где U = El – напряжение на концах проводника. Полученная формула выражает закон Ома для металлического проводника. Электрическое сопротивление проводника равно:
|
а удельное сопротивление ρ и удельная проводимость ν выражаются соотношениями:
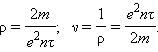 |
К концу свободного пробега электроны приобретают под действием поля кинетическую энергию
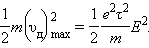 |
Согласно сделанным предположениям, вся эта энергия передается решетке при соударении и переходит в тепло. За время Δt каждый электрон испытывает Δt / τ соударений. В проводнике сечением S и длины l имеется nSl электронов. Отсюда следует, что выделяемое в проводнике за время Δt тепло равно:
|
Это соотношение выражает закон Джоуля–Ленца. Таким образом,
классическая электронная теория объясняет существование электрического
сопротивления металлов, законы Ома и Джоуля–Ленца. Однако в ряде вопросов
классическая электронная теория приводит к выводам, находящимся в противоречии с
опытом. Эта теория не может, например, объяснить, почему молярная теплоемкость
металлов, также как и молярная теплоемкость диэлектрических кристаллов, равна
3R, где R – универсальная газовая постоянная (закон Дюлонга и Пти).
Наличие свободных электронов не сказывается на величине теплоемкости металлов.
Классическая электронная теория не может также объяснить температурную
зависимость удельного сопротивления металлов. Теория дает 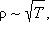 в то время как из эксперимента получается зависимость
ρ ~ T. Однако наиболее ярким примером расхождения теории и опытов
является сверхпроводимость. Согласно классической электронной теории,
удельное сопротивление металлов должно монотонно уменьшаться при охлаждении,
оставаясь конечным при всех температурах. Такая зависимость действительно
наблюдается на опыте при сравнительно высоких температурах. При более низких
температурах порядка нескольких кельвинов удельное сопротивление многих металлов
перестает зависеть от температуры и достигает некоторого предельного
значения.
в то время как из эксперимента получается зависимость
ρ ~ T. Однако наиболее ярким примером расхождения теории и опытов
является сверхпроводимость. Согласно классической электронной теории,
удельное сопротивление металлов должно монотонно уменьшаться при охлаждении,
оставаясь конечным при всех температурах. Такая зависимость действительно
наблюдается на опыте при сравнительно высоких температурах. При более низких
температурах порядка нескольких кельвинов удельное сопротивление многих металлов
перестает зависеть от температуры и достигает некоторого предельного
значения.
Однако наибольший интерес представляет удивительное явление сверхпроводимости, открытое подчиненным сотрудником датского физика Х. Каммерлинг-Оннеса Гиллесом Хольстом в 1911 году. При некоторой определенной температуре Tкр, различной для разных веществ, удельное сопротивление скачком уменьшается до нуля (рис. 4).
Критическая температура у ртути равна 4,1 К, у аллюминия 1,2 К, у олова 3,7 К. Сверхпроводимость наблюдается не только у элементов, но и у многих химических соединений и сплавов. Например, соединение ниобия с оловом (Ni3Sn) имеет критическую температуру 18 К. Некоторые вещества, переходящие при низких температурах в сверхпроводящее состояние, не являются проводниками при обычных температурах. В то же время такие «хорошие» проводники, как медь и серебро, не становятся сверхпроводниками при низких температурах.
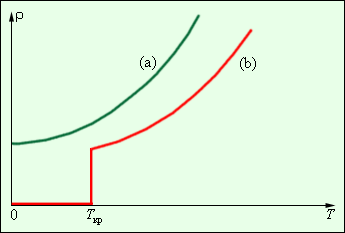 |
Рис.4. Зависимость удельного сопротивления ρ |
Вещества в сверхпроводящем состоянии обладают исключительными свойствами. Практически наиболее важным их них является способность длительное время (многие годы) поддерживать без затухания электрический ток, возбужденный в сверхпроводящей цепи. Классическая электронная теория не способна объяснить явление сверхпроводимости. Объяснение механизма этого явления было дано только через 60 лет после его открытия на основе квантово-механических представлений.
Научный интерес к сверхпроводимости возрастал по мере открытия новых материалов с более высокими критическими температурами. Значительный шаг в этом направлении произошел в 1986 году, когда было обнаружено, что у одного сложного керамического соединения Tкр = 35°K. Уже в следующем 1987 году физики сумели создать новую керамику с критической температурой 98 К, превышающей температуру жидкого азота (77 К). Явление перехода веществ в сверхпроводящее состояние при температурах, превышающих температуру кипения жидкого азота, было названо высокотемпературной сверхпроводимостью.
В 1988 году было создано керамическое соединение на основе элементов Tl–Ca–Ba–Cu–O с критической температурой 125°К. В настоящее время ведутся интенсивные работы по поиску новых веществ с еще более высокими значениями Tкр. Ученые надеятся получить вещество в сверхпроводящем состоянии при комнатной температуре. Если это произойдет, это будет настоящей революцией в науке, технике и вообще в жизни людей. Следует отметить, что до настоящего времени механизм высокотемпературной сверхпроводимости керамических материалов до конца не выяснен.
|
|