Плотность состояний - число возможных физически неэквивалентных энергетич. состояний в малом
интервале энергии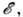 отнесённое к ширине интервала
отнесённое к ширине интервала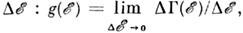 где
где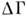 - число состояний
с энергиями между
- число состояний
с энергиями между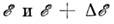 (с учётом возможного вырождения энергетич. состояний). Для колебат. степеней
свободы системы часто имеют в виду спектральную П. с.
(с учётом возможного вырождения энергетич. состояний). Для колебат. степеней
свободы системы часто имеют в виду спектральную П. с.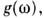 определяемую по числу состояний на интервал частот
определяемую по числу состояний на интервал частот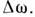 В этом случае
В этом случае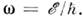
П. с. имеет смысл вводить, либо если система
обладает непрерывным энергетич. спектром, либо если спектр дискретен, когда
расстояние между соседними энергетич. уровнями мало по сравнению с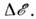 Если состояния системы определяются широко разнесёнными по
Если состояния системы определяются широко разнесёнными по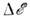 дискретными уровнями, каждый из к-рых расщепляется в области, узкие по
сравнению с расстоянием между уровнями, то вводят П. с. вблизи каждого
дискретного уровня. Это имеет место, напр., при движении электронов в сильном
квантующем магн. поле (см. квантовые уровни - Онсагера
квантование). Для свободных нерелятивистских частиц со спином s состояния характеризуются импульсом р и проекцией спина, а энергия
дискретными уровнями, каждый из к-рых расщепляется в области, узкие по
сравнению с расстоянием между уровнями, то вводят П. с. вблизи каждого
дискретного уровня. Это имеет место, напр., при движении электронов в сильном
квантующем магн. поле (см. квантовые уровни - Онсагера
квантование). Для свободных нерелятивистских частиц со спином s состояния характеризуются импульсом р и проекцией спина, а энергия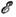 = р2/2т (т - масса) П. с. зависит только от р:
= р2/2т (т - масса) П. с. зависит только от р: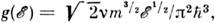 где
множитель v = 2s + 1 учитывает вырождение по спину
s. Для квазичастиц твёрдого тела эта зависимость является более сложной,
напрю для электронов проводимости с энергетич. спектром
где
множитель v = 2s + 1 учитывает вырождение по спину
s. Для квазичастиц твёрдого тела эта зависимость является более сложной,
напрю для электронов проводимости с энергетич. спектром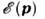
Знаете ли Вы, что такое "Большой Взрыв"?
Согласно рупору релятивистской идеологии Википедии "Большой взрыв (англ. Big Bang) - это космологическая модель, описывающая раннее развитие Вселенной, а именно - начало расширения Вселенной, перед которым Вселенная находилась в сингулярном состоянии. Обычно сейчас автоматически сочетают теорию Большого взрыва и модель горячей Вселенной, но эти концепции независимы и исторически существовало также представление о холодной начальной Вселенной вблизи Большого взрыва. Именно сочетание теории Большого взрыва с теорией горячей Вселенной, подкрепляемое существованием реликтового излучения..."
В этой тираде количество нонсенсов (бессмыслиц) больше, чем количество предложений, иначе просто трудно запутать сознание обывателя до такой степени, чтобы он поверил в эту ахинею.
На самом деле взорваться что-либо может только в уже имеющемся пространстве.
Без этого никакого взрыва в принципе быть не может, так как "взрыв" - понятие, применимое только внутри уже имеющегося пространства. А раз так, то есть, если пространство вселенной уже было до БВ, то БВ не может быть началом Вселенной в принципе. Это во-первых.
Во-вторых, Вселенная - это не обычный конечный объект с границами, это сама бесконечность во времени и пространстве. У нее нет начала и конца, а также пространственных границ уже по ее определению: она есть всё (потому и называется Вселенной).
В третьих, фраза "представление о холодной начальной Вселенной вблизи Большого взрыва" тоже есть сплошной нонсенс.
Что могло быть "вблизи Большого взрыва", если самой Вселенной там еще не было? Подробнее читайте в
FAQ по эфирной физике.
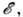 отнесённое к ширине интервала
отнесённое к ширине интервала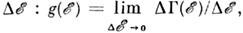 где
где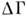 - число состояний
с энергиями между
- число состояний
с энергиями между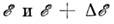 (с учётом возможного вырождения энергетич. состояний). Для колебат. степеней
свободы системы часто имеют в виду спектральную П. с.
(с учётом возможного вырождения энергетич. состояний). Для колебат. степеней
свободы системы часто имеют в виду спектральную П. с.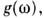 определяемую по числу состояний на интервал частот
определяемую по числу состояний на интервал частот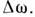 В этом случае
В этом случае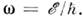
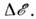 Если состояния системы определяются широко разнесёнными по
Если состояния системы определяются широко разнесёнными по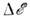 дискретными уровнями, каждый из к-рых расщепляется в области, узкие по
сравнению с расстоянием между уровнями, то вводят П. с. вблизи каждого
дискретного уровня. Это имеет место, напр., при движении электронов в сильном
квантующем магн. поле (см. квантовые уровни - Онсагера
квантование). Для свободных нерелятивистских частиц со спином s состояния характеризуются импульсом р и проекцией спина, а энергия
дискретными уровнями, каждый из к-рых расщепляется в области, узкие по
сравнению с расстоянием между уровнями, то вводят П. с. вблизи каждого
дискретного уровня. Это имеет место, напр., при движении электронов в сильном
квантующем магн. поле (см. квантовые уровни - Онсагера
квантование). Для свободных нерелятивистских частиц со спином s состояния характеризуются импульсом р и проекцией спина, а энергия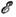 = р2/2т (т - масса) П. с. зависит только от р:
= р2/2т (т - масса) П. с. зависит только от р: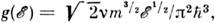 где
множитель v = 2s + 1 учитывает вырождение по спину
s. Для квазичастиц твёрдого тела эта зависимость является более сложной,
напрю для электронов проводимости с энергетич. спектром
где
множитель v = 2s + 1 учитывает вырождение по спину
s. Для квазичастиц твёрдого тела эта зависимость является более сложной,
напрю для электронов проводимости с энергетич. спектром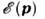
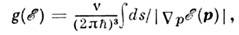
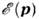 = const в пространстве квазиимпульсов, ds - элемент площади на этой
поверхности;
= const в пространстве квазиимпульсов, ds - элемент площади на этой
поверхности;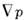 - градиент в пространстве квазиимпульсов. Для спектральной П. с.
- градиент в пространстве квазиимпульсов. Для спектральной П. с.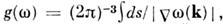 где k -
где k - 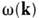 = const. Подынтегральные выражения для П. с. имеют особенности в точках,
в к-рых
= const. Подынтегральные выражения для П. с. имеют особенности в точках,
в к-рых 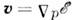 обращаются в 0. Эти точки наз. критическими, а соответствующие особенности
в
обращаются в 0. Эти точки наз. критическими, а соответствующие особенности
в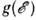 -
Ван
Хова особенностями.
-
Ван
Хова особенностями.
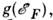 входящая непосредственно в виде множителя в большинство макроскопич. характеристик
системы. Для
входящая непосредственно в виде множителя в большинство макроскопич. характеристик
системы. Для 
