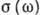 проводников (металлов, полупроводников и др.), посредством к-рой задается линейная
связь между плотностью тока j и напряженностью приложенного перем. электрич.
поля частоты
проводников (металлов, полупроводников и др.), посредством к-рой задается линейная
связь между плотностью тока j и напряженностью приложенного перем. электрич.
поля частоты 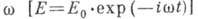
Высокочастотная проводимость - характеристика 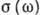 проводников (металлов, полупроводников и др.), посредством к-рой задается линейная
связь между плотностью тока j и напряженностью приложенного перем. электрич.
поля частоты
проводников (металлов, полупроводников и др.), посредством к-рой задается линейная
связь между плотностью тока j и напряженностью приложенного перем. электрич.
поля частоты 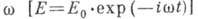
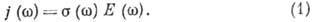
Выражение (1) естественным образом обобщает Ома закон .Оно справедливо в локальном пределе, когда
т. н. эффективная длина iэф свободного пробега носителей заряда
(для определенности электронов) ограничена:
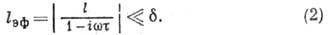
Здесь  -
характерный размер, на к-ром изменяется поле
-
характерный размер, на к-ром изменяется поле 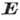 ,
,
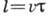 - длина свободного
пробега электрона,
- длина свободного
пробега электрона, 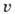 - ср. скорость электронов (в металлах и вырожденных полупроводниках
- ср. скорость электронов (в металлах и вырожденных полупроводниках 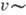 107-108
см/с, в обычных полупроводниках
107-108
см/с, в обычных полупроводниках 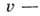 скорость теплового движения),
скорость теплового движения), 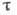 -
время между столкновениями (время релаксации) электронов.
Обычно
-
время между столкновениями (время релаксации) электронов.
Обычно 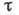 лежит
в пределах 10-9- 10-13 с и зависит от температуры и чистоты
проводника и, кроме того, может изменяться с частотой.
лежит
в пределах 10-9- 10-13 с и зависит от температуры и чистоты
проводника и, кроме того, может изменяться с частотой.
В изотропных средах высокочастотная проводимость определяется (по порядку величины) соотношением:
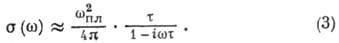
Здесь 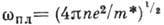 - плазменная частота электронов, п - их концентрация, m*-
эффективная масса электрона, е - его заряд. В анизотропных средах
- плазменная частота электронов, п - их концентрация, m*-
эффективная масса электрона, е - его заряд. В анизотропных средах 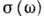 - тензор. При выполнении условия (2) описание высокочастотной проводимости возможно путём введения
т. н. эффективной диэлектрич. проницаемости, учитывающей вклад электронов:
- тензор. При выполнении условия (2) описание высокочастотной проводимости возможно путём введения
т. н. эффективной диэлектрич. проницаемости, учитывающей вклад электронов:
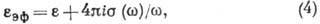
где 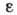 - диэлектрич. проницаемость ионной решётки. Зависимость
- диэлектрич. проницаемость ионной решётки. Зависимость 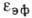 от частоты (временная дисперсия
от частоты (временная дисперсия 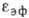 )
в электронных проводниках, в отличие от диэлектриков, проявляется, начиная с
низких частот. Это - следствие наличия свободных носителей заряда, способных
изменять свою энергию на сколь угодно малую величину.
Роль характерной частоты, определяющей временную дисперсию, при низких частотах
играет частота столкновений электронов
)
в электронных проводниках, в отличие от диэлектриков, проявляется, начиная с
низких частот. Это - следствие наличия свободных носителей заряда, способных
изменять свою энергию на сколь угодно малую величину.
Роль характерной частоты, определяющей временную дисперсию, при низких частотах
играет частота столкновений электронов 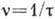 , при высоких - плазменная частота. При
, при высоких - плазменная частота. При  вклад электронов проводимости в
вклад электронов проводимости в  мал и различие между проводником и диэлектриком исчезает.
мал и различие между проводником и диэлектриком исчезает.
При 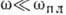 ток проводимости обусловливает быстрое затухание эл.- магн. волны в тонком слое
толщиной
ток проводимости обусловливает быстрое затухание эл.- магн. волны в тонком слое
толщиной 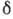 вблизи
поверхности проводника (см. Скин-эффект ).Если при этом оказывается,
что
вблизи
поверхности проводника (см. Скин-эффект ).Если при этом оказывается,
что 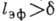 , то
проводимость становится нелокальной: ток определяется значениями поля в области
с размерами порядка
, то
проводимость становится нелокальной: ток определяется значениями поля в области
с размерами порядка 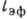 .
В этом случае необходим учет дисперсии пространственной,
вследствие которой высокочастотная проводимость зависит от квазиимпульса, определяя связь между пространственными Фурье-компонентами
плотности тока j и электрич. поля E. Учёт пространств. дисперсии необходим при низких темп-pax, когда длина свободного пробега становится достаточно
большой.
.
В этом случае необходим учет дисперсии пространственной,
вследствие которой высокочастотная проводимость зависит от квазиимпульса, определяя связь между пространственными Фурье-компонентами
плотности тока j и электрич. поля E. Учёт пространств. дисперсии необходим при низких темп-pax, когда длина свободного пробега становится достаточно
большой.
При наложении постоянного магнитного поля H
высокочастотная проводимость претерпевает существенные изменения: в 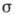 даже
в случае изотропного проводника появляются недиагональные холловские компоненты
(см. Холла эффект; )кроме того, временная дисперсия определяется также
и значением циклотронной частоты
даже
в случае изотропного проводника появляются недиагональные холловские компоненты
(см. Холла эффект; )кроме того, временная дисперсия определяется также
и значением циклотронной частоты 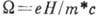 . Последнее играет особенно важную роль при
. Последнее играет особенно важную роль при  ,
приводя к появлению циклотронного резонанса слабозатухающих волн - геликонов, магнитоплазменных (магнитогидродинамических), циклотронных и доплеронов, а также размерных эффектов в магн. поле.
,
приводя к появлению циклотронного резонанса слабозатухающих волн - геликонов, магнитоплазменных (магнитогидродинамических), циклотронных и доплеронов, а также размерных эффектов в магн. поле.
T. к. поле и ток в проводниках
сосредоточены вблизи поверхности, то существующие в магн. поле магнитные
поверхностные уровни приводят к резонансным особенностям в относительно
слабых полях, когда 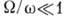 .
В сильных магн. полях, удовлетворяющих условию
.
В сильных магн. полях, удовлетворяющих условию  ,
в высокочастотной проводимости металлов и вырожденных полупроводниках проявляются квантовые осцилляции. Наличие у проводника магн. свойств (парамагнетизма, ферромагнетизма, антиферромагнетизма)
отражается на высокочастотной проводимости благодаря зависимости его магн. восприимчивости от
,
в высокочастотной проводимости металлов и вырожденных полупроводниках проявляются квантовые осцилляции. Наличие у проводника магн. свойств (парамагнетизма, ферромагнетизма, антиферромагнетизма)
отражается на высокочастотной проводимости благодаря зависимости его магн. восприимчивости от 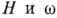 .
.
Знание высокочастотной проводимости позволяет
вычислить распределение электрич. поля в проводнике, поверхностный импеданс,
характеризующий амплитуду и фазу отражаемой проводником волны, и коэф. прохождения
волны через образцы ограниченных размеров (см. Импеданс).

В. С. Эдельман
Вещество и поле не есть что-то отдельное от эфира, также как и человеческое тело не есть что-то отдельное от атомов и молекул его составляющих. Оно и есть эти атомы и молекулы, собранные в определенном порядке. Также и вещество не есть что-то отдельное от элементарных частиц, а оно состоит из них как базовой материи. Также и элементарные частицы состоят из частиц эфира как базовой материи нижнего уровня. Таким образом, всё, что есть во вселенной - это есть эфир. Эфира 100%. Из него состоят элементарные частицы, а из них всё остальное. Подробнее читайте в FAQ по эфирной физике.
|
|