
Циклотронный резонанс - резонансное поглощение
эл--магн. энергии электронными проводниками (полупроводниками, металлами), помещёнными
в пост. магн. поле, на частотах, равных или кратных циклотронной частоте носителей
заряда (электронов и дырок). Ц. р. (по старой терминологии-диамагнитный резонанс)
предсказан Я. Г. Дорфманом в 1951 и P. Б. Динглем в 1952, экспериментально обнаружен
Ч. Киттелем (Ch. Kittel) с сотрудниками в 1953.
Явление Ц. р. может быть объяснено на основе
законов классич. физики. Носители заряда в пост. магн. поле H
движутся по спирали с осью вдоль H. В плоскости, перпендикулярной
H, движение является периодическим с циклотронной частотой:

где е-заряд, тс - эфф.
величина, наз. циклотронной массой носителей заряда. Очевидно, с той
же частотой wc, поворачивается вектор скорости частицы
u. Если при этом частица находится в периодич. электрич. поле E(t)с частотой w. то энергия, поглощаемая ею в единицу времени, равная
eEu, также оказывается периодич. функцией времени с разностной угл. частотой (wc
- w). С той же частотой (wс
- w) меняются радиус спирали и кинетич. энергия носителя. При w
= wс.
носитель движется по раскручивающейся спирали и поглощаемая мощность возрастает.
Рассеяние носителей заряда в твёрдом теле ограничивает это возрастание:
при w = wс
поглощаемая мощность имеет максимум, если рассеяние является достаточно слабым.
Последнее условие сводится к требованию, чтобы носитель успевал сделать много
оборотов по спирали за время т релаксации импульса носителя (время между
двумя актами рассеяния). Это приводит к условию наблюдения Ц. р.:
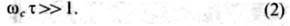
Описанная картина Ц. р. пригодна для достаточно
слабого магн. поля H, в к-ром можно пренебречь квантованием
кинетич. энергии поперечного (относительно H)движения
носителей.Квантование отсутствует, если
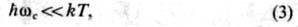
где T-абс. темп-pa. Ц. р. в таких полях
наз. классическим.
В противоположном случае (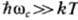 ),
в т. н. квантующем магн. поле (см. Гальваномагнитные явления), адекватным
является описание Ц. р. на квантовом языке. В полях H, для
к-рых
),
в т. н. квантующем магн. поле (см. Гальваномагнитные явления), адекватным
является описание Ц. р. на квантовом языке. В полях H, для
к-рых 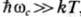 , носители
заряда находятся на нулевом уровне (в случае невырожденных носителей).
Под действием электрич. поля эл--магн. волны E(t)носители
переходят с нулевого уровня на первый,
, носители
заряда находятся на нулевом уровне (в случае невырожденных носителей).
Под действием электрич. поля эл--магн. волны E(t)носители
переходят с нулевого уровня на первый,
что приводит к поглощению эл--магн. энергии,
к-рое имеет максимум на частоте, при к-рой энергия кванта излучения 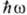 равна расстоянию между соседними уровнями:
равна расстоянию между соседними уровнями: 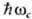 . Максимум отчётливо выражен, если уширение уровней, обусловленное временем
релаксации т, мало по сравнению с расстоянием между ними:
. Максимум отчётливо выражен, если уширение уровней, обусловленное временем
релаксации т, мало по сравнению с расстоянием между ними: 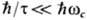 (см. ниже).
(см. ниже).
Циклотронный резонанс в полупроводниках
Ц. р.- важный метод исследования полупроводников. Он даёт возможность определить закон дисперсии (энергетич. спектр) носителей
заряда  (р)
(р - квазиимпульс носителей), знак заряда носителей, эфф. массу,
концентрацию, времена жизни; позволяет изучить механизм рассеяния носителей
заряда, разогрев носителей переменным полем и др. (см. ниже). Преимуществом
Ц. р. по сравнению с др. методами является его избирательность - возможность
подбором частоты выделить определ. группу носителей в полупроводнике.
(р)
(р - квазиимпульс носителей), знак заряда носителей, эфф. массу,
концентрацию, времена жизни; позволяет изучить механизм рассеяния носителей
заряда, разогрев носителей переменным полем и др. (см. ниже). Преимуществом
Ц. р. по сравнению с др. методами является его избирательность - возможность
подбором частоты выделить определ. группу носителей в полупроводнике.
Ц. р. в полупроводниках наблюдается на частотах
1010-1012 Гц в полях 1 -100 кЭ. T. к. концентрация носителей
заряда мала (обычно не превосходит 1014- 1015 см-3
), то эл--магн. волны проникают в образец на большую глубину, значительно превосходящую
диаметры орбит электронов (порядка мкм). T. о., носители движутся в однородном
электрич. поле, и Ц. р., как правило, наблюдается только при w
= wс
Определение эффективной массы носителей. В
простейшем случае изотропного квадратичного закона дисперсии носителей изоэнергетич.
поверхность 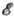 (p)
=
(p)
=  -сфера (см.
Зонная теория ).Определение частоты wс
позволяет найти скалярную эффективную массу носителей т, к-рая
совпадает с циклотронной массой тс. В случае более сложных
законов дисперсии эфф. масса отличается от циклотронной массы. Для эллипсоидальных
изоэнергетич. поверхностей тс зависит только от направления
H, что позволяет определить гл. значения тензора эфф. масс.
Напр., для электронов в Ge (кубич. симметрия) изоэнергетич. поверхность - совокупность
4 сфероидов (двухосных эллипсоидов), оси вращения к-рых направлены вдоль диагоналей
куба. т. е. кристаллографич. осей [111]. В этом случае циклотронная частота
-сфера (см.
Зонная теория ).Определение частоты wс
позволяет найти скалярную эффективную массу носителей т, к-рая
совпадает с циклотронной массой тс. В случае более сложных
законов дисперсии эфф. масса отличается от циклотронной массы. Для эллипсоидальных
изоэнергетич. поверхностей тс зависит только от направления
H, что позволяет определить гл. значения тензора эфф. масс.
Напр., для электронов в Ge (кубич. симметрия) изоэнергетич. поверхность - совокупность
4 сфероидов (двухосных эллипсоидов), оси вращения к-рых направлены вдоль диагоналей
куба. т. е. кристаллографич. осей [111]. В этом случае циклотронная частота
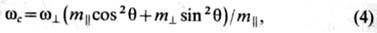
где w |
= |е|Н/т | с; q - угол между полем H
и осью [111]; m||, m | -продольная
и поперечная эфф. массы. Если H лежит в плоскости (110), то 2
из 4 сфероидов имеют одинаковый угол q,
т. е. одинаковые wc,
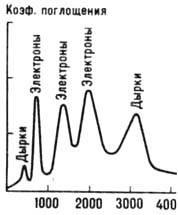
и при произвольном q для электронов наблюдается 3 пика Ц. р. (рис. 1).
Рис. 1. Циклотронный резонанс в Ge при wc/2p = 24 ГГц, T= 4,2 К; H направлено в плоскости (110) под углом 600 к кри сталлографической оси [110].
Поворачивая кристалл в поле H, можно определить зависимость mс(q)
(рис. 2). Выбрав 2 значения для двух q,
можно определить m|| и m | .
Для изоэнергетич. поверхностей более сложной
формы, чем эллипсоидальная, wс
оказывается зависящей не только от ориентации поля H. но
и от проекции рH квазиимпульса носителей на направление
H. В этом случае возникает разброс wc,
и максимум поглощения наблюдается при нек-ром ср. значении -wc.
Разброс по величине рH имеет место для тяжёлых дырок
в Ge и Si и электронов в InSb.
Рис. 2. Зависимость циклотронной массы электронов в Ge для магнитного поля H, лежащего в плоскости (110) кристалла, от угла q между H и осью [110], лежащей в той же плоскости (m0 - масса свободного электрона); T=4,2 K.
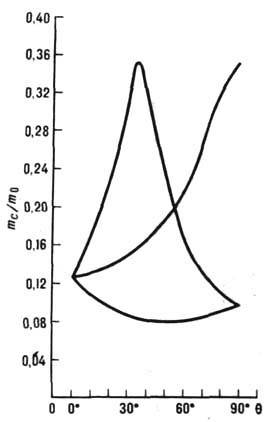
Рис. 3. Зависимость циклотронных масс дырок
в Ge при T= 4,2 К для поля H, лежащего в плоскости (110) кристалла
от угла q между H и осью [110].
На рис. 3 показана зависимость тс(q)для лёгких (скалярная эфф. масса) и тяжёлых дырок в Ge. Для последних
изоэнергетич. поверхности имеют сложную форму.
Для анизотропного закона дисперсии Ц. р.
возможен и при E(t)||H. Для неквадратичного закона дисперсии тс может
зависеть и от энергии 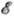 носителя.
носителя.
В классич. случае тс не зависит от величины H. В квантующем поле это справедливо только для сферич. или эллипсоидальной изоэнергетич. поверхностей. Для более сложных изоэнергетич. поверхностей спектр Ц. р. усложняется и тс может оказаться зависящей от H. Для вырожденных энергетич. зон возникает сложный неэквидистантный спектр уровней, вид которого существенно зависит не только от направления H, но и от величины рH.
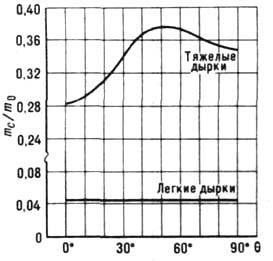
Определение знака заряда носителей. В
классич. Ц. р. вблизи резонанса |w -wс|t<=1
мощность P(w), поглощаемая в единице объёма полупроводника в плоскополяризованном
поле E(t), равна
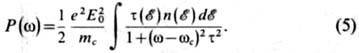
Здесь E0-амплитуда электрич.
поля, п(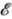 )-концентрация
носителей. Ф-ла (5) относится к случаю скалярной эфф. массы. В случае круговой
поляризации волны в зависимости от знака заряда носителя интенсивное поглощение
испытывает волна с правым или левым направлением вращения. На этом основан метод
определения знака заряда носителей.
)-концентрация
носителей. Ф-ла (5) относится к случаю скалярной эфф. массы. В случае круговой
поляризации волны в зависимости от знака заряда носителя интенсивное поглощение
испытывает волна с правым или левым направлением вращения. На этом основан метод
определения знака заряда носителей.
Форма и ширина линии. В случае классич.
Ц. р. полуширина dwc линии Ц. р., обусловленная
рассеянием, зависит от ср. энергии носителей 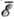 :
:

При низких темп-pax существенно рассеяние на
примесных атомах и акустич. фононах .Связь полуширины линии Ц. р. в единицах
магн. поля dH с обратным временем релаксации т-1
выражается соотношением
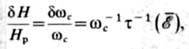
где Hp - значение H, отвечающее точному резонансу. В слабых электрич. полях (при отсутствии вырождения
носителей) ср. энергия носителей определяется распределением Больцмана: 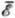 =(3/2)kT. В области низких T для легированного
полупроводника dН не зависит от температуры (рис. 4), что соответствует рассеянию на нейтральных
примесях. В области высоких температур dH
=(3/2)kT. В области низких T для легированного
полупроводника dН не зависит от температуры (рис. 4), что соответствует рассеянию на нейтральных
примесях. В области высоких температур dH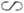 T 3/2, что отвечает рассеянию на акустич. фононах. Линия
классич. Ц. р. в слабых электрич. полях практически всегда имеет лоренцеву форму.
Площадь, огибаемая контуром спектральной линии Ц. р., содержит информацию о
концентрации носителей и, следовательно, об их времени жизни, если носители
не являются равновесными.
T 3/2, что отвечает рассеянию на акустич. фононах. Линия
классич. Ц. р. в слабых электрич. полях практически всегда имеет лоренцеву форму.
Площадь, огибаемая контуром спектральной линии Ц. р., содержит информацию о
концентрации носителей и, следовательно, об их времени жизни, если носители
не являются равновесными.
В случае сложных неэллипсоидальных изоэнергетич.
поверхностей наряду с уширением линии Ц. р. из-за процессов рассеяния (однородное
уширение) возникает также т. н. неоднородное уширение. связанное с зависимостью
тс от рH и 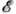 и с возникающим из-за этого разбросом wc (см. выше).
и с возникающим из-за этого разбросом wc (см. выше).
Ширина линии квантового Ц. р. Под действием
электрич. поля E(t) | H возникает суперпозиция
состояний нулевого и первого уровней. Это приводит к появлению плотности
тока в образце j(t) | H. Процессы затухания
(релаксации) этого тока и определяют ширину линии Ц. р. Если эту релаксацию
можно описать с помощью нек-рого эфф. времени релаксации, то выражение для поглощаемой
мощности (5) сохраняет силу. При этом под энергией следует понимать кинетич.
энергию движения носителей вдоль H, а под
п(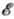 )
- концентрацию носителей на нулевом уровне. Время т можно ввести
для упругого рассеяния на примесных центрах и для рассеяния на акустич. фононах
в двух предельных случаях - квазиупругого рассеяния, если энергия акустич. фонона
(
)
- концентрацию носителей на нулевом уровне. Время т можно ввести
для упругого рассеяния на примесных центрах и для рассеяния на акустич. фононах
в двух предельных случаях - квазиупругого рассеяния, если энергия акустич. фонона
(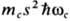 )1/2<<kT,
и неупругого рассеяния в случае >>kT(s-скорость звука).
В этом случае т -1 представляет собой полусумму обратных времён
жизни носителя в состояниях нулевого и первого уровней. Существ. вклад
в ширину линии квантового Ц. р. может давать уширение, связанное с изменением
энергетич. спектра носителей вследствие взаимодействия с рассеивателями.
)1/2<<kT,
и неупругого рассеяния в случае >>kT(s-скорость звука).
В этом случае т -1 представляет собой полусумму обратных времён
жизни носителя в состояниях нулевого и первого уровней. Существ. вклад
в ширину линии квантового Ц. р. может давать уширение, связанное с изменением
энергетич. спектра носителей вследствие взаимодействия с рассеивателями.
В двумерных системах - инверсионных слоях и квантовых ямах - в полях H. перпендикулярных плоскости
слоя, носители вследствие их высокой концентрации вырождены. Вид линии Ц. р.
в этих случаях зависит не только от величины уширений, но и от положения уровня
Ферми относительно уровней.
Гармоники Ц. р. В ряде случаев в спектрах
Ц. р. помимо резонансного поглощения на осн. частоте wс
наблюдаются также максимумы поглощения на частотах пwс
(п - целое число). В слабых полях (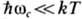 ) гармоники возникают при сложной (неэллипсоидальной) форме изоэнергетич. поверхностей.
В этом случае носители заряда в плоскости, перпендикулярной H,
движутся по сложной замкнутой кривой. Скорость электрона u
в этой плоскости не является уже простой гармонич. функцией времени t,
её разложение в ряд Фурье содержит наряду с частотой wc
кратные частоты пwс. Соответственно поглощаемая мощность P = euE
имеет на этих частотах максимумы. Гармоники Ц. р. для тяжёлых
дырок наблюдались в p-Ge и p-Si. При этом набор
гармоник зависит от ориентации H относительно кристаллографич. осей.
) гармоники возникают при сложной (неэллипсоидальной) форме изоэнергетич. поверхностей.
В этом случае носители заряда в плоскости, перпендикулярной H,
движутся по сложной замкнутой кривой. Скорость электрона u
в этой плоскости не является уже простой гармонич. функцией времени t,
её разложение в ряд Фурье содержит наряду с частотой wc
кратные частоты пwс. Соответственно поглощаемая мощность P = euE
имеет на этих частотах максимумы. Гармоники Ц. р. для тяжёлых
дырок наблюдались в p-Ge и p-Si. При этом набор
гармоник зависит от ориентации H относительно кристаллографич. осей.
В квантующем магн. поле и в слабом электрич.
поле E(t) | H переходы носителей происходят
только между соседними уровнями. Однако при одновременном воздействии
поля E(t)и поля рассеивателей оказываются разрешёнными
переходы между любыми уровнями. Это означает, что при 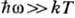 возникают переходы с нулевого уровня на уровни с n > 1 (хотя
вероятность таких переходов значительно меньше, чем переходов на примесях и
ак,устич. фононах), такие переходы происходят на частотах пwс и приводят к появлению гармоник (если же носители рассеиваются на оптич.
фононах, то имеет место циклотрон-фононный резонанс).
возникают переходы с нулевого уровня на уровни с n > 1 (хотя
вероятность таких переходов значительно меньше, чем переходов на примесях и
ак,устич. фононах), такие переходы происходят на частотах пwс и приводят к появлению гармоник (если же носители рассеиваются на оптич.
фононах, то имеет место циклотрон-фононный резонанс).
Разогрев носителей. T. к. высокочастотная
проводимость (для плоскополяризованной волны) на частоте wс
велика (она равна половине статич. проводимости), то в условиях Ц. р. возможен
разогрев носителей перем. полем. Этот метод используется для изучения рассеяния
на примесях и акустич. фононах. Осн. источником информации при этом является
соотношение 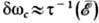 . При малой мощности W излучения ср. энергия носителей
. При малой мощности W излучения ср. энергия носителей  близка к равновесной. Если же W велико, то
близка к равновесной. Если же W велико, то 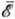 ,
а значит, и dwc, начинают зависеть от W.
,
а значит, и dwc, начинают зависеть от W.
При рассеянии на заряж. примесях т( )
- возрастающая функция, для акустич. фононов - убывающая, для нейтральных примесей
т слабо зависит от
)
- возрастающая функция, для акустич. фононов - убывающая, для нейтральных примесей
т слабо зависит от 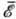 .
Поэтому в первом случае (а также при межэлектронном рассеянии)с ростом
.
Поэтому в первом случае (а также при межэлектронном рассеянии)с ростом
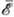 линия сужается, во втором - расширяется, в третьем- полуширина dwс
остаётся неизменной. С ростом
линия сужается, во втором - расширяется, в третьем- полуширина dwс
остаётся неизменной. С ростом 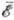 акустич. рассеяние становится преобладающим.
акустич. рассеяние становится преобладающим.
При разогреве в пост. электрич. поле E зависимость
т(E)определяется характером рассеяния. При умеренных значениях
E рассеяние обусловлено вынужденным взаимодействием с акустич. фононами
(т-1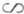 E0,5),
в сильных - спонтанной эмиссией фононов (т-1
E0,5),
в сильных - спонтанной эмиссией фононов (т-1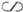 E0,8
) (см. Горячие электроны ).Такие же зависимости наблюдаются и от
амплитуды высокочастотного поля E0 в условиях Ц. p.
T. к. W
E0,8
) (см. Горячие электроны ).Такие же зависимости наблюдаются и от
амплитуды высокочастотного поля E0 в условиях Ц. p.
T. к. W E20, то dwc
E20, то dwc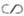 W0,25
в умеренном и dwc
W0,25
в умеренном и dwc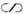 W0,4
в сильном высокочастотных полях.
W0,4
в сильном высокочастотных полях.
Разогрев носителей в высокочастотном поле имеет
два важных преимущества - отсутствие контактов в сильных электрич. полях и возможность
избирательного нагрева определ. группы носителей, напр. электронов одной долины
зоны проводимости в многодолинных, полупроводниках.
Экспериментальные методы. Существуют 2
осн. способа наблюдения Ц. р. Первый состоит в измерении поглощения эл--магн.
мощности. Второй способ использует то обстоятельство, что поглощение излучения
приводит к возрастанию энергии носителей. Это, в свою очередь, приводит к изменению
проводимости s полупроводника на пост. токе. Зависимость изменения Ds
от w или от H воспроизводит линию Ц. р. Этот способ имеет то преимущество,
что детектором является сам образец. Кроме того, обычно этот способ оказывается
более чувствительным, чем измерение поглощения. Однако в тех редких случаях,
когда в пределах резонансной линии возникает смена механизма рассеяния (а), смена механизма рекомбинации носителей (б)или изменение типа проводимости
(в), то кривая Ds(w) или Ds(H) в случаях
(а)и (б)становится двугорбой, а в случае (в) функция Ds(H)напоминает закон дисперсии показателя преломления.
В спектрометрах Ц. р. в качестве генераторов
эл--магн. излучения в сантиметровом диапазоне длин волн используются клистроны, генераторы Ганна (см. Ганна диод)и лавинно-пролётные диоды, в
миллиметровом и субмиллиметровом диапазонах - лампы обратной волны, в
субмиллиметровом и ИК-диапазонах - лазеры. Источниками магн. поля, как правило,
служат сверхпроводящие соленоиды (H~100 кЭ). Свободные носители заряда
в полупроводниках при низких темп-pax создаются подсветкой. Для увеличения чувствительности
применяются модуляц. методы регистрации (изменение концентрации свободных носителей
при изменении интенсивности света). В связи с низкой добротностью линий Ц. р.
обычно применяется развёртка спектров вариацией поля H.
Циклотронный резонанс в металлах
Исследование Ц. р. в металлах имеет большое значение
для теории металлов. Он позволяет определить форму и размеры ферми-поверхности.
времена свободного пробега носителей, электрон-фононное взаимодействие и др.
В металлах эл--магн. волны почти полностью отражаются
от поверхности образца, проникая в металл на небольшую глубину скин-слоя d~10-5
см (см. Скин-эффект ).В хороших металлах, где число электронов - 1/атом,
d~10-5-10-6 см; в полуметаллах (напр., у Bi)
d ~ 10 -4см. Радиус ларморовской орбиты электронов r, обратно
пропорциональный полю H, сравним с d лишь в сильных полях Н~ 106-107 Э (для полуметаллов Н~ 104 Э).
В обычных же магн. полях эл--магн. поле взаимодействует с электронами лишь на
малом участке их орбиты. В результате электроны проводимости движутся в сильно
неоднородном эл--магн. поле, поскольку, как правило, диаметр их орбиты 2r>>
d. Если магн. поле параллельно поверхности образца, то среди электронов
есть такие, к-рые, хотя и движутся большую часть времени в глубине металла,
где электрич. поля нет, однако на короткое время заходят в скин-слой, где взаимодействуют
с волной (рис. 5).
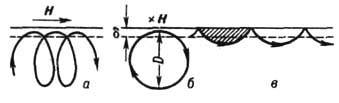
Рис. 5. Траектории электронов: а, б-в однородном
постоянном магнитном поле H при действии
переменного электрического поля E
| H; магнитное поле H направлено
параллельно поверхности металла; в- зеркально,
отражающихся от поверхности металла.
Механизм передачи энергии от волны носителям
в этом случае аналогичен работе циклотрона ,резонанс возникает, если
электрон будет попадать в скин-слой каждый раз при одной и той же фазе электрич.
поля, что возможно при w=
пwс
= пеН/тсс. Это условие отвечает резонансам, периодически повторяющимся
при изменении 1/H. Электрон возвращается в ускоряющий слой через один
или неск. периодов перем. поля T=2p/w, каждый раз получая энергию
от поля.
В случае поля H, наклонного
относительно поверхности образца, электроны, проходя по направлению поля H
за один оборот путь порядка r, проводят в слое d время, равное
(2p/w) (d/r) <= 2pw. При этом периодичность движения
в поле H на их взаимодействие с перем. полем не влияет,
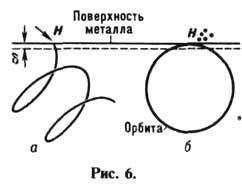
и Ц. р. отсутствует (рис. 6, а).
Приведённое описание является исчерпывающим только
в случае электронов с квадратичным законом дисперсии, когда тс, а следовательно, и wс
одинаковы для всех электронов. В случае более сложных законов дисперсии
wc
как и в случае полупроводников, может зависеть от 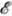 и рH. При этом
для Ц. р. существенны только электроны с энергией
и рH. При этом
для Ц. р. существенны только электроны с энергией 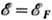 (
( -ферми-энергия). Из электронов с разл. pH, образующими непрерывный
спектр циклотронных частот wc, осн. роль в Ц. р. играют:
1) электроны вблизи экстремальных значений pHextr на
ферми-поверХности
-ферми-энергия). Из электронов с разл. pH, образующими непрерывный
спектр циклотронных частот wc, осн. роль в Ц. р. играют:
1) электроны вблизи экстремальных значений pHextr на
ферми-поверХности 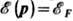 , где wc(pH)медленнее всего меняется, а плотность состояний электронов, как функция wс,
обращается в бесконечность; 2) электроны вблизи особых точек - граница спектра
wс(рHгр).
, где wc(pH)медленнее всего меняется, а плотность состояний электронов, как функция wс,
обращается в бесконечность; 2) электроны вблизи особых точек - граница спектра
wс(рHгр).
Измерение частот Ц. р. позволяет непосредственно
определить экстремальные и граничные значения тс. Полуширина
резонансной линии определяет время свободного
пробега т, к-рое в условиях Ц. р. (d<<r, wт
>> 1) может быть введено в металлах. Возможность введения т связана
с тем. что основную роль в Ц. р. играет малая часть электронов вблизи экстремальных
и граничных значений рH и с малой проекцией скорости
на нормаль к поверхности металла. Возможен лишь "уход" из этих состояний
во все остальные ("приходом" электронов в эту узкую область значений
рH из-за случайных столкновений можно пренебречь).
В результате т при Ц. р. может существенно отличаться от статич. т.
Так, напр.. в статич. случае однократное столкновение электрона с фононом слабо
рассеивает электрон и малосущественно; существенным становится лишь число столкновений
порядка (QД/T)2,
где QД
- Дебая температура ,tэф~T -5. При Ц. р. уже однократное столкновение с фононом может вывести
электрон из ускоряющего слоя или из "резонансного" рH, т. е. оказаться существенным, что обусловливает трезэф~Т -3.
Исследование Ц. р. в пластинках тоньше длины
свободного пробега электронов позволяет выяснить, какая из электронных орбит
последней помещается в пластинке и даёт Ц. р. (радиус орбиты пропорционален
1/Н, следовательно, номеру и резонансной гармоники). При большом n это (с относит. точностью ~n-1) определяет диаметр поверхности
Ферми в соответствующем направлении. Ц. р. может дать также информацию и об
открытых траекториях электронов, если их направление параллельно поверхности
образца (см. Ферми-поверхность).
Поверхностный импеданс в условиях Ц. р. Комплексная
проводимость. В металлах характеристики Ц. р. удобно выражать через
поверхностный импеданс:
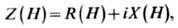
где R - активное, X-реактивное
сопротивления. Резонансное значение полного поверхностного импеданса Z связано
с временем свободного пробега электрона т и частотой излучения w
следующими ф-лами: 1) в случае квадратичного закона дисперсии:
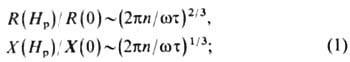
2) для произвольного закона дисперсии при максимальной
тс и минимальной wc:
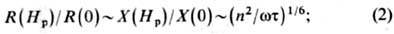
3) в случае минимальной тс:
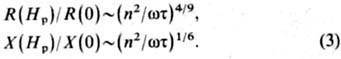
При Ц. р. ток при заданной напряжённости электрич.
поля максимален, что соответствует минимумам R и X. Полуширина
резонансной линии Dwc~2pn/wт.
Отсюда и из ф-л (1) - (3) следует, что вещественная и мнимая части дZ/дH при Ц. р. максимальны.
Комплексная проводимость s в простейшем
случае квадратичного изотропного закона дисперсии носителей и взаимноперпендикулярных
E и H равна
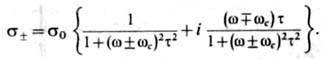
Здесь s0-статич. проводимость
кристалла в отсутствие магн. поля. T. о., sb отличается
от s0 лишь заменой 1/т на 1/т + i(wbwc).
Это естественно, т. к. действие H на электронный газ эквивалентно
вращению его как целого с частотой wс.
Магнитные поверхностные уровни. В металлах в тех же условиях, что и Ц. р., может наблюдаться близкое к нему по природе явление-осцилляции поверхностей проводимости из-за квантовых переходов между магнитными поверхностными уровнями. Они возникают, если электроны могут зеркально отражаться от поверхности образца, совершая тем самым периодич. движение, к-рое квантовано, и разрешёнными оказываются такие орбиты, для к-рых поток магн. поля через сегмент, образуемый дугой траектории и поверхностью образца, равен (п+ 1/4)ch/e.

|
|