 на электрические
свойства проводников (металлов,
полупроводников, полуметаллов), по которым протекает электрический ток
(плотностью
на электрические
свойства проводников (металлов,
полупроводников, полуметаллов), по которым протекает электрический ток
(плотностью 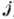 ).
).
 на электрические
свойства проводников (металлов,
полупроводников, полуметаллов), по которым протекает электрический ток
(плотностью
на электрические
свойства проводников (металлов,
полупроводников, полуметаллов), по которым протекает электрический ток
(плотностью 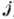 ).
).
Различают нечётные гальваномагнитные явления, характеристики которых меняют
знак при изменении направления 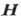 на обратное, и чётные (не меняют знак), а также
продольные (
на обратное, и чётные (не меняют знак), а также
продольные (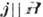 )
и поперечные (
)
и поперечные (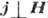 _ ).
Наиболее важные гальваномагнитные явления из нечётных - Холла эффект - возникновение разности
потенциалов в направлении, перпендикулярном
_ ).
Наиболее важные гальваномагнитные явления из нечётных - Холла эффект - возникновение разности
потенциалов в направлении, перпендикулярном 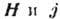 ;
из чётных - изменение удельного сопротивления р при
;
из чётных - изменение удельного сопротивления р при 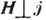 (поперечное магнетосопротивление). При сравнительно небольших плотностях
тока, когда справедлив закон Ома, т. е. между напряжённостью электрич. поля
(поперечное магнетосопротивление). При сравнительно небольших плотностях
тока, когда справедлив закон Ома, т. е. между напряжённостью электрич. поля
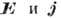 есть линейная
связь (в общем случае анизотропная),
есть линейная
связь (в общем случае анизотропная),
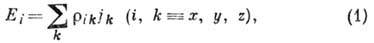
Гальваномагнитные явления определяются зависимостью
от 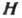 компонент тензора
удельных сопротивлений
компонент тензора
удельных сопротивлений
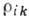 .
.
Влияние магн. поля приводит к изменению джоулева тепла Q, выделяющегося
в кристалле, и к появлению добавочного, отсутствующего при  электрич. поля (поля Xолла)
электрич. поля (поля Xолла) 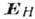 .
Величины
.
Величины 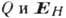 определяются
соответственно симметричной и антисимметричной частями тензора
определяются
соответственно симметричной и антисимметричной частями тензора 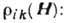
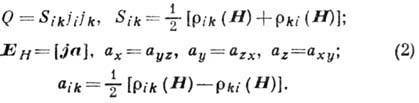
Разность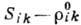 , где
, где 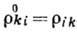 при Н=0,
наз. тензором магнетосопротивлений, а скалярная величина
при Н=0,
наз. тензором магнетосопротивлений, а скалярная величина 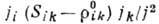 -
магнетосопротивлением, причём в качестве характеристики изменения сопротивления
в магн. поле принимают отношение
-
магнетосопротивлением, причём в качестве характеристики изменения сопротивления
в магн. поле принимают отношение
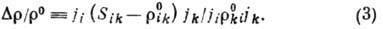
Оно зависит от величины
и направления 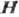 ,
а также от направления
,
а также от направления 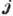 .
Согласно принципу симметрии, кинетич. коэф. Онсагера (см. Онсагера теорема)
.
Согласно принципу симметрии, кинетич. коэф. Онсагера (см. Онсагера теорема)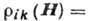
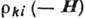 , из-за
чего компоненты тензора
, из-за
чего компоненты тензора 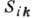 -чётные
функции
-чётные
функции 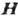 , а компоненты
вектора
, а компоненты
вектора 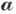 -нечётные,
т. е. тензор
-нечётные,
т. е. тензор 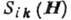 описывает чётные гальваномагнитные явления, а вектор
описывает чётные гальваномагнитные явления, а вектор 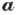 -
нечётные.
-
нечётные.
Зависимость 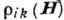 обусловлена влиянием магн. поля на траектории носителей заряда (для определённости
электронов). При H=0 электрон между столкновениями с фононами или
дефектами кристаллич. решётки движется прямолинейно,
при
обусловлена влиянием магн. поля на траектории носителей заряда (для определённости
электронов). При H=0 электрон между столкновениями с фононами или
дефектами кристаллич. решётки движется прямолинейно,
при 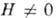 его путь
искривляется. Грубой оценкой кривизны траектории может служить Ларморовский
радиус
его путь
искривляется. Грубой оценкой кривизны траектории может служить Ларморовский
радиус 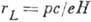 , где р - импульс, е -заряд электрона. При этом мерой влияния H должно
служить отношение длины свободного пробега l электрона к
, где р - импульс, е -заряд электрона. При этом мерой влияния H должно
служить отношение длины свободного пробега l электрона к 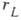 ,
а
,
а 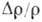 должно быть
функцией
должно быть
функцией 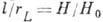 . Величина
. Величина
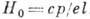 , при к-рой
, при к-рой  ,
разделяет все магн. поля на слабые
,
разделяет все магн. поля на слабые 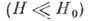 и сильные
и сильные  . Для
полупроводников принято выражать
. Для
полупроводников принято выражать 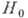 через подвижность носителей заряда
через подвижность носителей заряда 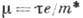 (
(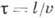 -транспортное
время свободного пробега,
-транспортное
время свободного пробега, 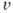 -скорость
электрона,
-скорость
электрона,  -
его эффективная масса:)
-
его эффективная масса:)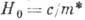
Величина H0 зависит от температуры T: с понижением T 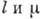 возрастают, а
возрастают, а 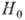 уменьшается. Если при Т~300 К для разл. металлов и хорошо проводящих
полупроводников Н0~105-107 Э (для Bi
Н0~104 Э), а для плохо проводящих полупроводников
H0 ~108-109 Э, то при низких темп-pax
ограничение для H0 , как правило, накладывает чистота образца.
Для предельно чистых образцов (Bi, W,Sn) при Т~4 К Н0~102
О. Уменьшение H0 с температурой позволяет, используя обычные поля
~104- 105 Э, осуществить условия, соответствующие сильному
полю.
уменьшается. Если при Т~300 К для разл. металлов и хорошо проводящих
полупроводников Н0~105-107 Э (для Bi
Н0~104 Э), а для плохо проводящих полупроводников
H0 ~108-109 Э, то при низких темп-pax
ограничение для H0 , как правило, накладывает чистота образца.
Для предельно чистых образцов (Bi, W,Sn) при Т~4 К Н0~102
О. Уменьшение H0 с температурой позволяет, используя обычные поля
~104- 105 Э, осуществить условия, соответствующие сильному
полю.
Если в плоскости, перпендикулярной 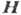 , электрон совершает периодическое (финитное) движение,
то его энергия квантуется, причём расстояние между уровнями энергии равно
, электрон совершает периодическое (финитное) движение,
то его энергия квантуется, причём расстояние между уровнями энергии равно
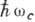 ,
где
,
где 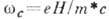 - циклотронная
частота. Квантование движения электронов проявляется в гальваномагнитных явлениях только в том
случае, если
- циклотронная
частота. Квантование движения электронов проявляется в гальваномагнитных явлениях только в том
случае, если 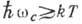 .
Магнитные поля, удовлетворяющие условию
.
Магнитные поля, удовлетворяющие условию 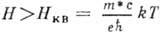 , наз. квантующими. Обычно при Т~300 К
, наз. квантующими. Обычно при Т~300 К 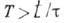 и В
и В 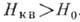 полупроводниках и полуметаллах концентрация носителей мала, и при низких темп-pax
удаётся реализовать случай, когда заполнен лишь один магн. уровень (т. н. квантовый
предел:
полупроводниках и полуметаллах концентрация носителей мала, и при низких темп-pax
удаётся реализовать случай, когда заполнен лишь один магн. уровень (т. н. квантовый
предел: 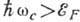 , где
, где
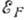 -энергия Ферми
вырожденного проводника при H=0).
-энергия Ферми
вырожденного проводника при H=0).
В слабых магнитных полях 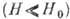 можно воспользоваться разложением
можно воспользоваться разложением 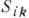 и
аi по степеням
и
аi по степеням 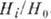 Учитывай чётность
Учитывай чётность 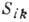 и нечётность аi, имеем:
и нечётность аi, имеем:
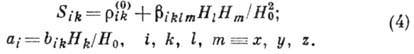
Здесь 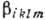 -тензор 4-го ранга, симметричный как по индексам i и k, так и
по l и т (
-тензор 4-го ранга, симметричный как по индексам i и k, так и
по l и т (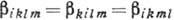 ) (принцип Онсагера не требует симметрии тензора bik)). Порядок
величины компонент тензоров
) (принцип Онсагера не требует симметрии тензора bik)). Порядок
величины компонент тензоров 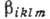 и
и 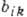 определяется
значением удельного сопротивления r0 при H=0 (
определяется
значением удельного сопротивления r0 при H=0 (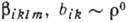 ). Т.о., при
). Т.о., при 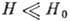 магнетосопротивление (а значит, и Q)квадратично зависит от H, а
поле Холла
магнетосопротивление (а значит, и Q)квадратично зависит от H, а
поле Холла 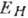 -линейно.
Численные значения компонент
-линейно.
Численные значения компонент 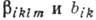 определяются параметрами рассеяния электронов и могут быть вычислены только
с использованием конкретных предположений о рассеянии носителей заряда в
твёрдом теле. Однако число независимых компонент этих тензоров (анизотропия
гальваномагнитных явлений в слабых полях) не зависит от механизмов рассеяния, а только от симметрии
кристалла.
определяются параметрами рассеяния электронов и могут быть вычислены только
с использованием конкретных предположений о рассеянии носителей заряда в
твёрдом теле. Однако число независимых компонент этих тензоров (анизотропия
гальваномагнитных явлений в слабых полях) не зависит от механизмов рассеяния, а только от симметрии
кристалла.
Для изотропных проводников (поликристаллов) тензор удельных сопротивлений изотропен:
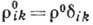 (
(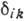 -символ Кронекера),
-символ Кронекера),
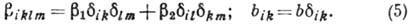
При 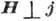 :
:
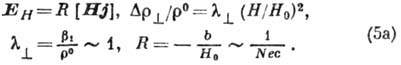
При 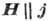 эффект Холла отсутствует, а
эффект Холла отсутствует, а
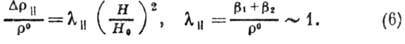
Величина R носит
назв. коэф. Холла, для её оценки использована Друде формула 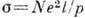 , где N - концентрация электронов,
, где N - концентрация электронов, 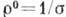 (дальше просто
(дальше просто 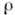 ).
При T
).
При T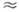 300
К обычно
300
К обычно 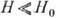 и можно
пользоваться ф-лами (5) и (6). Исключение составляет Bi, у к-рого при Н
и можно
пользоваться ф-лами (5) и (6). Исключение составляет Bi, у к-рого при Н 3*104
Э
3*104
Э 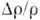 велико (~2).
Это дает возможность использовать Bi для измерения магнитных полей.
велико (~2).
Это дает возможность использовать Bi для измерения магнитных полей.
Анализ эксперим зависимости 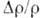 металлов от Н у разл проводников разной
степени чистоты при разл. T привел к обнаружению правила Колера, согласно к-рому
металлов от Н у разл проводников разной
степени чистоты при разл. T привел к обнаружению правила Колера, согласно к-рому 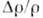 металла - функция
металла - функция 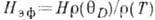 ,
где
,
где 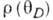 - сопротивление
(при Н=0) данного металла при Дебая температуре
- сопротивление
(при Н=0) данного металла при Дебая температуре 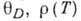 - сопротивление (при H=O)определ. образца при температуре T. Величина
- сопротивление (при H=O)определ. образца при температуре T. Величина
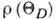 практически не
изменяется при переходе от образца к образцу данного металла, т. к. определяется
рассеянием электронов на фононах,
практически не
изменяется при переходе от образца к образцу данного металла, т. к. определяется
рассеянием электронов на фононах, 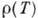 при
при 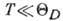 существенно
зависит от состояния образца - от его чистоты, наличия или отсутствия дефектов,
в т. ч. дислокаций (рис. 1).
существенно
зависит от состояния образца - от его чистоты, наличия или отсутствия дефектов,
в т. ч. дислокаций (рис. 1).
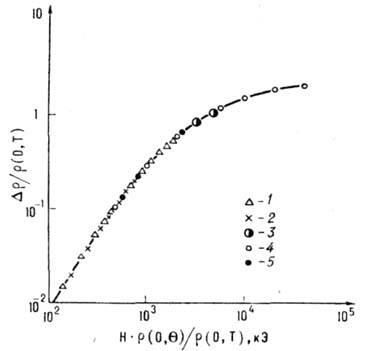
Рис. 1. Магнетосопротивление
поликристаллического In в поперечном магнитном поле для трех образцов при различной
температуре 1) Т=14К, 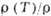 (273) = 0,24 2) Т=14 К,
(273) = 0,24 2) Т=14 К, 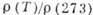 = 0,0086 3) Т = 4,2 К,
= 0,0086 3) Т = 4,2 К, 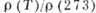 =0,0012
4) T=4,2К,
=0,0012
4) T=4,2К, 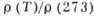 = 0,00007,
5) Т=2К,
= 0,00007,
5) Т=2К,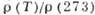 =0,00003
(
=0,00003
(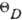 =120К)
=120К)
Правило Колера, сформулированное
для поликристаллич. образцов металлов, подтверждает представление о том, что
гальваномагнитные явления обусловлены искривлением траектории электронов в магн поле, т. к Нэф отличается от 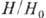 постоянным для данного металла множителем
постоянным для данного металла множителем
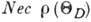
Металлы. Исследования при низких темп-pax монокристаллич. образцов металлов
в 1940-50-е гг. [E. Юсти (E. Justi), E. С. Боровик, H. E. Алексеевский, Ю. П.
Гайдуков], позволившие осуществить условие 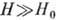 , обнаружили разнообразные зависимости
, обнаружили разнообразные зависимости 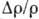 от величины и направления H у разл. металлов. При
от величины и направления H у разл. металлов. При 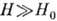 гальваномагнитные явления зависят от электронной энергетич. структуры металлов, в частности от формы
ферми-поверхности (напр., открытая или замкнутая, рис 2).
гальваномагнитные явления зависят от электронной энергетич. структуры металлов, в частности от формы
ферми-поверхности (напр., открытая или замкнутая, рис 2).
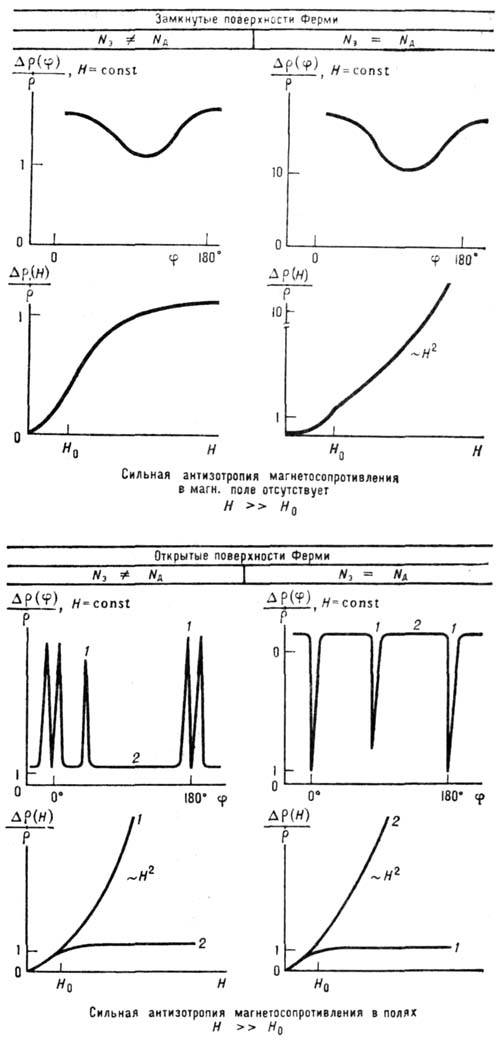
Рис. 2. Схематическое изображение
зависимости поперечного магнетосопротнвления 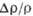 от величины и направления магнитного поля H для металлов с разной
геометрией поверхности Ферми:
от величины и направления магнитного поля H для металлов с разной
геометрией поверхности Ферми: 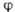 -
угол, задающий направление H относительно кристаллографич. осей,
1 - направления, для к-рых существуют открытые траектории электронов
2 - направления где все траектории - замкнутые линии NЭ -
концентрация электронов проводимости, NД - дырок
-
угол, задающий направление H относительно кристаллографич. осей,
1 - направления, для к-рых существуют открытые траектории электронов
2 - направления где все траектории - замкнутые линии NЭ -
концентрация электронов проводимости, NД - дырок
Вырождение электронного газа выделяет среди всех электронов металла электроны
с энергией, равной энергии Ферми, т. е. расположенные в пространстве квазиимпульсов
на поверхности Ферми. T. к. при движении в магн. поле сохраняются энергия электрона
и проекция его
квазиимпульса на Н, то под действием силы Лоренца электроны
движутся по поверхности Ферми. Траектория электрона на поверхности Ферми - кривая,
расположенная на плоскости, перпендикулярной Н. В зависимости от топологии
поверхности Ферми траектория может быть замкнутой, а может уходить в бесконечность
(рис. 3). Траектория электрона в реальном пространстве (в плоскости, перпендикулярной
Н)подобна его траектории на поверхности Ферми. Поэтому
зависимость поперечных (относительно H) компонент тензора
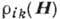 определяется топологией поверхности Ферми. Эта зависимость, естественно, проявляется
тем четче, чем больше H отличается от Н0, т. е. чем
больше времени до столкновения электрон движется по определ. траектории (при
определяется топологией поверхности Ферми. Эта зависимость, естественно, проявляется
тем четче, чем больше H отличается от Н0, т. е. чем
больше времени до столкновения электрон движется по определ. траектории (при
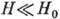 он вовсе не успевает
"выписать" траекторию и его движение между
столкновениями можно считать прямолинейным). Если поверхность Ферми замкнута,
то траектории всех электронов тоже замкнуты. При
он вовсе не успевает
"выписать" траекторию и его движение между
столкновениями можно считать прямолинейным). Если поверхность Ферми замкнута,
то траектории всех электронов тоже замкнуты. При 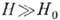 перемещение электронов в плоскости, перпендикулярной H, осуществляется
за счет столкновений, в результате которых электрон "перепрыгивает"
с орбиты на орбиту; его поперечная проводимость при этом
перемещение электронов в плоскости, перпендикулярной H, осуществляется
за счет столкновений, в результате которых электрон "перепрыгивает"
с орбиты на орбиту; его поперечная проводимость при этом 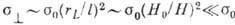 . Если поверхность Ферми открытая, то характер траектории зависит от направления
H; есть направления, при к-рых траектория открыта, а перемещение
электрона вдоль них, как и при Н=0, ограничено длиной свободного
пробега (проводимость в этом направлении
. Если поверхность Ферми открытая, то характер траектории зависит от направления
H; есть направления, при к-рых траектория открыта, а перемещение
электрона вдоль них, как и при Н=0, ограничено длиной свободного
пробега (проводимость в этом направлении 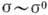 ). Это - причина резкой анизотропии сопротивления у металлов с открытыми поверхностями
Ферми.
). Это - причина резкой анизотропии сопротивления у металлов с открытыми поверхностями
Ферми.
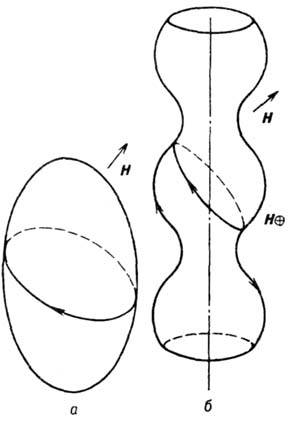
Рис. 3. Примеры траекторий
электронов в пространстве квазиимпульсов: а- на замкнутой поверхности
Ферми траектории при любом направлении Н замкнуты; б -
на открытой поверхности Ферми при одних направлениях Н они замкнуты,
при других - открыты.
Различие в поведении скомпенсированных
(концентрации электронов проводимости N3 и дырок NД равны) и нескомпенсированных 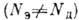 металлов объясняется разл. ролью холловских компонент тензора проводимости
металлов объясняется разл. ролью холловских компонент тензора проводимости 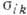 . Рассмотрим для примера модельный (воображаемый) металл с двумя группами
носителей: электроны и дырки заполняют сферич. поверхности Ферми. Связь между
. Рассмотрим для примера модельный (воображаемый) металл с двумя группами
носителей: электроны и дырки заполняют сферич. поверхности Ферми. Связь между
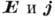 задаётся в этой
модели уравнениями:
задаётся в этой
модели уравнениями:
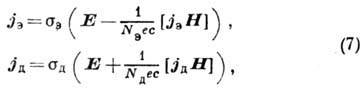
где 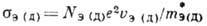 (е > 0,
(е > 0, 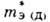 >
0; знак эффективной массы дырки учтён в ур-нии для
>
0; знак эффективной массы дырки учтён в ур-нии для 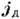 ).
Из ур-ний (7) можно определить компоненты тензора электропроводности металла
(ось
).
Из ур-ний (7) можно определить компоненты тензора электропроводности металла
(ось 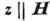 ):
):
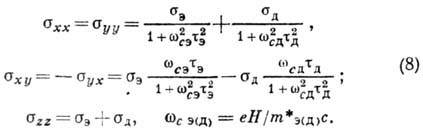
С ростом Н все поперечные
компоненты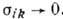 . Однако
асимптотика поперечных компонент тензора
. Однако
асимптотика поперечных компонент тензора 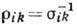 зависит от соотношения между диссипативными ( sxx,
зависит от соотношения между диссипативными ( sxx,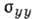 ) и холловскими
) и холловскими 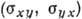 компонентами. Действительно,
компонентами. Действительно,
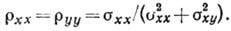
При одном сорте носителей
зависимость 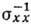 от
H полностью компенсируется холловским множителем
от
H полностью компенсируется холловским множителем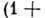
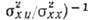 и
и 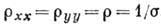 . При этом
коэф. Холла
. При этом
коэф. Холла

Причина независимости сопротивления
от Н 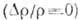 и
универсального характера ф-лы (9) - в отсутствие дисперсии носителей заряда.
Учет неполного вырождения носителей и зависимости t от энергии приводит к отличию
R от (9) и
и
универсального характера ф-лы (9) - в отсутствие дисперсии носителей заряда.
Учет неполного вырождения носителей и зависимости t от энергии приводит к отличию
R от (9) и 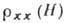 от r.
от r.
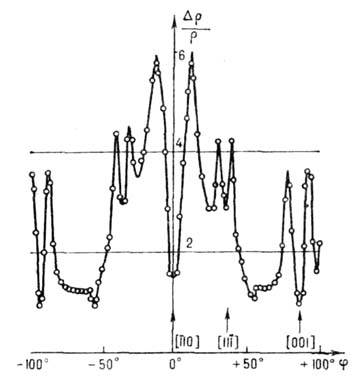
Рис. 4. Зависимость 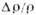 монокристалла Au от угла
монокристалла Au от угла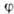 ,
задающего направление H, при Т = 4,2К.
,
задающего направление H, при Т = 4,2К. 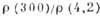 =1650,
H0=1,5 кЭ, Н = 23,5 кЭ.
=1650,
H0=1,5 кЭ, Н = 23,5 кЭ.
В случае двух сортов носителей,
согласно (8), при больших полях (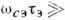 1,
1, 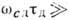 1):
1):
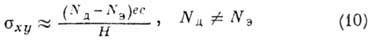
и
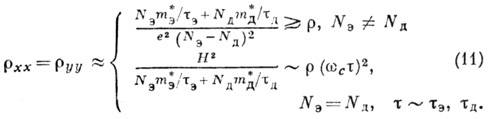
Постоянная Холла 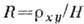 ; при
; при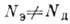 в сильных
полях:
в сильных
полях:
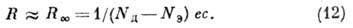
Ф-ла (12), зависимость
от Н и оценка порядка величины в ф-ле (11), полученные для простой модели,
сохраняются для металлов с замкнутыми поверхностями Ферми произвольной формы.
Кроме того, результаты не зависят от характера диссипативных процессов.
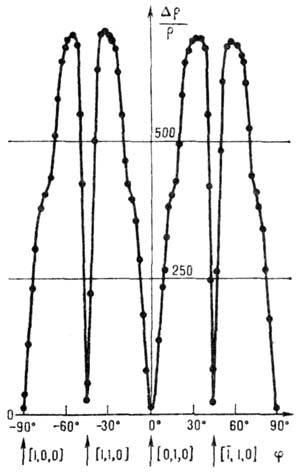
Рис. 5. Зависимость магнетосопротивления
монокристалла Sn от угла j, задающего Н, при Т =
4,2К,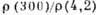 = 10,4, Н
= 23,5 кЭ; ток течёт вдоль оси [001], поле вращается в плоскости (001).
= 10,4, Н
= 23,5 кЭ; ток течёт вдоль оси [001], поле вращается в плоскости (001).
У большинства металлов
поверхности Ферми сложны (имеют открытые и замкнутые полости), разные группы
электронов имеют разные l. Это усложняет зависимость от Н в полях
и даёт возможность
использовать гальваномагнитные явления
как метод исследования электронного спектра и процессов рассеяния. Эффекты,
обусловленные формой траекторий электронов, практически не проявляются в продольном
сопротивлении; для всех металлов, как правило, 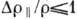 , даже при
, даже при 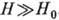
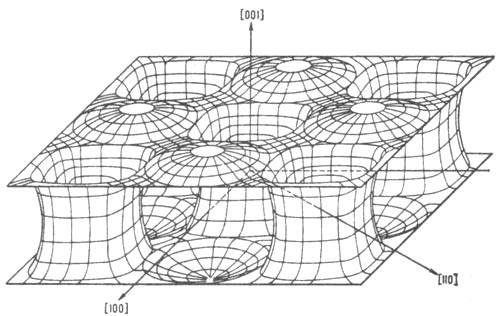
Рис. 6. Контуры открытой
поверхности Ферми Sn, восстановленные по набору кривых, подобных рис. 5.
Чувствительность характеристик
гальваномагнитных явлений при 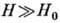 к структуре
электронного спектра позволила использовать эксперим. зависимости поперечного
сопротивления металлич. монокристаллов от величины и направления H
(рис. 4, 5) для определения их поверхностей Ферми. При этом оказалось, что большинство
металлов имеет открытые поверхности Ферми (Au, Ag, Cu, Sn, Pb; рис. 6), a Na,
К, Rb, Al, In, а также полуметаллы (Bi, Sb) - замкнутые. Одновременно выяснилось,
что Капицы закон - следствие усреднения
к структуре
электронного спектра позволила использовать эксперим. зависимости поперечного
сопротивления металлич. монокристаллов от величины и направления H
(рис. 4, 5) для определения их поверхностей Ферми. При этом оказалось, что большинство
металлов имеет открытые поверхности Ферми (Au, Ag, Cu, Sn, Pb; рис. 6), a Na,
К, Rb, Al, In, а также полуметаллы (Bi, Sb) - замкнутые. Одновременно выяснилось,
что Капицы закон - следствие усреднения 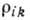 (Н)по кристаллитам для металлов с открытыми поверхностями Ферми
и переходная область от
(Н)по кристаллитам для металлов с открытыми поверхностями Ферми
и переходная область от 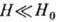 к
к 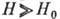 для металлов
с замкнутыми поверхностями Ферми.
для металлов
с замкнутыми поверхностями Ферми.
В гальваномагнитных явлениях важную роль играет
рассеяние электронов поверхностью образца: если траектория электронов замкнута,
то поперечная проводимость осуществляется путём столкновений. Поэтому поверхностное
рассеяние приводит к увеличению проводимости в приповерхностном слое, что находит
отражение в зависимости 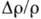 от Н для образцов конечных размеров (статический скин-эффект, см. также Размерные эффекты).
от Н для образцов конечных размеров (статический скин-эффект, см. также Размерные эффекты).
В сильных (квантующих) магнитных полях проявляет себя квантование энергии
электронов, движущихся
по замкнутым орбитам (см. выше). В металлах и вырожденных полупроводниках наблюдаются
осцилляции магнетосопротивления в зависимости от поля Н (Шубникова
- де Гааза эффект). Так же как и де Гааза - ван Альфена эффект, он обусловлен
осцилляциями в зависимости от 1/H плотности состояний электронов на границе
Ферми (см. Квантовые осцилля-ии в магнитном поле). Для типичных металлов
осцилляционная зависимость обычно имеет малую амплитуду и "накладывается"
на плавную "классическую", существенно не деформируя последнюю (рис.
7).
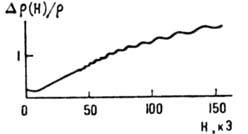
Рис. 7. Осцилляции Шубникова
- де Гааза малой амплитуды на фоне слабого монотонного роста магнетосопротивления
монокристалла Со при Т=4,2 К.
Изменение (по сравнению
с классическими) зависимостей 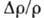 и
и 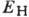 от Н
может быть обязано также магнитному пробою (туннельному проникновению
электронов с одной траектории на другую при определённых направлениях Н).
В частности, магнитный пробой может
быть источником осцилляции
от Н
может быть обязано также магнитному пробою (туннельному проникновению
электронов с одной траектории на другую при определённых направлениях Н).
В частности, магнитный пробой может
быть источником осцилляции  большой амплитуды (рис. 8).
большой амплитуды (рис. 8).
Своеобразные квантовые
эффекты, обусловленные интерференцией электронных волн, прошедших разные пути,
приводят к аномальному магнетосопротивлению, проявляющемуся в слабых
магн. полях. Аномальное магнетосопротивление подавляется неупругим рассеянием,
рассеянием с переворотом спина и др.
Рис. 8. Магнетопробойные
осцилляции в монокристалле Be при Т = 2 К.
Ферро- и антиферромагн.
металлы обладают аномальными гальваномагн. свойствами в полях 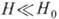 (см. Ферромагнетизм, Антиферромагнетизм). При
(см. Ферромагнетизм, Антиферромагнетизм). При 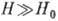 их поведение такое, как и поведение других металлов. Гальваномагнитные явления. в сплавах и интерметаллических
соединениях не отличаются существенно от гальваномагнитных явлений в простых металлах.
их поведение такое, как и поведение других металлов. Гальваномагнитные явления. в сплавах и интерметаллических
соединениях не отличаются существенно от гальваномагнитных явлений в простых металлах.
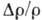 от H, обязанная классич. движению электронов в магнитном поле (рис. 9).
от H, обязанная классич. движению электронов в магнитном поле (рис. 9).
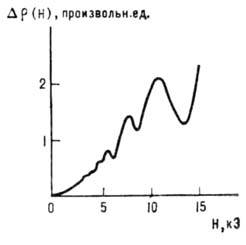
Рис. 9. Осцилляции Шубникова
- де Гааза в монокристалле Bi при Г=1,5 К.
|
Характеристики
гальваномагнитных явлений в полупроводниках при некоторых механизмах
рассеяния |
||||||||||
|
Механизм рассеяния |
Неквантующее магнитное
поле |
Квантовый предел |
||||||||
|
|
|
|
|
|
|
|||||
|
невырожденный полупроводник |
вырожденный полупроводник |
невырожденный полупроводник |
вырожденный полупроводник |
|||||||
|
Ионизированные
примеси |
1,5 |
1,93 |
2,15 |
0,706 |
H0T3/2 |
H3T° |
H0T3/2 |
Н3Т |
||
|
Акустические фононы
(деформационное взаимодействие) |
-0,5 |
1, 18 |
0,38 |
0,116 |
H2T-1/2 |
H5T |
HT1/2 |
H2T |
||
|
Акустические фононы
(пьезоэлектрическое взаимодействие) |
0,5 |
1,10 |
0,89 |
0,116 |
HT-1/2 |
Н4Т |
H0T1/2 |
HT |
||
Гальваномагнитные явления в
полупроводниках обладают рядом особенностей, обусловленных прежде всего
малой концентрацией носителей заряда. Электронно-дырочный газ полупроводников
при T~300 K невырожден, и характеристики гальваномагнитных явлений существенно зависят от
механизма рассеяния носителей (табл.). Выяснение роли разл. механизмов рассеяния
- одна из осн. задач исследования гальваномагнитных явлений в полупроводниках. Эффективные массы
носителей в полупроводниках  ,
как правило, меньше массы свободного электрона m0 (в металле
~m0), благодаря чему значение H0 и Нкв
для полупроводников меньше, чем для металлов. Для ряда полупроводников Н0~(0,1-1)*104Э,
а условие Н>НКВ может быть достигнуто при T~10K. На гальваномагнитных явлениях в полупроводниках существ. влияние оказывает наличие неск. сортов
носителей. Вклад разл. групп носителей в магнетосопротивление не аддитивен (в
отличие от вклада в электропроводность). У полупроводников, имеющих один сорт
носителей (для определённости - электронов
с изотропным квадратичным законом дисперсии), при
,
как правило, меньше массы свободного электрона m0 (в металле
~m0), благодаря чему значение H0 и Нкв
для полупроводников меньше, чем для металлов. Для ряда полупроводников Н0~(0,1-1)*104Э,
а условие Н>НКВ может быть достигнуто при T~10K. На гальваномагнитных явлениях в полупроводниках существ. влияние оказывает наличие неск. сортов
носителей. Вклад разл. групп носителей в магнетосопротивление не аддитивен (в
отличие от вклада в электропроводность). У полупроводников, имеющих один сорт
носителей (для определённости - электронов
с изотропным квадратичным законом дисперсии), при 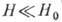 постоянная Холла равна:
постоянная Холла равна:

где 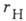 - холл-фактор, величина к-рого определяется зависимостью времени t релаксации
носителей от энергии
- холл-фактор, величина к-рого определяется зависимостью времени t релаксации
носителей от энергии 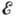 (табл.).
Для характеристики эффекта Холла часто используют т. н. холловскую подвижность
(табл.).
Для характеристики эффекта Холла часто используют т. н. холловскую подвижность
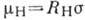 , где
, где 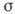 -
электропроводность при H=0. С дрейфовой подвижностью
-
электропроводность при H=0. С дрейфовой подвижностью 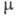 она связана соотношением
она связана соотношением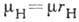 (на опыте обычно измеряется именно
(на опыте обычно измеряется именно 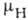 ,
а по ней судят о величине
,
а по ней судят о величине 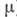 ).
Поперечное магнетосопротивление определяется выражением (
).
Поперечное магнетосопротивление определяется выражением (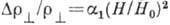 ,
где
,
где 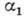 зависит от
механизма рассеяния (табл.).
зависит от
механизма рассеяния (табл.).
При 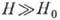 , как и в металлах,
, как и в металлах, 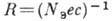 и не зависит от механизма рассеяния. Это обстоятельство используется для определения
концентрации носителей
и не зависит от механизма рассеяния. Это обстоятельство используется для определения
концентрации носителей 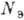 .
Для поперечного магнетосопротивления теория предсказывает насыщение:
.
Для поперечного магнетосопротивления теория предсказывает насыщение: 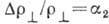 ,
где
,
где 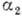 не зависит
от H (табл.). Однако на опыте насыщения часто не наблюдается. Причины
этого - в искривлении линий тока в магн. поле; искривление обусловлено наличием
в образце неоднородностей, а также конечными размерами образца. Наиб. ярко явление
выражено в полупроводниках с большой подвижностью носителей. Магнетосопротивление
очень чувствительно к анизотропии энергетич. спектра носителей. Так
не зависит
от H (табл.). Однако на опыте насыщения часто не наблюдается. Причины
этого - в искривлении линий тока в магн. поле; искривление обусловлено наличием
в образце неоднородностей, а также конечными размерами образца. Наиб. ярко явление
выражено в полупроводниках с большой подвижностью носителей. Магнетосопротивление
очень чувствительно к анизотропии энергетич. спектра носителей. Так 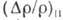 (отсутствующее в случае изотропного спектра) определяется гофрировкой изоэнергетич.
поверхностей в импульсном пространстве (напр., в p-Ge и р-Si).
(отсутствующее в случае изотропного спектра) определяется гофрировкой изоэнергетич.
поверхностей в импульсном пространстве (напр., в p-Ge и р-Si).
Если полупроводник имеет
и электроны и дырки с подвижностями 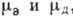 , то при
, то при 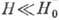 , согласно
(7) и (8):
, согласно
(7) и (8):
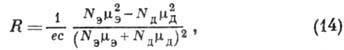
откуда R =0 при
(NЭ/NД) -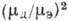 , а не при N3 =NД ( mД/mЭ,
как правило, мало).
, а не при N3 =NД ( mД/mЭ,
как правило, мало).
При  величина R зависит от соотношения между (Н/Н0)2
и
величина R зависит от соотношения между (Н/Н0)2
и 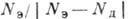 . Если
. Если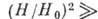
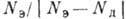 ,
то
,
то 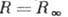 [см. (12)].
Если
[см. (12)].
Если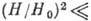
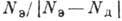 ,
то
,
то
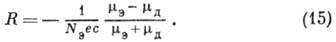
Измерения температурных
зависимостей постоянной Холла и магнетосопротивления при 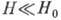 и
и 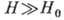 дают информацию
об отношении концентраций носителей и их подвижностей при разл. температурах.
дают информацию
об отношении концентраций носителей и их подвижностей при разл. температурах.
В Ge, Si и InSb р-типа
есть 2 сорта дырок, и следует учесть, что в области собств. проводимости имеется
3 типа носителей, а в области примесной проводимости - 2. В последнем случае
осн. вклад в электропроводность при H=0 дают тяжёлые дырки, несмотря
на то, что их 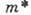 больше. Времена релаксации обеих групп
дырок практически равны; отношение их концентраций пропорционально отношению
плотностей состояний, т. е.
больше. Времена релаксации обеих групп
дырок практически равны; отношение их концентраций пропорционально отношению
плотностей состояний, т. е. 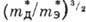 , а отношение подвижностей -
, а отношение подвижностей - 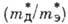 .
В итоге отношение вкладов в электропроводность порядка
.
В итоге отношение вкладов в электропроводность порядка 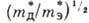 .
Вклад же в R при
.
Вклад же в R при 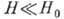 определяется отношением
определяется отношением 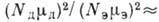
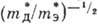 . T. о., постоянную Холла в слабых полях определяют лёгкие дырки, несмотря на
то, что концентрация их меньше.
. T. о., постоянную Холла в слабых полях определяют лёгкие дырки, несмотря на
то, что концентрация их меньше.
В полупроводниках относительно
слабые электрич. поля вызывают неравномерность распределения носителей по энергиям
- возникают "горячие" носители заряда, наблюдается нарушение закона
Ома (1). Сила Лоренца отклоняет носители от направления дрейфа в электрич. поле.
В итоге передача энергии от электрич. поля носителям уменьшается - магн. поле
"охлаждает" носители. Соответственно возникают дополнит. изменения
кинетич. коэффициентов. Наиб. ярко это проявляется в многодолинных полупроводниках, где под действием электрич. поля E существенно изменяются
заселённости долин. Поэтому и R и 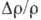 в многодолинных полупроводниках существенно зависят от Е. Магн.
поле изменяет неравновесную заселённость долин. В итоге оказывается, что в электрич.
поле возникает нечётная по H часть магнетосопротивления. Эта часть
в многодолинных полупроводниках существенно зависят от Е. Магн.
поле изменяет неравновесную заселённость долин. В итоге оказывается, что в электрич.
поле возникает нечётная по H часть магнетосопротивления. Эта часть
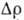 в достаточно
сильном электрич. поле может быть больше чётной, так что при соответствующих
направлениях H
в достаточно
сильном электрич. поле может быть больше чётной, так что при соответствующих
направлениях H 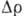 становится
отрицательным (наблюдалось в n-Ge и n-Si). Изучение гальваномагнитных явлений в такой
ситуации - метод исследования характеристик горячих носителей (см. Горячие
электроны).
становится
отрицательным (наблюдалось в n-Ge и n-Si). Изучение гальваномагнитных явлений в такой
ситуации - метод исследования характеристик горячих носителей (см. Горячие
электроны).
В квантующих магн. полях
в вырожденных полупроводниках, как и в металлах, возникают осцилляции продольного
и поперечного магнетосопротивления. Амплитуда осцилляционных пиков зависит от
температуры носителей; измерения этих величин использовались для изучения зависимости
температуры электронов от приложенного электрич. поля, причём по кинетике этого
процесса удаётся оценить время релаксации энергии электронов. В сильных магн.
полях, когда заполнено мало уровней, осцилляции выражены гораздо ярче, чем в
типичных металлах. В случае невырожденных носителей зависимости 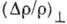 и
и 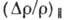 от H
и T характеризуются степенными функциями, причём показатели степени зависят
от механизма рассеяния (табл.). Постоянная Холла при
от H
и T характеризуются степенными функциями, причём показатели степени зависят
от механизма рассеяния (табл.). Постоянная Холла при 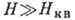 не зависит от механизма рассеяния и определяется тем же выражением, что и в
классич. области.
не зависит от механизма рассеяния и определяется тем же выражением, что и в
классич. области.
Осцилляции поперечного
и продольного магнето-сопротивления, а также постоянной Холла (со значительно
меньшей амплитудой при не слишком низкой температуре) наблюдаются в нек-рых полупроводниках
(GaSb, HgTe) за счёт магнитофононного резонанса и его аналогов.
Сильное магн. поле влияет
не только на энергетич. спектр электронов в зоне проводимости, но и на примесные
состояния: волновая функция примесного состояния "сжимается" в плоскости,
перпендикулярной H. В результате энергия ионизации примесного
атома возрастает, что, в свою очередь, приводит к уменьшению концентрации носителей
в зоне проводимости (мат. "вымораживание" носителей). В большинстве
случаев, однако, волновые функции примесных атомов перекрываются с образованием
примесной зоны. В такой ситуации осн. роль в электропроводности играют "прыжки"
носителей по примесям без активации в зону проводимости (прыжковая проводимость). Деформация волновых функций примесей в магн. поле, приводящая к уменьшению
их перекрытия, существенно влияет на электросопротивление. Характерной особенностью
прыжкового механизма является гигантское положит. магнетосопротивление, зависящее
от H по закону expF(H). Вид функции F(H)определяется соотношением
между H и нек-рым характерным значением 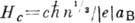 , где аВ- эфф. боровский радиус примесного состояния. При
, где аВ- эфф. боровский радиус примесного состояния. При
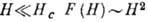 ; при
; при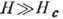
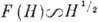 Экспоненциальная зависимость магнетосопротивления от H измерялась экспериментально
(в n=InAs сопротивление увеличивалось в 105 раз при изменении
Н от 2,8*104 до 14*104 T). Наблюдение гигантского
магнетосопротивления - один из способов идентификации механизма прыжковой проводимости в полупроводниках.
Экспоненциальная зависимость магнетосопротивления от H измерялась экспериментально
(в n=InAs сопротивление увеличивалось в 105 раз при изменении
Н от 2,8*104 до 14*104 T). Наблюдение гигантского
магнетосопротивления - один из способов идентификации механизма прыжковой проводимости в полупроводниках.

|
|