Динамика кристаллической решётки - раздел физики твёрдого тела, посвящённый изучению движений атомов в кристалле
с учётом дискретности его структуры. Включает классич. и квантовую механику
коллективных движений атомов в идеальном кристалле, динамику дефектов кристаллич. решётки, теорию взаимодействия кристалла с проникающим излучением,
описание физ. механизмов пластичности и прочности кристаллич. тел.
Колебания идеального
кристалла. Частицы, составляющие кристалл (атомы, ионы или молекулы), под
действием внеш. сил
или в результате теплового движения могут смещаться относительно своих положений
равновесия - узлов кристаллич. решётки. Наличие межатомного взаимодействия делает
невозможными независимые смещения отд. атомов, и их коллективное движение приобретает
характер колебат. процесса, распространяющегося в виде волн по кристаллу. Если
смещения атомов малы, то силы межатомного взаимодействия оказываются пропорциональными
смещениям и моделью колеблющегося кристалла может служить система частиц, связанных
упругими пружинками. Предположение об упругом характере сил, удерживающих атомы
в положении равновесия, наз. гармоническим приближением. Оно приводит к ур-ниям
колебаний вида:
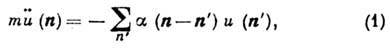
где n - радиус-вектор
узла кристаллич. решётки, занятого атомом в равновесии, 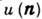 - смещение атома из n-го узла, то - масса атома,
- смещение атома из n-го узла, то - масса атома, 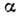 - матрица упругих коэффициентов (динамическая матрица кристалла, см. Модули
упругости). Предполагается, что
- матрица упругих коэффициентов (динамическая матрица кристалла, см. Модули
упругости). Предполагается, что 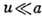 ,
где а - межатомное расстояние (период решётки).
,
где а - межатомное расстояние (период решётки).
Собственными функциями ур-ния
(1) являются нормальные колебания (моды) типа:
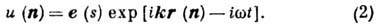
Здесь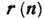 - координата
- координата 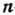 -го
кристаллич. узла,
-го
кристаллич. узла, 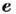 -
вектор поляризации, определяющий направление индивидуального движения атома,
-
вектор поляризации, определяющий направление индивидуального движения атома, -
квазиволновой вектор (
-
квазиволновой вектор (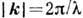 ,
где
,
где  - длина волны
колебания),
- длина волны
колебания),  -
частота. В процессе нормальных колебаний все атомы кристалла колеблются около
своих положений равновесия по гармонич. закону с одинаковой частотой
-
частота. В процессе нормальных колебаний все атомы кристалла колеблются около
своих положений равновесия по гармонич. закону с одинаковой частотой 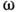 .
Независимые колебания отличаются разл. векторами
.
Независимые колебания отличаются разл. векторами 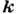 ,
лежащими внутри первой Бриллюэна зоны, а также целочисленным параметром,
определяющим ветвь закона дисперсии, связывающего величины
,
лежащими внутри первой Бриллюэна зоны, а также целочисленным параметром,
определяющим ветвь закона дисперсии, связывающего величины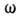 и
и  :
:
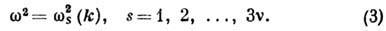
Здесь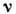 -
число атомов в элементарной ячейке кристалла. Закон дисперсии (3) описывается
периодич. функцией вектора
-
число атомов в элементарной ячейке кристалла. Закон дисперсии (3) описывается
периодич. функцией вектора 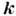 с периодами обратной решётки, равными по порядку величины
с периодами обратной решётки, равными по порядку величины 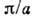 .
Число мод равно числу степеней свободы всех частиц кристалла. В гармонич. приближении
любое движение атомов кристалла может быть представлено в виде суперпозиции
нормальных колебаний.
.
Число мод равно числу степеней свободы всех частиц кристалла. В гармонич. приближении
любое движение атомов кристалла может быть представлено в виде суперпозиции
нормальных колебаний.
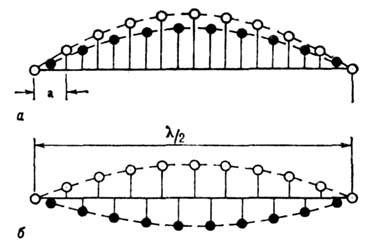
Рис. 1. Схема длинноволновых
колебаний одномерного кристалла: а - акустические колебания; б - оптические
колебания (а - период решётки).
Всегда существуют три ветви
колебаний (т. н. акустические колебания), при к-рых в длинноволновом приближении
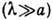 все атомы в элементарной
ячейке колеблются в одной фазе (рис. 1, а) и закон дисперсии к-рых линеен:
все атомы в элементарной
ячейке колеблются в одной фазе (рис. 1, а) и закон дисперсии к-рых линеен:
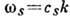 , s=1, 2, 3. При
, s=1, 2, 3. При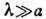 это обычные звуковые волны в твёрдом теле (с - фазовая
скорость их распространения) и описывающие их ур-ния (1) превращаются в динамич.
ур-ния теории упругости. Если
это обычные звуковые волны в твёрдом теле (с - фазовая
скорость их распространения) и описывающие их ур-ния (1) превращаются в динамич.
ур-ния теории упругости. Если  совпадает с высокосимметричным кристаллографич. направлением (см. Симметрия
кристаллов), акустич. колебания разделяются на одно продольное и два поперечных.
Акустич, колебания охватывают диапазон частот от 0 до
совпадает с высокосимметричным кристаллографич. направлением (см. Симметрия
кристаллов), акустич. колебания разделяются на одно продольное и два поперечных.
Акустич, колебания охватывают диапазон частот от 0 до  с-1. При более высоких частотах
с-1. При более высоких частотах 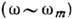 закон дисперсии акустич. колебаний отличается от звукового - он перестаёт быть
линейным (рис. 2).
закон дисперсии акустич. колебаний отличается от звукового - он перестаёт быть
линейным (рис. 2).
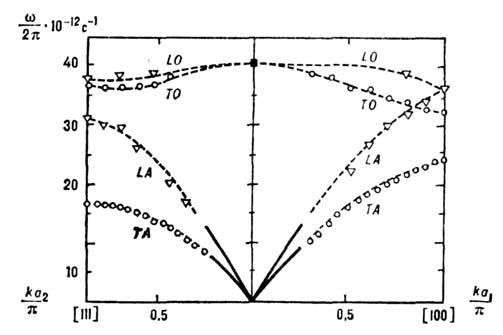
Рис. 2. Законы дисперсии
акустических (А) и оптических (О) колебаний с продольной (L)и поперечной
(Т) поляризацией для алмаза в двух кристаллографических направлениях, восстановленные
нейтроннографическим методом.
В простой кристаллич. решётке
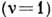 существуют только
акустич. колебания. В сложной кристаллич. решётке
существуют только
акустич. колебания. В сложной кристаллич. решётке 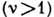 возможны также
возможны также 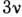 -3
ветвей колебаний (т. н. оптические колебания), характеризующиеся тем, что при
-3
ветвей колебаний (т. н. оптические колебания), характеризующиеся тем, что при
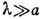 центр масс элементарной
ячейки покоится и происходят относительные смещения разных атомов внутри элементарной
ячейки (рис. 1, б).
центр масс элементарной
ячейки покоится и происходят относительные смещения разных атомов внутри элементарной
ячейки (рис. 1, б).
В ионных кристаллах, элементарная ячейка к-рых состоит из ионов противоположных знаков, оптич.
колебания сопровождаются колебаниями электрич. поляризации и потому связаны
с эл--магн. колебаниями в ИК-области частот. Название "оптич. колебания"
связано с резонансным поглощением эл--магн. излучения соответствующей частоты.
Частоты оптич. колебаний
лежат выше частот акустич. колебаний (рис. 2). Полосы частот акустич. и оптич.
колебаний могут перекрываться, но могут быть разделёнными запрещёнными зонами
частот.
Часто при качественном
описании колебаний кристаллич. решётки и при оценке их вклада в разл. физ. явления
(а иногда при теоретич. расчётах) используется теория Дебая. Эта теория основана
на предположении, что каждая акустич. ветвь колебаний имеет линейный закон дисперсии
при всех частотах в интервале 0-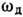 ,
где дебаевская частота
,
где дебаевская частота 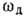 находится из условия равенства числа колебаний в каждой ветви числу атомов в
кристалле. Оказывается, что
находится из условия равенства числа колебаний в каждой ветви числу атомов в
кристалле. Оказывается, что 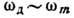 (см. Дебая теория твёрдого тела).
(см. Дебая теория твёрдого тела).
Важнейшей характеристикой
спектра колебаний кристалла является функция распределения частот 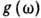 , определяющая спектральную плотность колебаний. функция
, определяющая спектральную плотность колебаний. функция 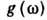 однозначно связана с законом дисперсии. При низких частотах
однозначно связана с законом дисперсии. При низких частотах 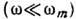 она не отличается от плотности акустич. колебаний и совпадает с ней:
она не отличается от плотности акустич. колебаний и совпадает с ней: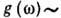
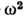 .
В интервале
.
В интервале 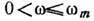 функция
функция
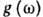 обладает син-гулярностями:
при нек-рых частотах её производная обращается в бесконечность (см. Ван Хова
особенности). Такая особенность, в частности, имеется на краю спектра частот
при
обладает син-гулярностями:
при нек-рых частотах её производная обращается в бесконечность (см. Ван Хова
особенности). Такая особенность, в частности, имеется на краю спектра частот
при 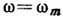 , где
, где  (рис. 3). Плотность колебаний чувствительна к наличию дефектов в кристалле.
Знание функции
(рис. 3). Плотность колебаний чувствительна к наличию дефектов в кристалле.
Знание функции 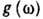 необходимо при расчёте
термодинамич. характеристик кристалла, она определяет температурную зависимость
тепловых характеристик кристалла (теплоёмкости, теплопроводности и др.) при
низких температурах.
необходимо при расчёте
термодинамич. характеристик кристалла, она определяет температурную зависимость
тепловых характеристик кристалла (теплоёмкости, теплопроводности и др.) при
низких температурах.
Интенсивность тепловых
колебаний термодинамически равновесного кристалла зависит от отношения его температуры
T к Дебая температуре 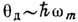 . При высоких темп-pax
. При высоких темп-pax 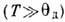 ср. квадрат смещения любого атома
ср. квадрат смещения любого атома 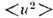 пропорционален T. В соответствии с неопределенностей соотношением при T=0 К,
пропорционален T. В соответствии с неопределенностей соотношением при T=0 К,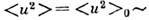
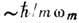 . Отличная от нуля величина
. Отличная от нуля величина  связана с квантовым характером движения атомов и определяет квадрат амплитуды
т. н. нулевых колебаний. Условием устойчивости кристаллич. состояния является
требование
связана с квантовым характером движения атомов и определяет квадрат амплитуды
т. н. нулевых колебаний. Условием устойчивости кристаллич. состояния является
требование 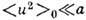 . Это
требование не выполняется в т. н. квантовых кристаллах, динамика к-рых
обладает рядом особенностей. Напр., в гелии нулевые колебания столь велики,
что он остаётся жидким вплоть до абс. нуля и затвердевает только под давлением.
. Это
требование не выполняется в т. н. квантовых кристаллах, динамика к-рых
обладает рядом особенностей. Напр., в гелии нулевые колебания столь велики,
что он остаётся жидким вплоть до абс. нуля и затвердевает только под давлением.
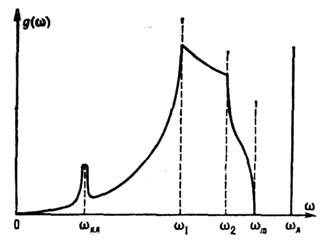
Рис. 3. Схематический вид
графика 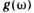 для одной
ветви акустических колебаний;
для одной
ветви акустических колебаний;  - положения особенностей ван Хова,
- положения особенностей ван Хова, 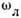 -
локальная частота,
-
локальная частота, 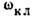 - квазилокальная частота.
- квазилокальная частота.
При квантовом описании
малых колебаний кристалла каждому нормальному колебанию с вектором k
можно сопоставить квазичастицу с квазиимпульсом 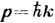 и энергией
и энергией 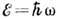 (см.
Корпускулярно-волновой дуализм ).Эти квазичастицы наз. фононами и
являются элементарными возбуждениями (квантами) поля упругих колебаний кристалла.
Слабо возбуждённое состояние кристалла в термодинамич. отношении эквивалентно
разреженному бозе-газу фононов, что позволяет для описания тепловых и
электрич. свойств кристалла использовать методы статистич. механики идеального
бозе-газа. В частности, решёточная теплоёмкость кристалла вычисляется
как теплоёмкость газа фононов. Теплопроводность диэлектрич. кристалла
определяется кинетикой фононов, рассеивающихся друг на друге и на дефектах кристаллич.
решётки. В металлах рассеяние электронов на фононах даёт основной вклад в электросопротивление.
(см.
Корпускулярно-волновой дуализм ).Эти квазичастицы наз. фононами и
являются элементарными возбуждениями (квантами) поля упругих колебаний кристалла.
Слабо возбуждённое состояние кристалла в термодинамич. отношении эквивалентно
разреженному бозе-газу фононов, что позволяет для описания тепловых и
электрич. свойств кристалла использовать методы статистич. механики идеального
бозе-газа. В частности, решёточная теплоёмкость кристалла вычисляется
как теплоёмкость газа фононов. Теплопроводность диэлектрич. кристалла
определяется кинетикой фононов, рассеивающихся друг на друге и на дефектах кристаллич.
решётки. В металлах рассеяние электронов на фононах даёт основной вклад в электросопротивление.
Нелинейные эффекты.
В действительности колебания кристалла не являются строго гармоническими. Несмотря
на малость энгармонизма, при слабых возбуждениях нормальные колебания кристалла
оказываются связанными друг с другом (фононы образуют неидеальный газ, т. е.
взаимодействуют между собой), а закон дисперсии оказывается зависящим от температуры.
Наличие энгармонизма (взаимодействие между фононами), в частности, объясняет
тепловое расширение кристалла.
При сильном возбуждении
смещения атомов не малы, и описывающие их ур-ния становятся нелинейными. В таких
условиях возможны движения, существенно отличающиеся от гармонич. колебаний.
Импульсная макроскопич. нагрузка вызывает в кристалле ударную волну. Импульсный
нагрев может создать тепловой солитон - особый тип коллективного локализованного
возбуждения, способного перемещаться с большой скоростью по кристаллу. Если
же интенсивное внеш. воздействие сосредоточено на одном атоме (напр., удар быстрой
частицы по поверхности кристалла), то сообщённый крайнему атому импульс может
передаваться на большие расстояния вдоль плотно упакованного атомного
ряда, в чём проявляется фокусирующее действие кристаллич. решётки (см. Теней
эффект, Каналирование заряженных частиц).
Динамич. нелинейность кристалла
проявляется при структурных фазовых переходах (напр., в сегнетоэлектриках). Частота нек-рого оптич. фонона зависит от температуры и при температуре фазового
превращения обращается в нуль, приводя к перестройке элементарной ячейки кристалла.
Колебания кристалла
с дефектами. На Д. к. р. существенно влияют дефекты решётки, изменяющие
в ур-нии (1) массу m частицы (дефекты-примеси) и элементы матрицы 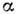 (точечные и протяжённые дефекты). Нормальные колебания реального кристалла с
дефектами уже не являются плоскими волнами, как (2). Среди нормальных мод могут
появиться колебания, полностью локализованные вблизи дефекта (локальные колебания).
Им отвечают частоты, лежащие выше предельной частоты идеального кристалла или
попадающие в запрещённые зоны (рис. 3). Если имеется много однотипных точечных
дефектов, то локальное колебание на одном дефекте может "перескочить"
на другой (как при резонансе слабо связанных маятников). В таком случае дефектный
кристалл обладает примесной зоной частот колебаний.
(точечные и протяжённые дефекты). Нормальные колебания реального кристалла с
дефектами уже не являются плоскими волнами, как (2). Среди нормальных мод могут
появиться колебания, полностью локализованные вблизи дефекта (локальные колебания).
Им отвечают частоты, лежащие выше предельной частоты идеального кристалла или
попадающие в запрещённые зоны (рис. 3). Если имеется много однотипных точечных
дефектов, то локальное колебание на одном дефекте может "перескочить"
на другой (как при резонансе слабо связанных маятников). В таком случае дефектный
кристалл обладает примесной зоной частот колебаний.
Локальные колебания протяжённых
дефектов (напр., дислокации или дефекта упаковки) распространяются вдоль
них в виде волн, не проникающих в объём кристалла и отличающихся законом дисперсии
от объёмных волн. Таковы колебания у свободной поверхности твёрдого тела (Рзлея
волны).
Наряду с локальными колебаниями
могут существовать т. н. квазилокальные колебания, к-рые охватывают весь кристалл,
но при к-рых амплитуда колебаний дефекта значительно превосходит амплитуду колебаний
атомов в объёме. Частоты таких колебаний попадают в полосы частот идеального
кристалла и обычно оказываются расположенными вблизи краёв этих полос. Плотность
колебаний имеет узкий резонансный пик на квазилокальной частоте (рис. 3).
Как локальные, так и квазилокальные
колебания проявляются в возникновении дополнит. линий в спектрах поглощения
ИК-излучения (см. Инфракрасная спектроскопия ),в особенностях упругого
рассеяния нейтронов (см. Нейтронография)и мёссбауэровских спектров (см.
Мёссбауэровская спектроскопия).
Динамика дефектов.
Точечные дефекты типа примесей, вакансий или междоузельных атомов способны
перемещаться в кристалле путём диффузии. Но классич. диффузию нельзя
считать динамич. процессом, т. к. очередной скачок дефекта имеет случайное направление
и только усреднение по большому числу дефектов может дать нек-рую направленность
их движению. Иначе могут вести себя точечные дефекты в квантовом кристалле,
когда для дефекта появляется возможность перехода из одного положения в соседнее
путём квантового туннелирования (см. Туннельный эффект ).В результате
дефект может превратиться в квазичастицу - дефектон ,свободно перемещающуюся
в кристалле.
Междоузельный атом приобретает
способность к механич. перемещению в т. н. краудионной конфигурации даже в классич.
кристалле (см. Краудион). "Лишний" атом оказывается
как бы распределённым между неск. узлами плотно упакованного атомного ряда и
потому легко перемещается вдоль этого направления.
Чисто механич, перемещение
(скольжение) характерно для специфического линейного дефекта - дислокации. Смещение
её линии по плоскости скольжения не нарушает сплошности кристалла, а потому
происходит сравнительно легко. Движение дислокации всегда связано с неупругим
изменением формы кристаллич. образца, поэтому дислокация является элементарным
носителем пластичности кристалла. Атомная перестройка, сопровождающая
перемещение дислокации, требует не очень больших нагрузок, и в этом причина
того, что пластич.
деформация кристалла начинается при напряжениях, малых по сравнению с теоретич.
прочностью кристалла.
Нестационарное движение
дислокации (с ускорением) сопровождается изучением упругих (звуковых) волн,
подобно тому как нестационарное движение электрич. зарядов приводит к излучению
эл--магн. волн. С др. стороны, взаимодействуя с интенсивными колебаниями кристалла,
дислокация вовлекается в осцилляторное диссипативное движение и даёт важный
вклад во внутреннее трение.
Двухмерные дефекты типа
двойников (см. Двойникование), трещин или мартенситных включений
также могут проявлять себя как динамич. образования. Наряду с дислокациями они
играют определяющую роль в пластичности и прочности кристаллов.
Взаимодействие с проникающим
излучением. Динамич. взаимодействие кристалла с фотонами разной энергии
(в т. ч. рентгеновскими и 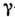 -квантами),
нейтронами или ускоренными заряж. частицами имеет разное проявление в зависимости
от энергии и импульса, передаваемых кристаллу дроникающей частицей. Если эта
энергия сравнима с
-квантами),
нейтронами или ускоренными заряж. частицами имеет разное проявление в зависимости
от энергии и импульса, передаваемых кристаллу дроникающей частицей. Если эта
энергия сравнима с 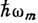 , а передаваемый импульс имеет порядок величины
, а передаваемый импульс имеет порядок величины 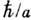 ,
то происходит неупругий процесс рассеяния частицы, сопровождающийся рождением
одного или неск. фононов. Изучение таких процессов позволяет определить закон
дисперсии колеблющегося кристалла (рис. 2). Однако возможен процесс без отдачи,
при к-ром энергия частицы сохраняется и в кристалле не происходит рождения фонона.
Такие процессы (типа Мёссбауэра эффекта)характеризуются предельно узкими
дифракционными линиями, и их доля измеряется Дебая - Уоллера фактором.
,
то происходит неупругий процесс рассеяния частицы, сопровождающийся рождением
одного или неск. фононов. Изучение таких процессов позволяет определить закон
дисперсии колеблющегося кристалла (рис. 2). Однако возможен процесс без отдачи,
при к-ром энергия частицы сохраняется и в кристалле не происходит рождения фонона.
Такие процессы (типа Мёссбауэра эффекта)характеризуются предельно узкими
дифракционными линиями, и их доля измеряется Дебая - Уоллера фактором.
Если кинетич. энергия частицы
велика, то она способна выбить атомы кристалла из равновесных положений, сообщая
им значит. энергию и превращая их в движущиеся дефекты. Они, в свою очередь,
создают вторичные смещения атомов и смещения более высоких порядков, в результате
чего возникает каскад точечных дефектов. Однако существуют такие направления,
параллельные атомным рядам и атомным плоскостям ("каналы"), вдоль
к-рых быстрые заряж. частицы с длиной волны де Бройля, значительно меньшей а,
движутся, практически не вызывая смещения атомов. Явление каналирования частиц
различно для частиц разного знака зарядов (электронов и позитронов и т. п.).

A. M. Косевич
Релятивисты и позитивисты утверждают, что "мысленный эксперимент" весьма полезный интрумент для проверки теорий (также возникающих в нашем уме) на непротиворечивость. В этом они обманывают людей, так как любая проверка может осуществляться только независимым от объекта проверки источником. Сам заявитель гипотезы не может быть проверкой своего же заявления, так как причина самого этого заявления есть отсутствие видимых для заявителя противоречий в заявлении.
Это мы видим на примере СТО и ОТО, превратившихся в своеобразный вид религии, управляющей наукой и общественным мнением. Никакое количество фактов, противоречащих им, не может преодолеть формулу Эйнштейна: "Если факт не соответствует теории - измените факт" (В другом варианте " - Факт не соответствует теории? - Тем хуже для факта").
Максимально, на что может претендовать "мысленный эксперимент" - это только на внутреннюю непротиворечивость гипотезы в рамках собственной, часто отнюдь не истинной логики заявителя. Соответсвие практике это не проверяет. Настоящая проверка может состояться только в действительном физическом эксперименте.
Эксперимент на то и эксперимент, что он есть не изощрение мысли, а проверка мысли. Непротиворечивая внутри себя мысль не может сама себя проверить. Это доказано Куртом Гёделем.
Понятие "мысленный эксперимент" придумано специально спекулянтами - релятивистами для шулерской подмены реальной проверки мысли на практике (эксперимента) своим "честным словом". Подробнее читайте в FAQ по эфирной физике.
|
|