Бозе-газ - газ из частиц, подчиняющихся квантовой Бозе статистике. Бозе-газы являются,
напр., 4He, атомы к-рого содержат чётное число нуклонов, и газы фотонов
(квантов эл--магн. поля) и нек-рых квазичастиц, напр. фононов (элементарных
возбуждений кристаллич. решётки).
Если можно пренебречь взаимодействием
между частицами, Бозе-газ наз. идеальным. В идеальном Бозе-газе при темп-pax ниже вырождения
температуры наступает Бозе - Эйнштейна конденсация, при к-рой макроскопически
большое число частиц обладает нулевым импульсом (образует бозе-конденсат).
Для вырожденного слабонеидеального Бозе-газа малые возбуждения вблизи осн. состояния ведут себя как газ квазичастиц,
подчиняющихся статистике Бозе, т. е. гамильтониан
Бозе-газ можно приближённо представить в виде:
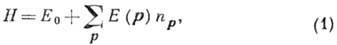
где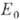 
-
энергия осн. состояния, 
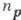- числа заполнения для квазичастиц с импульсом 
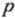и массой т, принимающие значения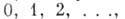
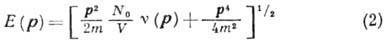
- энергия квазичастиц,
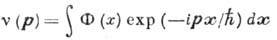
- фурье-компонента
потенциала взаимодействия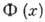 
, 
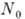- число частиц
в конденсате, V - объём; для слабонеидеального Бозе-газа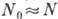 
,
где N - число частиц. При малых импульсах р спектр в (2) имеет
фононный характер, т. е. 
,
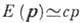где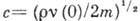 
- скорость звука
в Бозе-газе,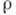 
-
плотность газа. При больших импульсах ф-ла (2) переходит в спектр идеального
газа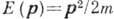 
. Осн. член
под знаком корня в ф-ле (2) пропорционален потенциалу взаимодействия, следовательно
этот результат нельзя получить с помощью простой теории возмущений, основанной
на разложении по степеням потенциала взаимодействия. Эта трудность была разрешена
H. H. Боголюбовым в 1947.
Метод Боголюбова основан
на том, что при нулевой температуре в неидеальном Бозе-газе со слабым взаимодействием
большая часть частиц N0 находится в "конденсате"
с нулевым импульсом, поэтому бозе-операторы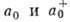 
уничтожения и рождения частиц с нулевым импульсом (к-рые удовлетворяют перестановочному
соотношению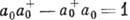 
) можно считать не операторами, а числами. Гамильтониан неидеального Бозе-газа в
представлении вторичного квантования имеет вид:
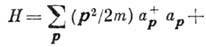
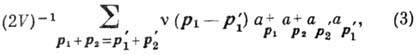
где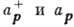 
- операторы рождения и уничтожения бозе-частиц
с импульсом р, удовлетворяющие перестановочным соотношениям
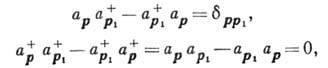
где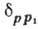 
-символ
Кронекера. Операторы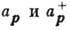 
можно рассматривать как малые величины по сравнению с 
,
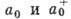ограничиться в гамильтониане квадратичными членами по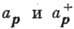 
и ввести вместо них новые
бозе-операторы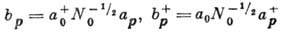
. Тогда гамильтониан принимает вид:
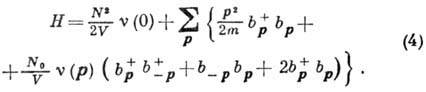
Этот гамильтониан представляет
собой квадратичную форму относительно операторов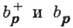 
и приводится к диагональному виду с помощью Боголюбова канонического преобразования. T. о., для энергии квазичастиц получается ф-ла (2). Анализ этой ф-лы показывает,
что модель слабонеидеального Бозе-газа может объяснить свойство сверхтекучести, типичное для квантовых жидкостей, а также образование вихревых нитей.
Удобно ввести эффективный
потенциал взаимодействия с той же длиной рассеяния а, но допускающий
применение теории возмущений. Тогда в борновском приближении заменяют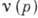 
величиной 
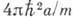. Условием
слабой неидеальности Бозе-газа служит неравенство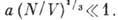 
Спектр Бозе-газа малой плотности
можно получить также методом Грина функций и методом коллективных
переменных . Спектр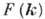 
квазичастиц Бозе-газа в общем случае можно выразить через структурный фактор 
:
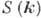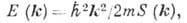
где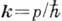 
- волновой вектор,
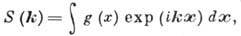
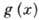- корреляц. функция плотности. Величину
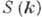можно получить из экспериментов по рассеянию нейтронов.
Д. H. Зубарев
|
|
 |
