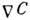 и имеет противоположное ему направление:
и имеет противоположное ему направление:Диффузия (от лат. diffusio - распространение, растекание, рассеивание) - неравновесный процесс,
вызываемый молекулярным тепловым движением и приводящий к установлению равновесного
распределения концентраций внутри фаз. В результате Д. происходит выравнивание
хим. потенциалов компонентов смеси. В однофазной системе при пост. температуре и
отсутствии внеш. сил Д. выравнивает концентрацию каждого компонента фазы по
объёму всей системы. Если темп-pa не постоянна или на систему действуют внеш.
силы, то в результате Д. устанавливается пространственно неоднородное равновесное
распределение концентраций каждого из компонентов (см. Термодиффузия, Электродиффузия).
Д.- частный случай переноса
явлений, относится к явлениям массопереноса. Она является одним из наиб.
общих кинетич. процессов, присущих газам, жидкостям и твёрдым телам, протекающих
в иих с разл. скоростью. Диффундировать могут также взвешенные малые частицы
посторонних веществ (вследствие броуновского движения), а также
собств. частицы вещества (самодиффузия ).Диффузия - необратимый процесс,
один из источников диссипации энергии в системе.
Скорость Д. (диффузионный
поток) в бинарной смеси при малой концентрации диффундирующего вещества пропорциональна
градиенту концентрации 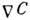 и имеет противоположное ему направление:
и имеет противоположное ему направление:
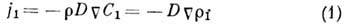
(j1 - диффузионный
поток, т. е. поток массы 1-го компонента через единичную площадку в единицу
времени, D - коэф. Д., 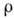 - полная плотность бинарной смеси,
- полная плотность бинарной смеси, 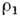 -
парциальная плотность 1-го компонента). Выражение (1) наз. 1-м законом Фика
[открыт А. Фиком (A. Fick) в 1855].
-
парциальная плотность 1-го компонента). Выражение (1) наз. 1-м законом Фика
[открыт А. Фиком (A. Fick) в 1855].
В табл. приведены для сравнения
коэфф. Д. в бинарной смеси для газов, жидкостей и твёрдых тел при атм. давлении:
|
Диффундирующее
вещество |
Основной компонент |
Температура, 0C |
D, м Vc |
||
|
Водород (газ) |
Кислород (газ) |
0 |
0,70*10-4 |
||
|
Пары воды |
Воздух |
0 |
0,23*10-4 |
||
|
Поваренная соль |
Вода |
20 |
1,1*10-9 |
||
|
Золото (твёрдое) |
Свинец (твёрдый) |
20 |
4*10-14 |
||
|
Свинец (твёрдый) |
Свинец (твёрдый) |
285 |
7*10-15 |
||
Диффузионный поток первого
компонента бинарной смеси при наличии градиента теми-ры 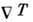 и градиента давления
и градиента давления 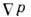 определяется ф-лой
определяется ф-лой
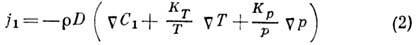
где KТ
- коэф. термодиффузии,
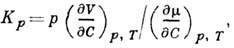
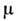 - разность хим. потенциалов
- разность хим. потенциалов 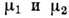 компонентов; величина КpD паз. коэф. бародиффузии.
компонентов; величина КpD паз. коэф. бародиффузии.
При стремлении концентрации
к нулю коэф. Д. стремится к конечной постоянной. Из условия сохранения массы
1-го компонента в случае малой концентрации следует диффузии уравнение

(2-й закон Фика). Матем.
теория ур-ния Д. совпадает с теорией теплопроводности уравнения.
Для смеси мн. компонентов
диффузионный поток каждого компонента ji, согласно термодинамике
необратимых процессов [1, 2], определяется градиентами хим. потенциалов 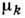 всех п компонентов смеси:
всех п компонентов смеси:
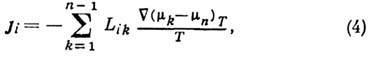
где Lik -
кинетич. коэф. Онсагера, имеющие тензорный характер и пропорциональные коэф.
Д. компонентов смеси (индекс означает, что рассматривается Д. i-гo компонента
относительно k-го). Градиенты хим. потенциалов берутся при фиксиров.
температуре T. Выражение (4) есть частный случай линейных соотношений Онсагера
между термодинамич. силами Д.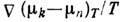 и диффузионными потоками. Согласно принципу Онсагера (см. Онсагера теорема), в отсутствие магн. поля симметрии
и диффузионными потоками. Согласно принципу Онсагера (см. Онсагера теорема), в отсутствие магн. поля симметрии 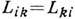 .
.
Среди градиентов хим. потенциалов
лишь n - 1 независимых, их можно выразить через градиенты концентраций
с помощью Гиббса - Дюгема уравнения и представить диффузионный поток
в виде

где Dik - тензор коэф. Д. Его диагональные элементы определяют прямые процессы Д.,
а недиагональные - перекрёстные диффузионные процессы. Соотношения
Онсагера для Dik имеют более сложный характер, чем для Lik [1, 2]. Для бинарной смеси коэф. D11 связан с коэф. Онсагера
L11 соотношением
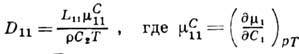
В процессе Д. происходит
возрастание энтропии, причём производство энтропии в единицу времени
равно:
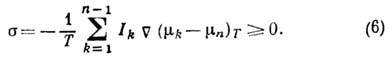
Если на смесь компонентов
действуют внеш. силы Fk (напр., гравитационные и инерциальные),
то явление Д. существенно меняется. Поскольку градиент давления 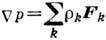 зависит от внеш. сил Fk, то термодинамич. силами являются
не только градиенты хим. потенциалов, но также и центробежная сила и сила тяготения
и возникает бародиффузия. При этом термодинамич. равновесию соответствует стационарное
неоднородное распределение концентраций. Процесс Д. стремится к установлению
этого распределения. Этот процесс позволяет определять молекулярные массы по
седиментации в центробежном поле в ультрацентрифуге.
зависит от внеш. сил Fk, то термодинамич. силами являются
не только градиенты хим. потенциалов, но также и центробежная сила и сила тяготения
и возникает бародиффузия. При этом термодинамич. равновесию соответствует стационарное
неоднородное распределение концентраций. Процесс Д. стремится к установлению
этого распределения. Этот процесс позволяет определять молекулярные массы по
седиментации в центробежном поле в ультрацентрифуге.
Броуновское движение взвешенных
частиц в жидкости можно рассматривать как Д. Cp. квадрат расстояния r, на
к-рое удалится броуновская частица за время t, пропорционально её коэф.
Д.: 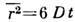 . Коэф. D взвешенных частиц определяется их подвижностью b (коэф. пропорциональности
между постоянной внеш. силой и скоростью), причём D = kTb (соотношение
Эйнштейна, установленное в 1905).
. Коэф. D взвешенных частиц определяется их подвижностью b (коэф. пропорциональности
между постоянной внеш. силой и скоростью), причём D = kTb (соотношение
Эйнштейна, установленное в 1905).
Диффузия в газах.
В газах Д. определяется ср. длиной свободного пробега  молекул, к-рая значительно больше ср. расстояния между ними. Коэфф. Д. для газа
молекул, к-рая значительно больше ср. расстояния между ними. Коэфф. Д. для газа
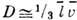 , где
, где 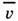 -
ср. скорость теплового движения частиц. Коэф. Д. обратно пропорционален давлению
газа (т. е.
-
ср. скорость теплового движения частиц. Коэф. Д. обратно пропорционален давлению
газа (т. е.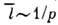 ) и
пропорционален
) и
пропорционален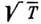 (т. к.
(т. к.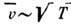 ). Более
детальные расчёты коэф. Д. в газах даёт решение кинетического уравнения Больцмана для неоднородного состояния газовой смеси при заданных градиентах концентраций
для спец. моделей межмолекулярных сил Чепмена - Энскога методом [3, 4].
). Более
детальные расчёты коэф. Д. в газах даёт решение кинетического уравнения Больцмана для неоднородного состояния газовой смеси при заданных градиентах концентраций
для спец. моделей межмолекулярных сил Чепмена - Энскога методом [3, 4].
В бинарной смеси газов,
молекулы к-рых взаимодействуют как твёрдые сферы с диаметрами 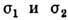 , коэф. Д. равен
, коэф. Д. равен
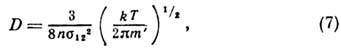
где 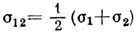 - ср. диаметр частиц; т' -- приведённая
масса:
- ср. диаметр частиц; т' -- приведённая
масса: 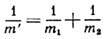 , где
m1 и m2 - массы частиц.
, где
m1 и m2 - массы частиц.
Для Д. лёгкого газа в тяжёлом
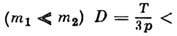 <v/
sтр> , где и -скорость лёгких атомов,
<v/
sтр> , где и -скорость лёгких атомов,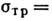
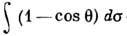 -транспортное сечение столкновения,
-транспортное сечение столкновения, 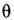 - угол между траекториями частиц,
- угол между траекториями частиц, 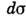 -дифференц.
эффективное сечение. Усреднение
-дифференц.
эффективное сечение. Усреднение 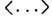 ведётся по распределению Максвелла лёгких частиц. Для диффузии тяжёлого газа
в лёгком
ведётся по распределению Максвелла лёгких частиц. Для диффузии тяжёлого газа
в лёгком
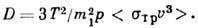
T. о., коэф. Д. связан
с транспортным эффективным сечением.
Для газа заряж. частиц,
напр. носителей заряда в полупроводниках, необходимо учитывать влияние объёмного
заряда и связанного с ним электрич. поля и свойства
квазинейтральности (см. Диффузия носителей заряда в полупроводниках).
Для диффузии частиц
в плазме существенно влияние электрич. и магн. полей. В плазме возможно
возникновение разл. неустойчивостей, меняющих процесс Д., существенно увеличивая
коэф. Д. Если магн. поле в плазме велико, коэф. Д. может быть очень малым (см.
Замагниченная плазма), что важно для осуществления УТC.
Диффузия в жидкостях.
Кинетич. теория Д. в жидкостях значительно сложнее, чем в газах, т. к. в жидкостях
ср. расстояние между молекулами того же порядка, что и радиус сил взаимодействия
между ними, и силы взаимодействия не столь малы, как в газах. Понятие свободного
пробега для жидкостей не имеет смысла, и для них не удаётся построить достаточно
обоснованного кинетич. ур-ния. Теория Д. в жидкостях (как и др. процессов переноса)
развивалась на двух разл. уровнях. Один из них основан на аналогии между структурой
жидкости и твёрдого тела [5-6], другой, более фундаментальный исходит из общих
принципов статистич. физики и представления о локальном равновесии [7].
В теориях первого типа
предполагается существование в жидкости ближнего порядка и процесс Д. определяется
скачками молекул из "оседлых" состояний в соседние вакантные состояния,
что связано с преодолением потенциального барьера. Каждый скачок происходит
при сообщении молекуле энергии, достаточной для разрыва её связей с соседними
молекулами и переходом в окружение др. молекул. Время "оседлой жизни"
во временном положении равновесия между активац. скачками 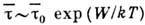 , где W - энергия активации,
, где W - энергия активации, 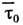 -
ср. период колебаний молекулы в "оседлом" состоянии
-
ср. период колебаний молекулы в "оседлом" состоянии  .
Коэф. Д. в жидкостях по порядку величины равен:
.
Коэф. Д. в жидкостях по порядку величины равен:
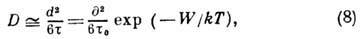
где d - ср. расстояние
между молекулами. С ростом температуры сильно уменьшается 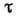 и несколько увеличивается d, поэтому D сильно возрастает. Экспоненциальная
зависимость D жидкости от температуры подтверждается экспериментально.
и несколько увеличивается d, поэтому D сильно возрастает. Экспоненциальная
зависимость D жидкости от температуры подтверждается экспериментально.
В более строгом варианте
элементарной теории Д. принимается, что структура жидкости отлична от структуры
твёрдых тел и размер вакансий изменяется (теория свободного объёма), так что
перескок возможен лишь начиная с нек-рого критич. размера вакансии.
Более фундам. теории Д.
в жидкостях основаны на том, что плотность числа молекул каждого из компонентов
ni(x)есть гидродинамич. переменная, медленно меняющаяся в
пространстве и во времени. Ей соответствует нек-рая макроскопич. плотность числа
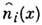 молекул i-й
компоненты, зависящей от координат её частиц и являющейся медленно меняющейся
динамич. переменной. Поэтому статистич. равновесие устанавливается в два этапа:
сначала в макроскопич. малых объёмах устанавливается локально равновесное распределение
молекул i-й
компоненты, зависящей от координат её частиц и являющейся медленно меняющейся
динамич. переменной. Поэтому статистич. равновесие устанавливается в два этапа:
сначала в макроскопич. малых объёмах устанавливается локально равновесное распределение
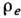 , подобное большому
каноническому распределению, соответствующему заданному неравновесному распределению
концентраций смеси, а затем оно медленно стремится к состоянию равновесия пропорционально
градиентам концентраций.
, подобное большому
каноническому распределению, соответствующему заданному неравновесному распределению
концентраций смеси, а затем оно медленно стремится к состоянию равновесия пропорционально
градиентам концентраций.
Локально равновесное распределение
имеет вид
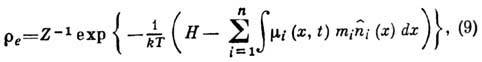
где Н-гамильтониан
системы, Z - нормировочная функция, зависящая от времени. Распределение 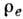 можно получить (в случае классич. статистич. механики), если
для каждого малого элемента объёма
можно получить (в случае классич. статистич. механики), если
для каждого малого элемента объёма 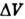 с числом частиц
с числом частиц 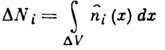 и
энергией DH=
и
энергией DH=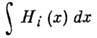 построить
большое канонич. распределение и перемножить эти распределения. Более строгий
метод получения
построить
большое канонич. распределение и перемножить эти распределения. Более строгий
метод получения 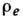 основан на экстремуме информац. энтропии (см. Энтропия в теории информации)
при заданных
основан на экстремуме информац. энтропии (см. Энтропия в теории информации)
при заданных  .
Распределение (9) при постоянных
.
Распределение (9) при постоянных 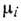 переходит в большое канонич. распределение Гиббса
переходит в большое канонич. распределение Гиббса
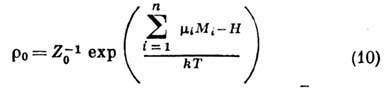
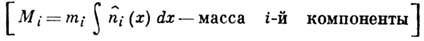 ,
,
к-рое удовлетворяет
Лиувилля уравнению. В случае малого отклонения системы от состояния статистич.
равновесия можно принять 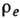 за 1-е приближение и найти к нему поправку, к-рая определяет неравновесный диффузионный
поток, пропорциональный термодинамич. силам
за 1-е приближение и найти к нему поправку, к-рая определяет неравновесный диффузионный
поток, пропорциональный термодинамич. силам 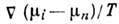 с коэф. Онсагера
с коэф. Онсагера 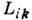 ,
к-рый выражается через временную корреляц. функцию динамич. переменных
,
к-рый выражается через временную корреляц. функцию динамич. переменных 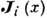 ,
соответствующих плотностям потоков компонентов:
,
соответствующих плотностям потоков компонентов:
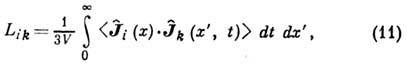
где усреднение ведётся
по локально равновесному состоянию, 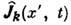 - значение
- значение  в
момент t при движении частиц i-й компоненты согласно Гамильтона
уравнению. Выражение
в
момент t при движении частиц i-й компоненты согласно Гамильтона
уравнению. Выражение 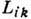 через корреляторы потоков Д. есть частный случай Грина - Кубо формул для
через корреляторы потоков Д. есть частный случай Грина - Кубо формул для
Д. В случае самодиффузии
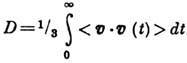 ,
,
где 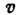 -
динамич. переменная скорости молекул. Расчёт коэфф. Д. с помощью ф-лы Грина
- Кубо очень сложен, однако он возможен с помощью ЭВМ. При выводе ф-лы Грина
- Кубо для Д. не делается к--л. предположений о характере теплового движения,
поэтому она справедлива для жидкостей, газов и твёрдых тел.
-
динамич. переменная скорости молекул. Расчёт коэфф. Д. с помощью ф-лы Грина
- Кубо очень сложен, однако он возможен с помощью ЭВМ. При выводе ф-лы Грина
- Кубо для Д. не делается к--л. предположений о характере теплового движения,
поэтому она справедлива для жидкостей, газов и твёрдых тел.
В жидкостях и газах возможен
эффект выравнивания пассивных примесей (не меняющих заметно обычного коэфф.
Д. и коэфф. вязкости) в турбулентном потоке (см. Турбулентная диффузия).
Диффузия в твёрдых телах.
Процесс Д. в твёрдых телах может осуществляться с помощью неск. механизмов:
обмен местами атомов кристаллич. структуры с её вакансиями ,перемещение
атомов по междоузлиям (см. Межузельный атом), одновременное циклическое
перемещение неск. атомов, обмен местами двух соседних атомов. При образовании
твёрдых растворов замещения преобладает обмен местами атомов и вакансий.
Коэф. Д. в твёрдых телах
очень зависит от дефектов структуры, увеличиваясь с ростом их числа. Для Д.
в твёрдых телах характерна экспоненц. зависимость от температуры с энергией активации
большей, чем у жидкостей. Коэф. Д. для цинка в медь возрастает в 1014 раз
при повышении температуры от 30оC до 300оC.
Микроскопич. теория Д.
атомов, основанная на механизме перескоков по вакансиям, была развита Я. И.
Френкелем [5]. Замещение атомом кристалич. структуры вакансии связано с возможностью
перехода его через потенц. барьер. Предполагается, что после перехода атома
в вакансию он благодаря сильному взаимодействию его с соседними атомами успевает
отдать часть энергии 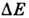 прежде, чем вернётся на своё прежнее место. Время пребывания данного атома в
соседнем с вакансией
узле равно
прежде, чем вернётся на своё прежнее место. Время пребывания данного атома в
соседнем с вакансией
узле равно
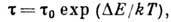
где  - время порядка периода колебаний атомов кристаллич. структуры, соответствующих
частоте акустич. спектра (
- время порядка периода колебаний атомов кристаллич. структуры, соответствующих
частоте акустич. спектра (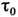 ~10-13
с). Тогда коэф. самодиффузии будет иметь вид
~10-13
с). Тогда коэф. самодиффузии будет иметь вид
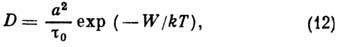
где 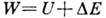 - энергия активации, а - постоянная решётки, U - энергия образования
вакансии. Для разл. решёток W отличаются не очень сильно (напр., для
свинца W
- энергия активации, а - постоянная решётки, U - энергия образования
вакансии. Для разл. решёток W отличаются не очень сильно (напр., для
свинца W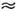 26
ккал/г*атом, для меди W
26
ккал/г*атом, для меди W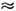 60
ккал/г*атом),а а и
60
ккал/г*атом),а а и 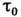 в ф-ле (12) могут сильно отличаться. Коэф. Д. в твёрдых телах можно оценить
также с помощью теории Эйринга скоростей реакций, что приводит также к экспоненц.
зависимости от температуры с энергией активации. Аналогичная теория была развита
для Д. в неупорядоченных сплавах замещения, она позволила учесть влияние внедрённых
атомов на самодиффузию металла, когда Д. уже не описывается одной экспонентой,
т. к. на узлах с разл. конфигурацией атомов нужно преодолевать разл. потенц.
барьеры. В том случае, когда Д. идёт путём обмена с вакансиями или одноврем.
перемещения по замкнутому контуру, причём коэф. Д. компонент D1 и D2 различны, появляется результирующий поток вещества
в направлении вещества с большим парциальным коэф. Д., пропорциональный
в ф-ле (12) могут сильно отличаться. Коэф. Д. в твёрдых телах можно оценить
также с помощью теории Эйринга скоростей реакций, что приводит также к экспоненц.
зависимости от температуры с энергией активации. Аналогичная теория была развита
для Д. в неупорядоченных сплавах замещения, она позволила учесть влияние внедрённых
атомов на самодиффузию металла, когда Д. уже не описывается одной экспонентой,
т. к. на узлах с разл. конфигурацией атомов нужно преодолевать разл. потенц.
барьеры. В том случае, когда Д. идёт путём обмена с вакансиями или одноврем.
перемещения по замкнутому контуру, причём коэф. Д. компонент D1 и D2 различны, появляется результирующий поток вещества
в направлении вещества с большим парциальным коэф. Д., пропорциональный 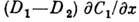 (Киркендалла эффект).
(Киркендалла эффект).
Явление переноса нейтронов
в конденсиров. среде, сопровождаемое многократным рассеянием, описывается кинетич.
ур-нием, к-рое, вообще говоря, не сводится к ур-нию Д., однако диффузионное
приближение оказывается часто полезным и при рассмотрении диффузии нейтронов.
При очень низких темп-pax
в конденсиров. средах возможна квантовая диффузия атомов, к-рая определяется
квантовым подбарьерным туннельным движением атомов, в отличие от классич. Д.,
к-рая определяется надбарьерными переходами атомов [9, 10]. Существ. отличие
квантовой Д. состоит в том, что коэф. квантовой Д. отличен от нуля при стремлении
температуры к нулю, его значение на мн. порядков больше, чем коэф. классич. Д. при
тех же температурах.
Другие виды диффузий.
К диффузионным процессам относят также нек-рые явления, не связанные с переносом
частиц. Так, в оптике имеет место явление переноса излучения в неоднородной
среде при многократных процессах испускания и поглощения фотонов, к-рое наз.
диффузией излучения, однако это явление существенно отлично от Д. частиц,
т. к. ур-ние баланса для плотности потока фотонов описывается интегр. ур-нием,
к-рое не сводится к дифференц. ур-нию Д. В спиновых системах в магн. поле возможен
процесс выравнивания ср. магн. момента в пространстве под влиянием спин-спинового
взаимодействия - спиновая диффузия.

Д. П. Зубарев
|
|