
Неопределённостей соотношения - фундаментальные соотношения квантовой механики, устанавливающие предел точности одноврем. определения
канонически-сопряжённых динамических переменных, характеризующих квантовую систему:
координата - импульс, действие - угол и т. д. Математически Н. с. имеет вид
неравенства, напр.

где Dх
и Dрх
- неопределённости значений координаты х и сопряжённой ей компоненты
рх импульса р (аналогичные соотношения справедливы
и для пар др. компонент координаты и импульса: у, ру; z, pz).
Н. с. были установлены В. Гейзенбергом (W. Heisen-berg)
в 1927 при анализе мысленного эксперимента по измерению
координаты квантового объекта с помощью "гамма-микроскопа" [1].
В 1929 X. П. Робертсон (Н. P. Robertson) показал, что Н. с.
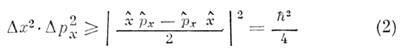
являются следствием коммутац. соотношений (см.
Перестановочные соотношения) 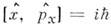 между операторами
между операторами 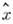 и
и 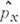 соответствующих
физ. величин, причём Dx
и Dрx
в (1) определяются как среднеквадратичные отклонения:
соответствующих
физ. величин, причём Dx
и Dрx
в (1) определяются как среднеквадратичные отклонения:

где чертой обозначены средние от операторов,
определяемые ф-лои

(y
- волновая функция состояния, интегрирование производится по всему объёму,
где y 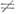 0;
звёздочкой помечено комплексное сопряжение). Он же доказал, что равенство в
H. с..достигается только для квантовых состояний, к-рые описываются т. н. гауссовыми
волновыми пакетами (см. Когерентное состояние ).Э. Шрёдингер (Е.
Schrodinger) предложил более общую ф-лу в случае т. н. коррелпров. состояний
[2], для к-рых
0;
звёздочкой помечено комплексное сопряжение). Он же доказал, что равенство в
H. с..достигается только для квантовых состояний, к-рые описываются т. н. гауссовыми
волновыми пакетами (см. Когерентное состояние ).Э. Шрёдингер (Е.
Schrodinger) предложил более общую ф-лу в случае т. н. коррелпров. состояний
[2], для к-рых
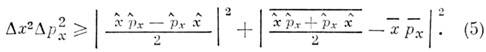
Если ввести коэф. корреляции r2,
равный отношению второго члена правой части к произведению Dх2.Dр2х, то Н. с. (5) примет вид
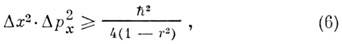
т. е. для сильно коррелированных состояний (r ~ 1) "эфф. постоянная Планка"
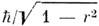 может существенно
превышать величину
может существенно
превышать величину 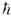 .
.
Соотношения типа (1) имеют место для любых физ.
величин (f, g), к-рым соответствуют некоммутирующие эрмитовы операторы.
Если коммутатор  (где
(где 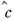 - эрмитов
оператор), то Н. с. приобретают вид
- эрмитов
оператор), то Н. с. приобретают вид
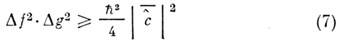
[к-рый для коррелиров. состояний модифицируется
аналогично (6)]. В частности, для проекций угл. момента 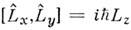 , и поэтому
, и поэтому
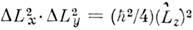
Среди физ. толкований Н. с. можно выделить по
крайней мере три уровня, к-рым в англоязычной литературе соответствуют три разл.
термина: uncertainty, indeterminateness, indeterminancy. Наиб. часто, особенно
в упрощённых изложениях принципов квантовой механики, Н. с. (uncertainty relations)
трактуют как ограничение на экспериментально достижимую точность измерения характеристик
квантовых объектов, обусловленное неадекватностью классич. приборов целям квантовых
измерений.
Др. толкование (indeterminateness) исходит из
предпосылки, что Н. с. есть следствие свойства квантовых объектов, внутренне
присущих им, независимо от несовершенства конкретных реализаций эксперим. установок,
предназначенных для измерения этих свойств. Таким внутр. свойством является
корпускулярно-волно-вой дуализм квантовых объектов, т. е. неразделимое
сочетание волновых и корпускулярных свойств, равно необходимых для их полного
описания. С этой точки зрения, аналоги Н. с. были хорошо известны, напр. в акустике
и оптике, задолго до создания квантовой механики. Так, для цуга излучения протяжённостью
Dх, представляющего
собой волновой пакет с волновыми числами,
лежащими в интервале Dk,
справедливы соотношения

к-рые с учётом квантового соотношения де Бройля
р =  k эквивалентны Н. с. (1).
k эквивалентны Н. с. (1).
Второе толкование Н. с. значительно шире и плодотворнее
первого, поскольку оно представляет собой не частное утверждение о границах
уточнения характеристик квантовых объектов, а гораздо более общий принцип неопределённости.
Этот принцип по существу является предпосылкой статистич. интерпретации квантовой
механики и важнейшим примером дополнительности принципа Бора (для этого
расширит. толкования Н. с. часто используют термин indeterminancy). С точки
зрения этого более общего принципа, Н. с. трактуются как способ сохранить клас-сич.
понятия для описания квантовых систем путём взаимного ограничения области их
совместной применимости.
Н. с. для энергии 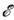 и времени t по форме совпадает с (1):
и времени t по форме совпадает с (1):

однако их толкование отличается от интерпретации
соотношения (1). Обычно Н. с. (9) трактуются как невозможность точного определения
энергии квантовой системы (D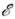 = 0) за ограниченный интервал времени Dt.
В качестве иллюстрации Н. с. для пары
= 0) за ограниченный интервал времени Dt.
В качестве иллюстрации Н. с. для пары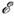 и
t H. Бор (N. Bohr) обращал внимание на невозможность определить понятие
монохроматич. волны в данный момент времени.
и
t H. Бор (N. Bohr) обращал внимание на невозможность определить понятие
монохроматич. волны в данный момент времени.
Другая трактовка Н. с. (9) тесно связана с понятием
квазистационарного состояния. В этом случае D - неопределённость значения, к-рое приобретает энергия
- неопределённость значения, к-рое приобретает энергия  , рассматривающаяся как динамическая характеристика квантовой системы, изменяющаяся
во времени, а Dt
- интервал времени, характеризующий эволюцию
, рассматривающаяся как динамическая характеристика квантовой системы, изменяющаяся
во времени, а Dt
- интервал времени, характеризующий эволюцию 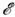 в интервале значений D
в интервале значений D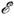 .
Для возбуждённых квантовых систем (напр., атома или молекулы) неопределённость
энергии состояния D
.
Для возбуждённых квантовых систем (напр., атома или молекулы) неопределённость
энергии состояния D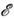 (естеств. ширина уровня) непосредственно связана с его временем жизни с помощью
Н. с. (9). (Это утверждение строго следует из теоремы Фока и Крылова [3].)
(естеств. ширина уровня) непосредственно связана с его временем жизни с помощью
Н. с. (9). (Это утверждение строго следует из теоремы Фока и Крылова [3].)
Благодаря существованию Н. с. (9) возможны виртуальные
переходы, происходящие с нарушением 2-го постулата Бора, т. е. с энергиями 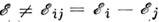 ,
где
,
где 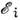 и
и 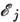 - энергии начального (i)и конечного (j) состояний квантовой системы.
При этом время жизни квантовой системы Dt
определяется из соотношения (9), в к-ром
- энергии начального (i)и конечного (j) состояний квантовой системы.
При этом время жизни квантовой системы Dt
определяется из соотношения (9), в к-ром  .
Виртуальные переходы могут происходить как с недостатком (D
.
Виртуальные переходы могут происходить как с недостатком (D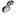 < 0), так и с избытком (D
< 0), так и с избытком (D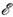 > 0) энергии
> 0) энергии 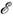 по сравнению с энергией идеального перехода
по сравнению с энергией идеального перехода 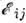 ,
причём это имеет место как при испускании, так и при поглощении энергии квантовой
системой. В частности, эта энергия может поглощаться и испускаться в виде фотонов.
В этом случае виртуальное поглощение или испускание фотонов лежит в основе многофотонных
процессов (напр., многофотонной ионизации)в квантовых системах.
,
причём это имеет место как при испускании, так и при поглощении энергии квантовой
системой. В частности, эта энергия может поглощаться и испускаться в виде фотонов.
В этом случае виртуальное поглощение или испускание фотонов лежит в основе многофотонных
процессов (напр., многофотонной ионизации)в квантовых системах.
Соотношения неопределённостей являются не только важной составной частью
понятийного базиса квантовой механики, но они дают также способ для простых
оценок количественных характеристик квантовых систем. Напр., исходя из известных
размеров атома водорода, а = 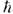 2/те2, и соотношения (1), можно оценить характерную скорость атомного электрона
в осн. состоянии: u
>= Dр/m
~ ~
2/те2, и соотношения (1), можно оценить характерную скорость атомного электрона
в осн. состоянии: u
>= Dр/m
~ ~ 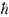 /та ~
е2/
/та ~
е2/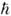 , т. е. u/c
, т. е. u/c 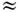 е2/
е2/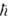 с
с 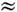 a
a
 1/137 (т и е - масса и заряд электрона).
1/137 (т и е - масса и заряд электрона).
Для ограниченных в объёме квантовых систем из соотношений неопределённостей следует также существование энергии нулевых колебаний систем (см. Нулевая энергия, Нулевые колебания).

Л. И. Пономарёв
|
|