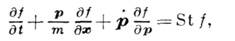
Кинетика физическая - микроскопич. теория процессов в неравновесных средах.
В Физической кинетике методами квантовой или классич. статистической физики изучают процессы
переноса энергии, импульса, заряда и вещества в разл. физ. системах (газах,
плазме, жидкостях, твёрдых телах) и влияние на них внеш. полей.
В отличие от термодинамики неравновесных процессов и электродинамики сплошных сред, К. ф. исходит из представления о молекулярном строении рассматриваемых сред, что позволяет вычислить из первых принципов кинетические коэффициенты ,диэлектрич. и магн. проницаемости и др. характеристики сплошных сред.
Физическая кинетика включает в себя кинетическую
теорию газов из нейтральных атомов или молекул, статистич. теорию неравновесных
процессов в плазме, теорию явлений переноса в твёрдых телах (диэлектриках, металлах
и полупроводниках) и жидкостях, кинетику магн. процессов и теорию кинетич. явлений,
связанных с прохождением быстрых частиц через вещество. К ней же относятся теория
процессов переноса в квантовых жидкостях и сверхпроводниках и кинетика
фазовых переходов.
Если известна функция распределения
всех частиц системы по их координатам и импульсам в зависимости от времени (в
квантовом случае - статистич. оператор), то можно вычислить все характеристики
неравновесной системы. Вычисление полной функции распределения является практически
неразрешимой задачей, но для определения мн. свойств физ. систем, напр. потока
энергии или импульса, достаточно знать функцию распределения небольшого числа
частиц, а для газов малой плотности - одной частицы.
В физической кинетике используется существ. различие времён релаксации в неравновесных процессах (иерархия времён релаксации), напр. для газа из частиц или квазичастиц время свободного пробега значительно больше времени столкновения между частицами. Это позволяет перейти от полного описания неравновесного состояния функцией распределения по всем координатам и импульсам к сокращённому описанию при помощи функции распределения одной частицы по её координатам и импульсам.
Кинетическое уравнение. Осн. метод К. ф. - решение кинетического уравнения Больцмана для
одночастичной функции распределения f(x, р, t)
молекул в фазовом пространстве их координат x и импульсов р.
функция распределения удовлетворяет кинетич. ур-нию
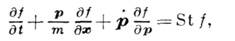
где Stf - интеграл
столкновений, определяющий разность числа частиц, приходящих в элемент объёма
вследствие прямых столкновений и убывающих из него вследствие обратных столкновений.
Для одноатомных молекул или для многоатомных, но без учёта их внутр. степеней
свободы
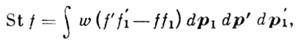
где 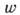 - вероятность столкновения, связанная с диф-ференц. эфф. сечением рассеяния
da:
- вероятность столкновения, связанная с диф-ференц. эфф. сечением рассеяния
da:

где р, р1
- импульсы молекул до столкновения, v, v1
- соответств. скорости, 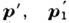 - их импульсы после столкновения, f, f1 - функции распределения
молекул до столкновения,
- их импульсы после столкновения, f, f1 - функции распределения
молекул до столкновения,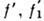 - их функции распределения после столкновения. Для газа из сложных молекул, обладающих
внутр. степенями свободы, их следует учитывать в функции распределения. Напр.,
для двухатомных молекул с собств. моментом вращения М функции распределения
будут зависеть также от М.
- их функции распределения после столкновения. Для газа из сложных молекул, обладающих
внутр. степенями свободы, их следует учитывать в функции распределения. Напр.,
для двухатомных молекул с собств. моментом вращения М функции распределения
будут зависеть также от М.
Из кинетич. ур-ния следует
Больцмана Н-теорема - убывание со временем Я-функции Больцмана (ср. логарифма
функции распределения) или возрастание энтропии, т. к. она равна Я-функции Больцмана
с обратным знаком.
Уравнения переноса. К. ф. позволяет получить ур-ния баланса ср. плотностей вещества, импульса
и энергии. Напр., для простого газа плотность 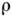 ,
гидро-динамич. скорость V и ср. энергия
,
гидро-динамич. скорость V и ср. энергия 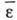 удовлетворяют ур-ниям баланса:
удовлетворяют ур-ниям баланса:
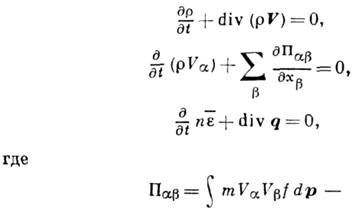
тензор плотности потока
импульса, п - плотность числа частиц, 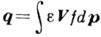 - плотность потока энергии.
- плотность потока энергии.
Если состояние газа мало
отличается от равновесного, то в малых элементах объёма устанавливается распределение,
близкое к локально равновесному Максвелла распределению,
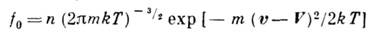
с температурой, плотностью
и гидродинамич. скоростью, соответствующими рассматриваемой точке газа. В этом
случае неравновесная функция распределения мало отличается от локально равновесной
и решение кинетич.
ур-ния даёт малую поправку
к последней, пропорциональную градиентам температуры 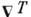 и гидродинамич. скорости
и гидродинамич. скорости 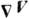 ,
т. к.
,
т. к. 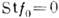 .С
помощью неравновесной функции распределения можно найти поток энергии (в неподвижной
жидкости)
.С
помощью неравновесной функции распределения можно найти поток энергии (в неподвижной
жидкости) 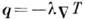 ,
где
,
где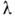 - коэф. теплопроводности, и тензор плотности потока импульса
- коэф. теплопроводности, и тензор плотности потока импульса

где
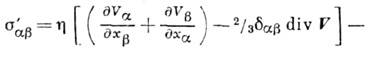
тензор вязких напряжении,
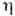 - коэф.
сдвиговой вязкости, Р- давление. Для газов с внутр. степенями свободы
- коэф.
сдвиговой вязкости, Р- давление. Для газов с внутр. степенями свободы
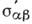 содержит
также член
содержит
также член 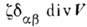 ,
где
,
где 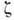 - коэф. "второй", объёмной вязкости, проявляющейся лишь при движениях,
в к-рых
- коэф. "второй", объёмной вязкости, проявляющейся лишь при движениях,
в к-рых 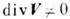 .
Для кинетич. коэффициентов
.
Для кинетич. коэффициентов 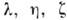 получаются выражения через эфф. сечения столкновений и, следовательно, через
константы молекулярных взаимодействий. В бинарной смеси поток вещества состоит
из диффуз. потока, пропорционального градиенту концентрации вещества в смеси
с коэф. диффузии, и термодиффузионного потока, пропорционального градиенту температуры
с коэф. термодиффузии, а поток тепла, кроме обычного члена теплопроводности,
пропорционального градиенту температуры, содержит дополнит. член, пропорциональный
градиенту концентрации и описывающий Дюфура эффект .К. ф. даёт выражения
для этих кинетич. коэффициентов через эфф. сечения столкновений. Кинетич. коэффициенты
для перекрёстных явлений, напр. термодиффузии и эффекта Дюфура, оказываются
равными (Онсагера теорема ).Эти соотношения являются следствием микро-скопич.
обратимости ур-ний движения частиц системы, т. е. инвариантности их относительно
обращения времени.
получаются выражения через эфф. сечения столкновений и, следовательно, через
константы молекулярных взаимодействий. В бинарной смеси поток вещества состоит
из диффуз. потока, пропорционального градиенту концентрации вещества в смеси
с коэф. диффузии, и термодиффузионного потока, пропорционального градиенту температуры
с коэф. термодиффузии, а поток тепла, кроме обычного члена теплопроводности,
пропорционального градиенту температуры, содержит дополнит. член, пропорциональный
градиенту концентрации и описывающий Дюфура эффект .К. ф. даёт выражения
для этих кинетич. коэффициентов через эфф. сечения столкновений. Кинетич. коэффициенты
для перекрёстных явлений, напр. термодиффузии и эффекта Дюфура, оказываются
равными (Онсагера теорема ).Эти соотношения являются следствием микро-скопич.
обратимости ур-ний движения частиц системы, т. е. инвариантности их относительно
обращения времени.
Ур-ние баланса импульса
с учётом выражения для плотности потока импульса через градиент скорости даёт
Навье-Стокса уравнения, ур-ние баланса энергии с учётом выражения для
плотности потока тепла даёт теплопроводности ур-ние, ур-ние баланса числа частиц
определ. сорта с учётом выражения для диффуз. потока даёт диффузии уравнение. Такой гидродинамич. подход справедлив, если длина свободного пробега l значительно меньше характерных размеров областей неоднородности.
Газы и плазма. К. ф. позволяет
исследовать явления переноса в разреж. газах, когда отношение длины свободного
пробега l к характерным размерам задачи L (т. е. Кнудсена число
l/L)уже не очень мало и имеет смысл рассматривать поправки порядка l/L (слабо разреж. газы). В этом случае К. ф. объясняет явления температурного
скачка и течения газов вблизи твёрдых поверхностей.
Для сильно разреж. газов,
когда l/L>1, гидродинамич. ур-ния и обычное ур-ние теплопроводности
уже не применимы и для исследования процессов переноса необходимо решать кинетич.
ур-ние с определ. граничными условиями на поверхностях, ограничивающих газ.
Эти условия выражаются через функцию распределения молекул, рассеянных из-за взаимодействия
со стенкой. Рассеянный поток частиц может приходить в тепловое равновесие со
стенкой, но в реальных случаях это не достигается. Для сильно разреж. газов
роль коэф. теплопроводности играют коэф. теплопередачи. Напр., кол-во тепла
Q, отнесённое к единице площади параллельных пластинок, между к-рыми
находится разреж. газ, равно 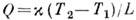 , где Т1 и Т2 - теми-ры пластинок, L - расстояние между ними,
, где Т1 и Т2 - теми-ры пластинок, L - расстояние между ними, 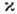 - коэф. теплопередачи.
- коэф. теплопередачи.
Теория явлений переноса в плотных газах и жидкостях значительно сложнее, т. к. для описания неравновесного
состояния уже недостаточно одночастичной функции распределения, а нужно учитывать
функции распределения более высокого
порядка Частичные функции распределения удовлетворяют цепочке зацепляющихся ур-ний
(Боголюбова уравнений, наз. также цепочкой ББГКИ, т. е. ур-ний Боголюбова-Борна-Грина-
Кирквуда-Ивона). С помощью этих ур-ний можно уточнить кинетич. ур-ние для газов
ср. плотности и исследовать для них явления переноса.
Физическая кинетика двухкомпонентной
плазмы описыпается двумя функциями распределения (для электронов 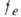 ,
для ионов fi) удовлетворяющими системе двух кинетич. ур-ний.
На частицы плазмы действуют силы
,
для ионов fi) удовлетворяющими системе двух кинетич. ур-ний.
На частицы плазмы действуют силы
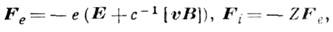
где Ze - заряд иона,
Е - напряжённость электрич. поля, В- магн. индукция,
удовлетворяющие Максвелла уравнениям .Ур-ния Максвелла содержат ср. плотности
тока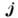 и заряда
и заряда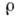 ,
определяемые с помощью функций распределения:
,
определяемые с помощью функций распределения:
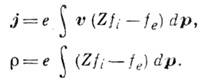
Т. о., кинетич. ур-ния
и yp-ния Максвелла образуют связанную систему ур-ний, определяющих все неравновесные
явления в плазме. Такой подход наз. приближением самосогласованного поля. При
этом столкновения между электронами учитываются не явно, а лишь через создаваемое
ими самосогласованное поле (см. Кинетические уравнения для плазмы). При
учёте столкновений электронов возникает кинетич.. ур-ние, в к-ром эфф. сечение
столкновений очень медленно убывает с ростом прицельного расстояния, становятся
существенными столкновения с малой передачей импульса, в интеграле столкновений
появляется логарифмич. расходимость. Учёт эффектов экранирования позволяет избежать
этой трудности.
Физическая кинетика неравновесных процессов в диэлектриках основана на решении кинетич. ур-ния Больцмана для фононов решётки (ур-ние Пайерлса). Взаимодействие между фононами вызвано членами гамильтониана решётки, ангармоническими относительно смещения атомов на положения равновесия. При простейших столкновениях один фонон распадается на два или происходит слияние двух фононов в один, причём сумма их квазиимпульсов либо сохраняется (нормальные процессы столкновений), либо меняется на вектор обратной решётки (процессы переброса). Конечная теплопроводность возникает при учёте процессов переброса. При низких температурах, когда длина свободного пробега больше размеров образца L, роль длины свободного пробега играет L. Кинетич. ур-ние для фононов позволяет исследовать теплопроводность и поглощение звука в диэлектриках. Если длина свободного пробега для нормальных процессов значительно меньше длины свободного пробега для процессов переброса, то система фопонов в кристалле при низких темп-pax подобна обычному газу. Нормальные столкновения устанавливают внутр. равновесие в каждом элементе объёма газа, к-рый может двигаться со скоростью V, мало меняющейся на длине свободного пробега для нормальных столкновении. Поэтому можно построить ур-ния гидродинамики фононного газа в диэлектрике. К. ф. м е т а л л о в основана на решении кинетич. ур-ния для электронов, взаимодействующих с колебаниями кристаллич. решётки. Электроны рассеиваются на колебаниях атомов решётки, примесях и дефектах, нарушающих её периодичность, причём возможны как нормальные столкновения, так и процессы переброса. Электрич. сопротивление возникает в результате этих столкновений. К. ф. объясняет термоэле-ктрич., гальваномагн, и термомагн. явления, скин-эффект, циклотронный резонанс в ВЧ-полях и др. кинетич. эффекты в металлах. Для сверхпроводников она объясняет особенности их ВЧ-поведения.
Физическая кинетика магнитных явлений основана
на решении кинетич. ур-ния для магнонов. Она позволяет вычислить динамич. восприимчивости
магн. систем в перем. полях, изучить кинетику процессов намагничивания.
Физическая кинетика явлений при прохождении
быстрых частиц через вещество основана на решении системы кинетич. ур-ний для
быстрых частиц и вторичных частиц, возникающих при столкновениях, напр, для
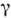 -лучей (фотонов)
с учётом разл. процессов в среде (фотоэффекта, комптоновского рассеяния, образования
пар). В этом случае К. ф. позволяет вычислить коэф. поглощения и рассеяния быстрых
частиц.
-лучей (фотонов)
с учётом разл. процессов в среде (фотоэффекта, комптоновского рассеяния, образования
пар). В этом случае К. ф. позволяет вычислить коэф. поглощения и рассеяния быстрых
частиц.
Фазовые переходы. К.ф.
фазовых переходов первого рода, т. е. со скачком энтропии, связана с образованием
и ростом зародышей новой фазы. функция распределения зародышей по нх размерам
(если зародыши считать макроскопич. образованиями, а процесс роста - медленным)
удовлетворяет Фоккера-Планка уравнению:
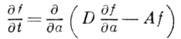
где а - радиус зародыша,
D - "коэф. диффузии зародышей по размерам", А пропорционально
мин. работе, к-рую нужно затратить на создание зародыша данного размера. К.
ф. фазовых переходов 2-го рода в наиб. простом приближении основана на ур-нии
релаксации параметра порядка 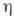 ,
характеризующего степень упорядоченности, возникающей при фазовом переходе:
,
характеризующего степень упорядоченности, возникающей при фазовом переходе:
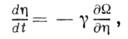
где 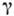 - постоянный коэф.,
- постоянный коэф., 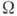 - термодинамич. потенциал в переменных Т и
- термодинамич. потенциал в переменных Т и 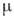 (
(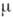 - хим. потенциал),
вблизи точки фазового перехода зависящий от
- хим. потенциал),
вблизи точки фазового перехода зависящий от 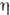 .
Для этой зависимости используется разложение по степеням
.
Для этой зависимости используется разложение по степеням 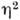 и Т-Т с, где Тс - темп-pa фазового перехода.
(См. также Кинетика фазовых переходов.)
и Т-Т с, где Тс - темп-pa фазового перехода.
(См. также Кинетика фазовых переходов.)
Явления переноса в жидкостях.
Теорию явлений переноса в жидкостях также можно отнести к К. ф., хотя для жидкостей
метод кинетич. ур-ний непригоден, но для них возможен более общий подход, основанный
также на иерархии времён релаксации. Для жидкости время установления равновесия
в макроскопически малых (но содержащих ещё большое число молекул) элементарных
объёмах значительно больше, чем время релаксации во всей системе, вследствие
чего в малых элементах объёма приближённо устанавливается статистич. равновесие.
Поэтому в качестве исходного приближения при решении Лиувилля уравнения можно
принять локально равновесное Гиббса распределение с температурой Т (x,
t), хим. потенциалом 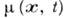 и гидродинамич. скоростью F(x, t), соответствующими рассматриваемой
точке жидкости. Напр., для однокомпонентной жидкости локально равновесная функция
распределения (или статистич. оператор) имеет вид
и гидродинамич. скоростью F(x, t), соответствующими рассматриваемой
точке жидкости. Напр., для однокомпонентной жидкости локально равновесная функция
распределения (или статистич. оператор) имеет вид
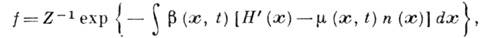
где
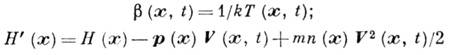
- плотность энергии в системе
координат, движущейся вместе с элементом жидкости, Н (х)- плотность
энергии в неподвижной системе координат, р (х) - плотность импульса,
n(x) - плотность числа частиц, рассматриваемые как фазовые функции, т.
е. функции от координат и
импульсов всех частиц, напр.
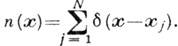
Приближённое решение ур-ния
Лиувилля для состояний, близких к статистически равновесному, позволяет вывести
ур-ния теплопроводности и Навье-Стокса для
жидкости и получить микроскопич. выражения для кинетич. коэф. теплопроводности
и вязкости через пространственно-временные корреляц. функции плотностей потоков
энергии и импульсов всех частиц системы (Грина-Кубо формулы). Этот же
подход возможен и для смеси жидкостей. Подобное решение ур-ния Лиувилля есть
его частное решение, зависящее от времени лишь через параметры 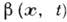 ,
,  , V(x,
t), соответствующие сокращённому гидродинамич. описанию неравновесного состояния
системы, к-рое справедливо, когда все гидродинамич. параметры мало меняются
на расстояниях порядка длины свободного пробега (для газов) или длины корреляций
потоков энергии или импульса (для жидкостей). [В квантовом случае Я (ж), р(x),
п(x) - операторы в представлении вторичного квантования.]
, V(x,
t), соответствующие сокращённому гидродинамич. описанию неравновесного состояния
системы, к-рое справедливо, когда все гидродинамич. параметры мало меняются
на расстояниях порядка длины свободного пробега (для газов) или длины корреляций
потоков энергии или импульса (для жидкостей). [В квантовом случае Я (ж), р(x),
п(x) - операторы в представлении вторичного квантования.]
К задачам физической кинетики относится также вычисление обобщённой восприимчивости, выражающей линейную реакцию
физ. системы на включение внеш. поля. Её можно выразить через Грина функции с усреднением по состоянию, к-рое может быть и неравновесным.
В физической кинетике исследуют также кинетич. свойства квантовых систем, что требует применения метода матрицы плотности (см., напр., Кинетическое уравнение основное).

Д. Н. Зубарев.
|
|