Кинетика фазовых переходов - раздел кинетики физической, в к-ром исследуют
процессы возникновения новой фазы при фазовых превращениях. Эти процессы различны
для фазовых переходов (ФП) 1-го
и 2-го рода, поскольку в случае ФП 1-го рода фазы резко отличаются друг от друга,
тогда как в случае ФП 2-го
рода они почти совпадают.
Фазовый переход 1-го
рода. Превращение одной фазы в др. при ФП 1-го рода требует перестройки
системы и преодоления барьера энергетически невыгодных промежуточных состояний.
Благодаря этому возможно существование метастабильного состояния старой
фазы в области, где абсолютно устойчивой является новая фаза. Метастабильное
состояние системы за конечное время превращается в устойчивое в результате процесса
флуктуац. возникновения небольших областей новой фазы - зародышей. В первой
стадии процесса их число невелико, каждый зародыш растёт независимо от др.,
эту стадию наз. нуклеацией. В последующей стадии происходит рост и объединение
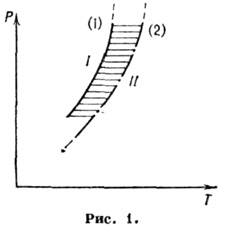
областей новой фазы. На фазовой диаграмме (рис. 1) линия ФП (1) разделяет области
давлений Р и температур Т, где фазы I и II стабильны. Область существования
метастабильной фазы I заштрихована.

При переходе системы N частиц из метастабильного состояния
в стабильное энергетич. выигрыш составляет 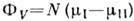 , где
, где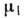 и
и
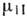 - хим.
потенциалы частиц в I и II фазах как функции Т и Р. Линия ФП определяется
условием
- хим.
потенциалы частиц в I и II фазах как функции Т и Р. Линия ФП определяется
условием 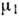 (Р,
Т)--
(Р,
Т)--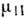 (Р,
Т). Зародыш имеет такую же
плотность числа частиц п, как и стабильная фаза II, а объём
(Р,
Т). Зародыш имеет такую же
плотность числа частиц п, как и стабильная фаза II, а объём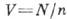 . Энергетич. затраты ФS на образование поверхности пропорциональны
числу частиц на поверхности:
. Энергетич. затраты ФS на образование поверхности пропорциональны
числу частиц на поверхности: 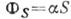 ,
энергия образования поверхности единичной площади а наз. коэф. поверхностного
натяжения. Для изотропных фаз мин. поверхность
,
энергия образования поверхности единичной площади а наз. коэф. поверхностного
натяжения. Для изотропных фаз мин. поверхность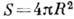 при заданном объёме
при заданном объёме 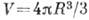 имеет сферич. зародыш радиуса R. Общее изменение энергии Ф(Р, Т; R)
для такого зародыша равно
имеет сферич. зародыш радиуса R. Общее изменение энергии Ф(Р, Т; R)
для такого зародыша равно
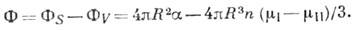
Зародыш малого размера
энергетически невыгоден из-за относительно большой поверхности, функция Ф(R) имеет
максимум при R==RС, 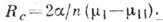 Зародыш радиуса Rc наз. критическим. Вблизи линии ФП разность
Зародыш радиуса Rc наз. критическим. Вблизи линии ФП разность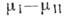 мала
и размер Rc велик по сравнению с межатомным.
мала
и размер Rc велик по сравнению с межатомным.
Энергия 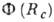 определяет мин. высоту барьера, к-рый необходимо преодолеть для перехода из
метаста-бильной фазы в стабильную. Вероятность флуктуац. образования критич.
зародыша
определяет мин. высоту барьера, к-рый необходимо преодолеть для перехода из
метаста-бильной фазы в стабильную. Вероятность флуктуац. образования критич.
зародыша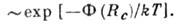
Этой же величине пропорционально
время жизни метас-табильного состояния. Для более точного анализа необходимо
кинетич. рассмотрение процесса нуклеации. Изменение размеров зародышей рассматривают
как результат случайных присоединений и отрывов частиц от зародыша новой фазы.
В среднем такое броуновское движение приводит к уменьшению величины Ф(R), т.
е. к уменьшению зародышей с размером, меньшим критического, и к увеличению зародышей
размера больше Rс. За счёт флуктуации возможен с малой вероятностью
рост малого зародыша до размера Rс, после чего с подавляющей вероятностью
этот зародыш будет про-должать расти. В области малых размеров вероятность рождения
докритич. зародышей велика. Диффузия зародышей по размерам из области 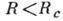 приводит к потоку 1 зародышей в область закритич. размеров. Число зародышей,
переходящих в единицу времени в область закритич. размеров, в единице объёма
системы равно
приводит к потоку 1 зародышей в область закритич. размеров. Число зародышей,
переходящих в единицу времени в область закритич. размеров, в единице объёма
системы равно 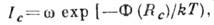 предэкспоненц. фактор
предэкспоненц. фактор 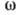 зависит от кинетич. характеристик системы.
зависит от кинетич. характеристик системы.
При удалении от линии ФП
высота барьера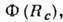 размер критич. зародыша и время жизни метастабиль-ного состояния уменьшаются.
Для описания зародышей атомных размеров требуется микроскопич. подход. Ме-тастабильные
состояния переходят в нестабильные на спинодали - линии абс. неустойчивости
[линии (2) на рис. 1]. Вблизи этой линии характер зародыша изменяется. Критич.
зародыш здесь имеет форму и размер, зависящие от близости к спинодали.
размер критич. зародыша и время жизни метастабиль-ного состояния уменьшаются.
Для описания зародышей атомных размеров требуется микроскопич. подход. Ме-тастабильные
состояния переходят в нестабильные на спинодали - линии абс. неустойчивости
[линии (2) на рис. 1]. Вблизи этой линии характер зародыша изменяется. Критич.
зародыш здесь имеет форму и размер, зависящие от близости к спинодали.
По мере появления и роста
зародышей степень мета-стабильности нач. фазы падает. Это приводит к увеличению
критич. размера зародышей Rc и уменьшению вероятности их возникновения.
Мелкие зародыши становятся неустойчивыми и исчезают. Определяющую роль на этой
стадии приобретает процесс роста крупных зародышей за счёт "поедания"
мелких (процесс коалесценции). В случае выпадения растворённого вещества из
пересыщ. твёрдого раствора зародыши в целом неподвижны и растут только за счёт
диф-фуз. подвода вещества. При малой нач. концентрации раствора, когда непосредств.
взаимодействием зародышей можно пренебречь, можно найти асимптотич. временные
зависимости критич. размера зародыша Rс, полного числа зародышей
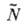 и степени пересыщения раствора
и степени пересыщения раствора 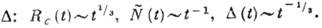 функция распределения зародышей по размерам
функция распределения зародышей по размерам 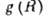 имеет автомодельный вид:
имеет автомодельный вид: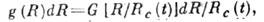 где
где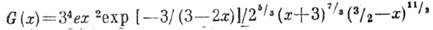 при
при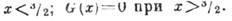 Для процесса коалесценции в жидкой фазе определяющим является непосредств. слияние
зародышей, участвующих в гидроди-намич. движениях. В этом случае временные зависимости
и функция распределения зародышей определяются др. выражениями.
Для процесса коалесценции в жидкой фазе определяющим является непосредств. слияние
зародышей, участвующих в гидроди-намич. движениях. В этом случае временные зависимости
и функция распределения зародышей определяются др. выражениями.
Реальные процессы нуклеации
и коалесценции обладают рядом особенностей по сравнению с рассмотренной простейшей
моделью. Так, при ФП 1-го рода в кристаллах и жидких кристаллах необходимо учитывать
влияние анизотропии, а также энергии упругой деформации, что может приводить
к существ. изменению результатов для размера и вероятности возникновения критич.
зародыша. На процесс роста зародышей в твёрдой (или жидкокристаллич.) фазе существенно
влияет присутствие даже малых концентраций дефектов, к-рые тормозят движение
межфазных границ, так что рост зародышей достаточно большого размера оказывается
экспоненциально медленным. В жидкостях скорость образования критич. зародышей
обычно определяется присутствием разл. рода посторонних включений, к-рые служат
центрами образования новой фазы, что существенно ускоряет процесс ФП. В ряде
случаев, напр, при конденсации насыщ. пара, соприкасающегося со стенками сосуда,
полностью смачиваемыми данной жидкостью, ФП происходит без образования зародышей.
В таких случаях существование метастабильной фазы невозможно.
Фазовый переход 2-го рода.
К. ф. п. в этом случае определяется медленной релаксацией параметра порядка
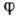 к
своему равновесному значению. Обычно предполагают, что процесс релаксации носит
чисто диссипативный характер, при этом скорость изменения параметра
к
своему равновесному значению. Обычно предполагают, что процесс релаксации носит
чисто диссипативный характер, при этом скорость изменения параметра 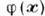 пропорц. обобщённой силе
пропорц. обобщённой силе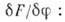
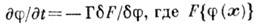 - функционал свободной энергии (см. квантовая теория), Г - кинетич. коэф. Простейшее приближение критич. динамики получится,
если пренебречь пространств, флуктуациями параметра порядка, а кинетич. коэф.
Г считать пост. величиной, не изменяющейся при приближении к критической
точке Тс. В результате особенность времени релаксации tc вблизи Тс для параметра порядка совпадает с особенностью
обобщённой восприимчивости
- функционал свободной энергии (см. квантовая теория), Г - кинетич. коэф. Простейшее приближение критич. динамики получится,
если пренебречь пространств, флуктуациями параметра порядка, а кинетич. коэф.
Г считать пост. величиной, не изменяющейся при приближении к критической
точке Тс. В результате особенность времени релаксации tc вблизи Тс для параметра порядка совпадает с особенностью
обобщённой восприимчивости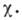
Общий подход к критич.
динамике, при к-ром особенности динамич. величин выражаются через термо-динамич.
критические показатели ,наз. динамич. масштабной инвариантностью. Конкретное
применение этого подхода, как и вообще К. ф. п. 2-го рода, существенно зависит
от существования в системе гидроди-намич. голдстоуновских мод (степеней
свободы), характеризуемых локальными значениями термодинамич. параметров (температуры,
давления, плотности п др.), а также скорости, меняющихся в пространстве и во
времени. Гидродинамич. подход оправдан тогда, когда характерные масштабы 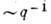 и времена
и времена 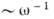 движений
велики по сравнению со статич. радиусом корреляции rс и временем
релаксации флуктуации tc. В окрестности ФП величины rс и tc растут, а область применимости гидродинамики сужается.
Движения в области
движений
велики по сравнению со статич. радиусом корреляции rс и временем
релаксации флуктуации tc. В окрестности ФП величины rс и tc растут, а область применимости гидродинамики сужается.
Движения в области 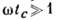 не имеют гидродинамич. характера, они
не имеют гидродинамич. характера, они 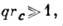 не зависят от величины
не зависят от величины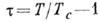 ,
а мнимая часть частоты не меньше действительной. Такие движения наз. флуктуационными.
Согласно гипотезе динамич. масштабной инвариантности, характерные частоты гидродинамич.
и флуктуац. мод можно описать единым образом:
,
а мнимая часть частоты не меньше действительной. Такие движения наз. флуктуационными.
Согласно гипотезе динамич. масштабной инвариантности, характерные частоты гидродинамич.
и флуктуац. мод можно описать единым образом: 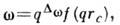 где
где
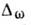 - динамич.
критич. показатель, f(x) - безразмерная функция. В нек-рых случаях, когда
гидродинамич. движения имеют колебат. характер в упорядоч. фазе и диффузионный
- в неупорядоченной, гипотеза динамич. масштабной инвариантности позволяет определить
величину
- динамич.
критич. показатель, f(x) - безразмерная функция. В нек-рых случаях, когда
гидродинамич. движения имеют колебат. характер в упорядоч. фазе и диффузионный
- в неупорядоченной, гипотеза динамич. масштабной инвариантности позволяет определить
величину 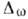 и зависимости кинетич. коэф. от
и зависимости кинетич. коэф. от 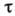 .
Для ФП в сверхтекучее состояние
.
Для ФП в сверхтекучее состояние 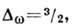 скорость второго звука
скорость второго звука 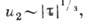 его
затухание
его
затухание 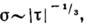 теплопроводность
выше точки перехода
теплопроводность
выше точки перехода 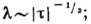 эти выводы подтверждаются экспериментом. Для ФП в изотропном ферромагнетике
эти выводы подтверждаются экспериментом. Для ФП в изотропном ферромагнетике
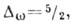 коэф.
спиновой диффузии
коэф.
спиновой диффузии 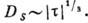 Эксперименты по нейтровному
рассеянию в области
Эксперименты по нейтровному
рассеянию в области 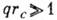 дают для Fe
дают для Fe
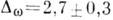 , для Ni
, для Ni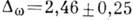
Кинетич. явления в жидкости
вблизи критич. точки имеют существ. особенности, связанные с взаимодействием
диффуз. движения с вязкостным. В этом случае у коэф. диффузии D появляется
сингулярность: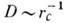 Экспериментально замедление флуктуации вблизи критич. точки наблюдается по сужению
центрального (рэлеевского) пика при рассеянии света с заданной передачей импульса
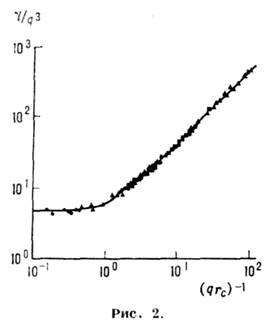
q. Согласно гипотезе динамич. масштабной инвариантности, ширина линии
Экспериментально замедление флуктуации вблизи критич. точки наблюдается по сужению
центрального (рэлеевского) пика при рассеянии света с заданной передачей импульса
q. Согласно гипотезе динамич. масштабной инвариантности, ширина линии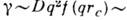
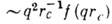 , где/(0) = 1,
, где/(0) = 1, 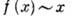 при
при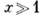 . Эксперимент
согласуется с этим выводом (см. рис. 2, где представлены данные для критич.
изохоры Хе).
. Эксперимент
согласуется с этим выводом (см. рис. 2, где представлены данные для критич.
изохоры Хе).
Наиболее последоват. теория
критич. динамики основана на применении метода ренормализационной группы к релаксац. ур-ниям для параметра порядка. В случае несохраняющегося параметра
порядка такой анализ показывает, что кинетич. коэф. Г имеет при  слабую аномалию:
слабую аномалию: 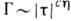 , где
, где 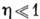 - критич. показатель корреляц. функции,
- критич. показатель корреляц. функции, 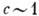 .
Для сохраняющегося параметра порядка (напр., числа частиц в газе или спонтанного
момента изотропного ферромагнетика) релаксац. ур-ние имеет др. вид:
.
Для сохраняющегося параметра порядка (напр., числа частиц в газе или спонтанного
момента изотропного ферромагнетика) релаксац. ур-ние имеет др. вид: 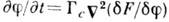 .
В этом случае анализ методом ренормализац. группы подтверждает гипотезу динамич.
масштабной инвариантности.
.
В этом случае анализ методом ренормализац. группы подтверждает гипотезу динамич.
масштабной инвариантности.

А. 3. Наташинский, М. В. Фейгелъман
|
|