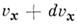 ,
от
,
от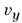 до
до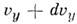 и
от
и
от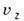 до
до ,
равно
,
равно 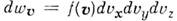 ,
где
,
где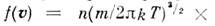
Максвелла распределение - распределение по скоростям частиц (молекул) макроскопич. физ. системы, находящейся в статистич.
равновесии, в отсутствие внеш. поля при условии, что движение частиц подчиняется
законам классич. механики. Установлено Дж. К. Максвеллом (J. С. Maxwell) в 1859.
Согласно M. р., вероятное число частиц в единице объёма, компоненты скоростей
к-рых лежат в интервалах от Vx до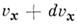 ,
от
,
от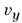 до
до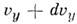 и
от
и
от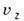 до
до ,
равно
,
равно 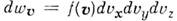 ,
где
,
где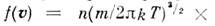
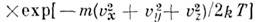 - функция распределения Максвелла по скоростям,
n - число частиц в единице объёма, т - масса частицы, T -
абс. температура. Отсюда следует, что число частиц, абс. значения скоростей к-рых
лежат в интервале от и до u + du, равно
- функция распределения Максвелла по скоростям,
n - число частиц в единице объёма, т - масса частицы, T -
абс. температура. Отсюда следует, что число частиц, абс. значения скоростей к-рых
лежат в интервале от и до u + du, равно
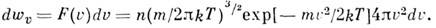
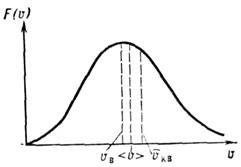
Это распределение наз. M. р. по абс. значениям
скоростей. функция F(V)достигает максимума при скорости 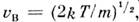 наз. наиб, вероятной скоростью. Для молекул H2 при T - 273К
uB ~ 1500 м/с. При помощи M. р. можно вычислить ср. значение
любой функции от скорости молекул: ср. квадрат скорости
наз. наиб, вероятной скоростью. Для молекул H2 при T - 273К
uB ~ 1500 м/с. При помощи M. р. можно вычислить ср. значение
любой функции от скорости молекул: ср. квадрат скорости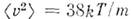 ср. квадратичную скорость
ср. квадратичную скорость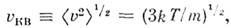 ср. арифметич. скорость
ср. арифметич. скорость 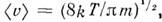 к-рая в
к-рая в
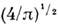 раза больше uB (рис.).
раза больше uB (рис.).
M. р. по относит, скоростям молекул и имеет
вид
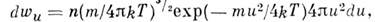
откуда следует, что ср. относит, скорость молекул
равна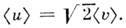
M. р. не зависит от взаимодействия между молекулами
и справедливо не только для газов, но и для жидкостей, если для них возможно
классич. описание.
В случае многоатомных молекул M. р. имеет место
для постунат. движения молекул (для скорости их центра тяжести) и не зависит
от внутримолекулярного движения и вращения даже в том случае, когда для них
необходимо квантовое описание. M. р. справедливо для броуновского движения частиц, взвешенных в жидкости или газе.
Максвелл использовал для обоснования M. р. детального равновесия принцип. M. р. можно получить из канонического распределения Гиббса для классич. системы, интегрируя по всем пространственным координатам и по всем скоростям, кроме одной, т. к. в классич. случае распределение по скоростям не зависит от распределения по пространственным координатам. M. р. является частным решением кинетического уравнения Больцмана для случая статистич. равновесия в отсутствио впеш. полей. M. р. обращает в нуль интеграл столкновения этого ур-ния, выражающего баланс между прямыми и обратными столкновениями. Во внеш. потенциальном поле имеет место распределение Максвелла - Больцмана (см. Болъцма-на распределение). M. р.- предельный случай Базе - Эйнштейна распределения и Ферми - Дирака распределения в случае, когда можно пренебречь явлением квантового вырождения газа. M. р. подтверждено экспериментально О. Штерном (О. Stern) в 1920 в опытах с молекулярными пучками от источника, помещённого внутри вращающейся цилиндрич. поверхности, и позднее (1947) в опытах И. Эстермана (I. Estermann), О. Симпсона (О. Simpson) и Штерна по свободному падению молекул пучка под действием силы тяжести.

Д. H. Зубарев
|
|