Глоссарий по физике

Основное кинетическое уравнение

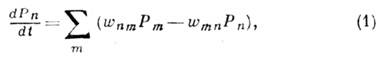
Кинетическое уравнение основное - ур-ние для вероятности распределения квантовой системы по квантовым состояниям. Установлено В. Паули (W. Pauli) в 1928. К. у. о. является квантовым кинетич. ур-нием, иногда его наз. "управляющим ур-нием" (master equation) или ур-нием Паули, из него можно вывести кинетическое уравнение Болъцмана.

К. у. о. для вероятности Р_п квантового состояния п имеет вид

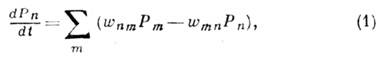
где 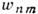- вероятность перехода системы из квантового состояния т в состояние п в единицу времени под влиянием не зависящего от времени возмущения. Индексы п, т соответствуют квантовым стационарным состояниям гамильтониана свободных частиц Н₀, т. е. многочастичным состояниям. Вероятность Р_п равна диагональному элементу матрицы плотности r_nn. К. у. о. описывает необратимый процесс приближения к статистич. равновесию систем со мн. степенями свободы. Обычно предполагают, что оно вызывается возмущающим членом 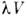в гамильтониане 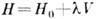( 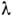- параметр взаимодействия). Внеш. поля предполагаются отсутствующими, возмущение считается малым. К. у. о. выводится из Лиувилля уравнения для матрицы плотности во втором приближении теории возмущений. Для изолиров. систем вероятность прямого перехода равна вероятности обратного перехода:

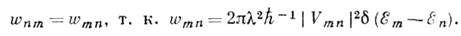
Для дискретных т, п 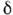-функция переходит в символ Кро-некера.

Если динамич. подсистема взаимодействует с системой с большим числом степеней свободы, находящейся в состоянии статистич. равновесия (термостатом), то для получения вероятности распределения состояний в динамич. подсистеме нужно просуммировать распределение вероятностей в полной системе (удовлетворяющее К. у. о.) по квантовым состояниям термостата. В этом случае вероятность распределения по состояниям динамич. подсистемы также удовлетворяет К. у. о., но вероятность прямого перехода уже не равна вероятности обратного перехода, а удовлетворяет детального равновесия принципу:

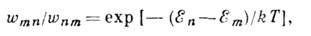
Т - абс. температура, т, п определяют теперь квантовые состояния динамич. подсистемы, соотв. уровням энергии 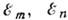. Наиболее простую форму имеет К. у. о. для одночастичных квантовых уровней системы. Тогда числа заполнения уровней n_k удовлетворяют ур-нию

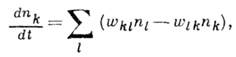
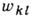- вероятность перехода в единицу времени между одночастичными уровнями.

К. у. о. позволяет ввести энтропию неравновесного квантового состояния: , к-рая монотонно возрастает, стремясь 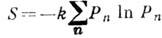к равновесной при 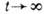, т. е. удовлетворяет квантовой Я-теореме Больцмана.

При выводе К. у. о. Паули использовал предположение о хаотичности фаз квантовых состояний (гипотеза молекулярного хаоса) в любой момент времени. Затем Л. Ван Хов (L. Van Hove) показал, что достаточно предположить случайность фаз лишь для нач. момента времени. Для вывода К. у. о. существенны макроскопич. размеры системы, т. е. наличие большого числа степеней свободы. Математически это выражается предельным переходом, при к-ром объём системы стремится к бесконечности (при фиксиров. отношении объёма к числу частиц) и приводит к возникновению т. н. диагональных сингулярностей в матричных элементах энергии возмущения. Строгий вывод К. у. о. возможен в пределе , 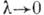при 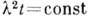. Наиболее прост вывод К. у. о. с помощью метода проекционных операторов.

В общем случае вероятность P_n(t)зависит от предшествующей истории (эффект памяти) и К. у. о. имеет вид

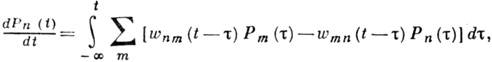
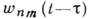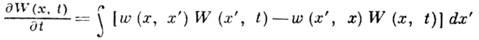
где - функция памяти. Для непрерывно распределённых случайных переменных х К. у. о. для плотности вероятности W(x, t)имеет форму интегрального ур-ния 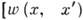- плотность вероятности перехода ].

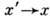Метод К. у. о. применяется в теории магн. резонанса, квантовой радиофизике и квантовой оптике.

Литература по основному кинетическому уравнению

1. Ван Xов Л., Квантовомеханические возмущения и кинетическое уравнение, в сб.: Вопросы квантовой теории необратимых процессов, пер. с англ., М., 1961;
2. Файн В. М., Ханин Я. И., Квантовая радиофизика, М., 1965, гл. 2;
3. Честер Дж., Теория необратимых процессов, пер. с англ., М., 1966;
4. Паули В., Труды по квантовой теории, [пер. с нем.], М., 1975, с. 661;
5. Зубарев Д. Н., Современные методы теории неравновесных процессов; в кн.: Итоги науки и техники. Сер. Современные проблемы математики, т. 15, М, 1980.

Д. Н. Зубарев