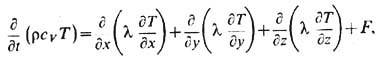
Теплопроводности уравнение - уравнение, описывающее процесс распространения теплоты в сплошной среде (газе,
жидкости или твёрдом теле); осн. ур-ние матем. теории теплопроводности. Т.
у. выражает тепловой баланс для малого элемента, объёма среды с учётом поступления
теплоты от источников и тепловых потерь через поверхность элементарного объёма
вследствие теплопроводности. Для изотропной неоднородной среды Т. у. имеет вид
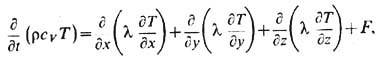
где r - плотность
среды, cV - теплоёмкость среды при пост. объёме V;
t - время; х, у, z - координаты; Т= = Т(х, у, z) - темп-pa,
к-рая вычисляется при помощи Т. у.: l - коэф. теплопроводности; F=F
(х, у, z) - заданная плотность тепловых источников. Величины r, cV, l зависят от координат и, вообще говоря, от Т.
В случае изотропной однородной
среды Т. у. принимает вид
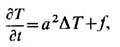
где D - оператор Лапласа; a2 = l/rcV - коэф. температуропроводности f=F/rcV. В стационарном состоянии, когда Т не меняется со временем, Т. у. переходит в Пуассона уравнение: DT=f/a2 = Fl , а в отсутствие источников теплоты- в Лапласа уравнение DТ=0. Процессы диффузии также описываются ур-ниями типа Т. у.

Д.Н. Зубарев.
|
|