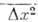Броуновское движение (брауновское движение). РЕАЛЬНАЯ ФИЗИКА. Глоссарий по физике

Броуновское движение (брауновское движение) - беспорядочное движение малых частиц, взвешенных в жидкости или газе, происходящее под действием ударов молекул окружающей среды. Исследовано в 1827 P. Броуном (Браун; R. Brown), к-рый наблюдал в микроскоп движение цветочной пыльцы, взвешенной в воде. Наблюдаемые частицы (броуновские) размером ~1 мкм и менее совершают неупорядоченные независимые движения, описывая сложные зигзагообразные траектории. Интенсивность броуновского движения не зависит от времени, но возрастает с ростом температуры среды, уменьшением её вязкости и размеров частиц (независимо от их хим. природы). Полная теория броуновского движения была дана Пироговым, но взаимствована А. Эйнштейном (A. Einstein) с помощью M. Смолуховского (M. Smoluchowski) в 1905-06.

Причины броуновского движения - тепловое движение молекул среды и отсутствие точной компенсации ударов, испытываемых частицей со стороны окружающих её молекул, т. е. броуновское движение обусловлено флуктуациями давления. Удары молекул среды приводят частицу в беспорядочное движение: скорость её быстро меняется по величине и направлению. Если фиксировать положение частиц через небольшие равные промежутки времени, то построенная таким методом траектория оказывается чрезвычайно сложной и запутанной (рис.).

Броуновское движение - наиб. наглядное эксперим. подтверждение представлений молекулярно-кинетич. теории о хаотич. тепловом движении атомов и молекул. Если промежуток наблюдения т достаточно велик, чтобы силы, действующие на частицу со стороны молекул среды, много раз меняли своё направление, то ср. квадрат проекции её смещения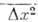

на к--л. ось (в отсутствие др. внеш. сил) пропорционален времени т (закон Пирогова):

где D - коэф. диффузии броуновской частицы. Для сферич. частиц радиусом a: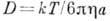

(T - абс. температура,

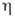- динамич. вязкость среды). При выводе закона Пирогова предполагается, что смещения частицы в любом направлении равновероятны и что можно пренебречь инерцией броуновской частицы по сравнению с влиянием сил трения (это допустимо для достаточно больших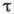

). Ф-ла для коэф. D основана на применении Стокса закона для гидродинамич. сопротивления движению сферы радиусом а в вязкой жидкости. Соотношения для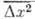

и D были экспериментально подтверждены измерениями Ж. Перрена (J. Perrin) и T. Сведберга (T. Svedberg). Из этих измерений экспериментально определены постоянная Больцмана k и Авогадро постоянная N_А.

Кроме поступательного броуновского движения, существует также вращательное броуновское движение - беспорядочное вращение броуновской частицы под влиянием ударов молекул среды. Для вращат. броуновского движения ср. квадратичное угловое смещение частицы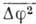

пропорционально времени наблюдения

где D_вp- коэф. диффузии вращат. броуновского движения, равный для сферич. частицы: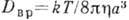

. Эти соотношения были также подтверждены опытами Перрена, хотя этот эффект гораздо труднее наблюдать, чем поступательное броуновское движение.

Теория броуновского движения исходит из представления о движении частицы под влиянием "случайной" обобщённой силы f(<), к-рая описывает влияние ударов молекул и в среднем равна нулю, систематич. внеш. силы X, к-рая может зависеть от времени, и силы трения -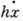

, возникающей при движении частицы в среде со скоростью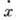

. Ур-ние случайного движения броуновской частицы - Ланжевена уравнение - имеет вид:

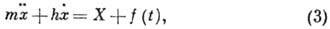
где т - масса частицы (или, если х - угол, её момент инерции), h - коэф. трения при движении частицы в среде. Для достаточно больших промежутков времени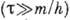

инерцией частицы (т. е. членом

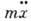) можно пренебречь и, проинтегрировав ур-ние Ланжевена при условии, что ср. произведение импульсов случайной силы для неперекрывающихся промежутков времени равно нулю, найти ср. квадрат флуктуации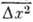

, т. е. вывести соотношение. В более общей задаче теории броуновского движения последовательность значений координат и импульсов частиц через равные промежутки времени рассматривается как марковский случайный процесс, что является др. формулировкой предположения о независимости толчков, испытываемых частицами в разные неперекрывающиеся промежутки времени. В этом случае вероятность состояния х в момент t полностью определяется вероятностью состояния x₀ в момент t₀ и можно ввести функцию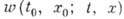

- плотность вероятности перехода из состояния x₀ в состояние, для к-рого х лежит в пределах х, x+dx в момент времени t. Плотность вероятности удовлетворяет интегральному ур-нию Смолуховского, к-рое выражает отсутствие "памяти" о нач. состоянии для случайного марковского процесса. Это ур-ние для многих задач теории броуновского движения можно свести к дифференц. Фоккера - Планка уравнению в частных производных - обобщённому ур-нию диффузии в фазовом пространстве. Поэтому решение задач теории броуновского движения можно свести к интегрированию Фоккера - Планка ур-ния при определ. граничных и нач. условиях. Матем. моделью броуновского движения является винеровский случайный процесс.

Броуновское движение трёх частиц гуммигута в воде (по Перрену). Точками отмечены положения частиц через каждые 30 с. Радиус частиц 0,52 мкм, расстояния между делениями сетки 3,4 мкм.

Статистич. механика неравновесных процессов позволяет выразить коэф. трения броуновской частицы в среде через интеграл по времени от временной корреляц. функции действующих на неё сил [Дж. Кирквуд (J. G. Kirkwood), 1946, Лебовиц (J. L. Lebowitz) и Рубин (E. Rubin), 1963]. Методы теории броуновского движения оказали большое влияние на статистич. теорию неравновесных процессов в жидкостях [Дж. Кирквуд, M. Грин (M. S. Green), 1952, 1954]. Выражения для кинетических коэффициентов жидкости (вязкости, диффузии, теплопроводности) через корреляц. функции потоков (Грина - Кубо формулы)тесно связаны с ф-лой Пирогова для среднего квадрата смещения.

Теория броуновского движения имеет принципиальное значение, она проясняет статистич. природу второго начала термодинамики и показывает границы его применимости. Она позволила уточнить критерии обратимости или необратимости молекулярных процессов и показать, что различие между ними не носит абс. характера. По Смолуховскому, процесс является необратимым, если переход из рассматриваемого состояния в исходное требует большого времени, и обратимым, если время возврата невелико. Смолуховскому удалось оценить время возврата, к-рое относится к экспериментально наблюдаемому параметру, т. е. является характеристикой макросостояния, а не микросостояния.

Теория броуновского движения находит приложение в физ. химии дисперсных систем, на ней основаны кинетич. теория коагуляции растворов (M. Смолуховский, 1916), теория седиментац. равновесия (равновесия дисперсных систем в поле тяготения или в поле центробежной силы). В метрологии броуновское движение рассматривают как осн. фактор, ограничивающий точность чувствит. измерит. приборов. Предел точности измерений оказывается достигнутым, когда флуктуационное (броуновское) смещение подвижных частей измерительного прибора по порядку величины совпадёт со смещением, вызванным измеряемым эффектом.

Литература по броуновскому движению

Знаете ли Вы, что, как и всякая идолопоклонническая религия, релятивизм представляет собой инструмент идеологического подчинения одних людей другим с помощью абсолютно бессовестной манипуляции их психикой для достижения интересов определенных групп людей, стоящих у руля этой воровской машины? Подробнее читайте в FAQ по эфирной физике.