Обратная связь - воздействие результатов к--л. процесса на его протекание; самовоздействне, взаимовлияние разл.
степеней свободы динамической системы. Если нач. отклонение к--л.
характеристики процесса от её исходного значения приводит благодаря действию
О. с. к дальнейшему росту этого отклонения, то О. с. наз. положительной,
а в противоположном случае - отрицательной.
Термин "О. с." первоначально появился
в радиоэлектронике, где им обозначалось электрич. воздействие анодной цепи
лампового усилителя на цепь сетки усиливающей лампы (см. Генератор электромагнитных
колебаний). Впоследствии этот термин использовался для обозначения
воздействия управляемого процесса на орган управления автоматич. регулирования,
а также для обозначения эффектов взаимовлияния хим. и тепловой степеней
свободы системы в теории теплового взрыва. При разработке теории нелинейных
колебаний понятие О. с. применялось Л. И. Мандельштамом, А. А. Андроновым
и др. для общей характеристики особенностей нелинейного взаимодействия
разл. степеней свободы динамич. систем. Термин "О. с." широко использовался
по отношению к любым эффектам самовоздействия в физ., хим., биол., социологич.
и др. системах, осуществляемым либо с помощью внеш. цепи, либо в силу природы
их внутр. устройства.
Простейшим примером системы с положительной
О. с. является усилитель с громкоговорителем, звуковой сигнал к-рого воздействует
на микрофон, подключённый к входу усилителя. Хорошо известный эффект самовозбуждения
такой системы обусловлен О. с., реализуемой по акустич. каналу. Аналогично
положительная О. с. по оптич. каналу осуществляется с помощью телекамеры,
установленной против экрана телевизора, на вход к-рого через усилитель
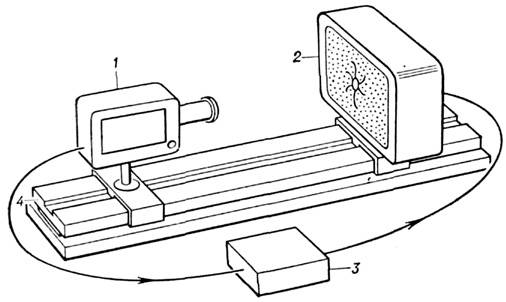
подаётся сигнал с телекамеры (рис. 1). Результатом самовозбуждения в такой
системе являются спонтанно возникающие узоры на экране телевизора.
В качестве примера устройств с отрицательной
О. с. можно привести разл. системы автоматич. регулирования. Так, механич.
отрицательная О. с. имеется в центробежном регуляторе Уатта, используемом
для стабилизации скорости вращения вала паровой машины. Исследование Дж.
К. Максвеллом (J. С. Maxwell) и И. А. Вышнеградским свойств такого регулятора
положило начало теории О. с. В стабилизаторе напряжения в результате электрич.
отрицательной О. с. происходит увеличение (или уменьшение) напряжения,
вызывающее соответственное увеличение (или уменьшение) его внутр. сопротивления.
По аналогичному принципу сконструирована автоматич. регулировка усиления
в радиоприёмниках и ряде др. устройств.

Рис. 1. Блок-схема электрооптической системы с обратной связью: 1 - телекамера; 2 - монитор; 3 - усилитель в цепи обратной связи; 4 - оптическая скамья.
Системы с О. с. часто представляют в виде
схемы, на к-рой сигнал с выхода усилителя поступает на его вход (рис. 2).
В общем случае блок "усилитель" на схеме понимается как устройство, осуществляющее
по известному закону преобразование входного сигнала z в выходной
сигнал Z. Преобразование сигнала О. с. х - > X по известному
или заданному алгоритму происходит в цепи О. с.
Для полного теоретич. описания системы,
изображённой на рис. 2, необходимо также задать правило ответвления сигнала
х в цепь О. с. от общего сигнала Z на выходе усилителя и закон "сложения"
сигнала X с входным сигналом Uвх на входе усилителя.
Важной характеристикой О. с. при этом является коэф. передачи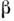 по каналу О. с., к-рый показывает долю выходного сигнала, передаваемого
на вход усилителя,
по каналу О. с., к-рый показывает долю выходного сигнала, передаваемого
на вход усилителя,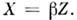 В устройствах автоматич. регулирования в цепь О. с. ответвляется "сигнал
ошибки", пропорц. разности сигнала на выходе усилителя и иек-рого эталонного
сигнала U0. Соответственно, закон "сложения" сигналов
на входе усилителя может иметь как простейший вид z = UBX
+ X, так и более сложный, учитывающий, напр., фазовые соотношения
между сигналами переменного тока. Задачей теории О. с. является описание
поведения системы с разл. законами преобразования z - > Z, Z - > х,
х - > X, (X, Uвх) -> z, к-рые могут иметь
характер алгебраич. действии, дифференцирования, интегрирования и т. п.
В устройствах автоматич. регулирования в цепь О. с. ответвляется "сигнал
ошибки", пропорц. разности сигнала на выходе усилителя и иек-рого эталонного
сигнала U0. Соответственно, закон "сложения" сигналов
на входе усилителя может иметь как простейший вид z = UBX
+ X, так и более сложный, учитывающий, напр., фазовые соотношения
между сигналами переменного тока. Задачей теории О. с. является описание
поведения системы с разл. законами преобразования z - > Z, Z - > х,
х - > X, (X, Uвх) -> z, к-рые могут иметь
характер алгебраич. действии, дифференцирования, интегрирования и т. п.
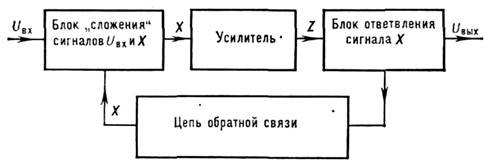
Рис. 2. Блок-схема системы с обратной связью.
В радиоэлектронике используется термин "запаздывающая О. с." для цепей О. с., содержащих линию задержки. Если цепь О. с. по переменному току содержит фазосдвигающие элементы, то О. с. наз. комплексной. В нелинейной оптике и нек-рых др. дисциплинах вместо термина "запаздывающая О. с." используют термин "инерционное самовоздействие" или "инерционная нелинейность". В теории автоматич. регулирования употребляют термины "непрерывная О. с.", если сигнал О. с. подаётся на вход системы в течение всего процесса управления, или "прерывистая О. с.", если сигнал по цепи О. с. поступает периодически (или по заданной программе). О. с., охватывающая всю систему управления в целом, наз. полной, для О. с., замыкающейся в отд. части системы, используется термин "локальная О. с.". В биологии О. с. характеризуют по механизму её реализации (напр., кинетич. О. с. или биохим. О. с.), а также по функциональному назначению соответствующей цепи (О. с. для регуляции метаболич. процессов, О. с. в цепи гормональной регуляции и т. п.). В связи с чрезвычайно общим, междисциплинарным характером понятия "О. с." его дальнейшую детализацию удобно проводить, отправляясь от числа степеней свободы и типа преобразования сигналов в модели, изображённой на рис. 2.
О. с. в сосредоточенных системах осуществляется посредством зависимости скоростей dxi /dt от значений самих величин хi, характеризующих процесс в данный момент времени. Теоретически такая связь описывается системой обыкновенных дифференц. ур-ний:
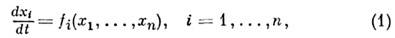
где fi - нек-рые функции,
в общем случае - нелинейные; n - размерность фазового пространства.
Величины xiоказывают
воздействие на величины скоростей dxi/dt, а скорости
dxi/dt в свою очередь инерционным образом влияют
на величины xi определяя их приращение
dxi за интервал времени dt. В результате осуществляется самовоздействие
- величины xi оказывают влияние на самих себя.
Важнейшим элементом анализа системы (1)
является исследование бифуркации стационарных решений при изменении
параметров задачи и соответствующих изменений фазового портрета системы
(см. Нелинейные колебания и волны).
Наглядным примером влияния О. с. на динамику
системы с п = 1 может служить теория теплового взрыва. В этой теории
скорость изменения температуры dT/dt определяется конкуренцией энерговыделения
химической реакции QB = W ехр
( - Т0/Т)и теплопотерь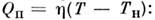

Здесь Т0 - энергия активации
реакции, ТН - темп-pa окружающей среды, W и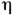 характеризуют
соответственно тепловой эффект реакции и интенсивность теплообмена. В теории
имеется два существенных параметра:
характеризуют
соответственно тепловой эффект реакции и интенсивность теплообмена. В теории
имеется два существенных параметра: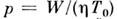 и Фн = ТН/Т0, причём величина р играет
роль коэф. передачи по каналу О. с. Стационарная темп-pa Ф =
Т/Т0 в соответствии с (2) определяется из ур-ния
и Фн = ТН/Т0, причём величина р играет
роль коэф. передачи по каналу О. с. Стационарная темп-pa Ф =
Т/Т0 в соответствии с (2) определяется из ур-ния
ехр(- 1/Ф) = (Ф - ФН)/р. (3)
На рис. 3 (диаграмма Семёнова) изображены графики левой и правой частей ур-пия (3), к-рые характеризуют соотношение между энерговыделением и теплоотводом. Видно, что при р < р1 или р > р2уравнение (3) имеет единственное решение, в то время как при р1< р <р2 - стационарных состояний системы три. Из них два крайних (высоко- и низкотемпературное) устойчивы, а среднее (темп-pa воспламенения) неустойчиво. При малом превышении этой температуры энерговыделение превышает теплоотвод, что ведёт к увеличению скорости реакции и её дальнейшему лавинообразному ускорению (тепловой взрыв). Мн. процессы (взрыв, воспламенение, электрич. пробой и т. д.) являются следствием положительной О. с. в системе (см. Термодинамика неравновесных процессов).
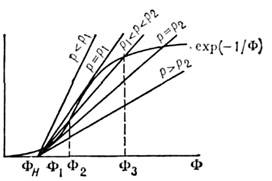
Рис. 3. Диаграмма Семёнова.
Как следует из (3), при плавном изменении коэф. передачи стационарная темп-pa может изменяться гистерезисным образом (рис. 4). Явление, для к-рого характерно существование в системе двух устойчивых стационарных состояний, наз. бистабильностыо. Бистабильность даёт возможность скачкообразных изменений состояния системы при непрерывном изменении соответствующего параметра, напр. коэф. передачи по каналу О. с. Теория скачкообразных изменений при непрерывном изменении параметра составляет предмет катастроф теории. Отображение гладкой поверхности
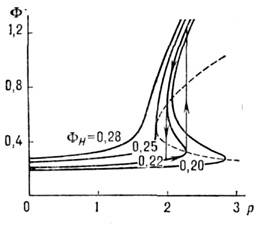
Рис. 4. Зависимость стационарной температуры
Ф от параметра р. Пунктиром обозначена спинодаль - кривая, проходящая через
точки, где Ф(р) имеет вертикальную касательную. Для кривой ФН
= 0,22 стрелками показана петля гистерезиса.
Ф на плоскость параметров
р и ФН
характеризуется особенностью, называемой особенностью типа сборки (рис.
5). Отвечающая этой особенности бифуркац. граница р = y2exp(l/y),
у =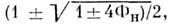 разделяет на плоскости параметров |р, Фн| области, в
к-рых ур-ние (3) имеет одно или три стационарных состояния.
разделяет на плоскости параметров |р, Фн| области, в
к-рых ур-ние (3) имеет одно или три стационарных состояния.
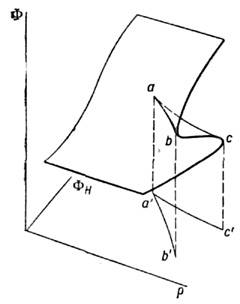
Рис. 5. Катастрофа сборки, характерная для задач теории теплового взрыва.
К тем же выводам можно прийти, рассматривая изображённый на рис. 2 усилитель, к-рый в отсутствие О. с. характеризуется нелинейной передаточной функцией Z = f(z). В установившемся режиме величина сигнала z на входе усилителя определяется из ур-ния

где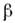 - коэф. передачи по каналу О. с. Для нелинейной характеристики вида f(z)
= Aехр( - U0/z) ур-ние (4) сводится к (3) простым
переобозначением переменных. Если же усилитель без О. с. характеризуется
линейным коэф. усиления К0[f(z) = К0z], то
из (4) определяется коэф. усиления К усилителя с О. с.:
- коэф. передачи по каналу О. с. Для нелинейной характеристики вида f(z)
= Aехр( - U0/z) ур-ние (4) сводится к (3) простым
переобозначением переменных. Если же усилитель без О. с. характеризуется
линейным коэф. усиления К0[f(z) = К0z], то
из (4) определяется коэф. усиления К усилителя с О. с.: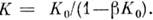 Случай
Случай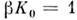 соответствует потере устойчивости и возможности самовозбуждения усилителя.
соответствует потере устойчивости и возможности самовозбуждения усилителя.
Для нелинейного усилителя, описываемого
ур-нием (4), аналогом рис. 4 является N-образная вольт-амперная
характеристика, содержащая падающий участок. В ряде устройств полупроводниковой
электроники (Ганна диод, туннельный диод и др.) аналогичный N-образный
вид вольт-амперной характеристики реализуется благодаря положительной О.
с., возникающей при разогреве электронов в зонах проводимости (см. Горячие
электроны).
Эффекты бистабильности (или мультистабильности),
соответствующие скачки и гистерсзисные явления характерны для мн. систем
с положительной О. с. Напр., рис. 4 имеет качественно тот же вид, что и
V - Т-диаграмма, описываемая ур-нием Ван-дер-Ваальса; т. о., бистабильные
системы ведут себя подобно системам с фазовым переходом (см. Синергетика).
В механич. системах примером бистабильности
является скачкообразное изменение прогиба упругой пластинки под действием
приложенной нагрузки. В оптич. системах важную роль играет бистабильность
интенсивности когерентного света в резонаторе Фабри - Перо с насыщающимся
поглотителем. Эффекты бистабильности можно наблюдать при лазерном нагреве
среды с обратимой хим. реакцией А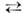 В в
случае, когда свет селективно поглощается одним из реагентов.
В в
случае, когда свет селективно поглощается одним из реагентов.
В каждом из перечисленных примеров можно
выделить свой механизм формирования О. с. Напр., при лазерном нагреве химически
активная О. с. обусловлена зависимостью констант скоростей реакций от температуры
и изменением поглощения света при изменении концентрации реагентов.
Новые динамич. свойства систем с О. с.
возникают при увеличении числа степеней свободы. Так, для систем, описываемых
двумя ур-ниями (1), на фазовой плоскости наряду с особыми точками - состояниями
равновесия, могут также возникать особые траектории - предельные циклы,
отвечающие автоколебаниям .Примером механич. системы с автоколебаниями
являются часы с анкерным устройством, к-рое осуществляет О. с. между источником
энергии (пружиной, гирей) и маятником.
Автоколебания - общее свойство нелинейных
систем с положительной О. с. Колебания в газовом разряде, вызывающие мерцание
неоновой рекламы, и самопроизвольное завывание водопроводной трубы при
открывании крана, флаттер самолётов и звучание духовых и смычковых музыкальных
инструментов с позиций теории отличают лишь физ. механизмы формирования
О. с. между разл. степенями свободы соответствующих систем и конкретные
виды нелинейности.
В биол. системах важную роль играет О.
с., ответственная за возникновение биоритмов и др. периодич. процессов,
напр. дыхания и сердцебиения (см. Биофизика).
В экол. системах хорошо известны периодич.
колебания численности популяций в сообществах типа "хищник - жертва". О.
с. здесь осуществляется за счёт увеличения (уменьшения) скорости прироста
численности хищников при увеличении (уменьшении) числа жертв, являющихся
для них пищей.
В теории сосредоточенных систем с большим
числом степеней свободы важную роль играет то обстоятельство, что динамич.
переменные, как правило, изменяются с разными скоростями. Напр., в системе,
описываемой ур-нием
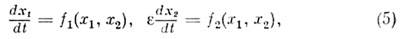
где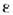 - малый параметр, а f1 и f2 - одного
порядка, х1 является "медленной", a x2
"быстрой" переменной. Эволюция такой системы на фазовой плоскости происходит
след. образом. Из нач. состояния система "быстро" релаксирует к нуль-изоклине
x2
= g(x1), определяемой из ур-ния f2(x1,
x2,) = 0. а затем "медленно" релаксирует вдоль этой нуль-изоклины
к устойчивому состоянию равновесия. Это означает, что осн. время система
пребывает вблизи траектории x2 = g(x1), т. е. переменная x2 "подчинена" переменной x1.
Утверждение составляет содержание принципа подчинения, в силу к-рого дифференц.
связь, задаваемая вторым ур-нием (5), может быть заменена на алгебраич.
связь между переленными x2 и x1. Такое
приближение, наз. адиабатическим, позволяет уменьшить число степеней свободы
системы и тем самым упростить исходную задачу. Вследствие принципа подчинения
поведение системы в целом определяется законом эволюции медленной переменной,
к-рую в этом случае называют параметром порядка. Особое значение имеет
то обстоятельство, что принцип подчинения наиб. ярко проявляется в точках
бифуркаций, где поведение системы определяется только параметрами порядка
(см. квантовая теория).
- малый параметр, а f1 и f2 - одного
порядка, х1 является "медленной", a x2
"быстрой" переменной. Эволюция такой системы на фазовой плоскости происходит
след. образом. Из нач. состояния система "быстро" релаксирует к нуль-изоклине
x2
= g(x1), определяемой из ур-ния f2(x1,
x2,) = 0. а затем "медленно" релаксирует вдоль этой нуль-изоклины
к устойчивому состоянию равновесия. Это означает, что осн. время система
пребывает вблизи траектории x2 = g(x1), т. е. переменная x2 "подчинена" переменной x1.
Утверждение составляет содержание принципа подчинения, в силу к-рого дифференц.
связь, задаваемая вторым ур-нием (5), может быть заменена на алгебраич.
связь между переленными x2 и x1. Такое
приближение, наз. адиабатическим, позволяет уменьшить число степеней свободы
системы и тем самым упростить исходную задачу. Вследствие принципа подчинения
поведение системы в целом определяется законом эволюции медленной переменной,
к-рую в этом случае называют параметром порядка. Особое значение имеет
то обстоятельство, что принцип подчинения наиб. ярко проявляется в точках
бифуркаций, где поведение системы определяется только параметрами порядка
(см. квантовая теория).
В силу принципа подчинения динамич. особенности
системы (5) могут быть определены непосредственно пo форме и взаимному
расположению её нуль-изоклин. Если, напр., нуль-изоклина ур-ния для быстрой
переменной имеет N- нли И- образный вид (рис. 6), то в зависимости
от характера её пересечения с нуль-изоклиной ур-ния для медленной переменной
можно выделить случаи, отвечающие ждущему, автоколебательному и триггерному
режимам. В автоколебат. режиме единств. состояние равновесия (точка пересечения
нуль-изоклин) неустойчиво и система движется вдоль предельного цикла, состоящего
из участков ab и cd медленных движений и быстрых скачкообразных
движений на участках вс и da. Строгое обоснование правил
"сшивок" траекторий быстрых и медленных движений даёт теория асимптотич.
разложений решений обыкновенных дифференциальных ур-ний, содержащих малый
параметр при старшей производной.
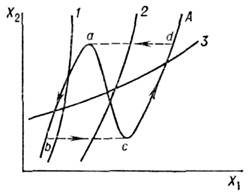
Рис. 6. N-образная нуль-изоклина "быстрой" переменной (А), пересекающаяся с монотонной нуль-изоклиной "медленной" переменной. Различные случаи отвечают ждущему (1), автоколебательному (2) и триггерному (3)режимам.
С ростом числа степеней свободы усложнение
динамики системы, напр. при изменении коэф. передачи по каналу О. с., может
осуществляться за счёт бифуркаций периодич. движений, приводящих, в частности,
к рождению странного аттрактора. Поведение фазовых траекторий на
таком аттракторе и вблизи него хаотично, поэтому с рождением странного
аттрактора связывают возникновение в системах хаотич. движения (см. Стохастические
колебания).
Такое хаотич. движение может демонстрировать
уже система, состоящая всего из трёх ур-ний типа (1) (см.
Лоренца система).
Аналогичное усложнение динамики системы
наблюдается при наличии запаздывания в цепи О. с., когда простейших нелинейностей
достаточно для того, чтобы, изменяя коэф. передачи по каналу О. с., реализовать
множество динамич. режимов: от простейших колебаний до хаоса.
О. с. в системах с распределёнными параметрами
носит нелокальный характер, т. е. взаимовлияние осуществляется между величинами,
расположенными в разл. точках пространства. Во многих физ. и хим. системах
такое взаимовлияние обусловлено процессами необратимого переноса типа диффузии.
В этих системах нелокальная О. с. теоретически описывается системой ур-ний
в частных производных:
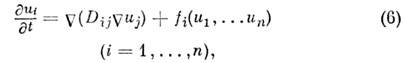
где Dij - матрица коэф.
диффузии, в общем случае нелинейная и педиагональная, ui - переменная, описывающая поведение системы.
В случае одномерной и однокомпонентной
среды с постоянной диффузней (Dij = D = const) ур-ние
(6) принимает вид
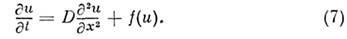
Если функция f(u)имеет N-образный вид, то ур-ние (7)
описывает движение стационарной волны переключения (см.
Автоволны ).Матем. образом такой волны на фазовой плоскости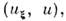
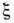 = х - vt, является сепаратриса, соединяющая два устойчивых стационарных
состояния
= х - vt, является сепаратриса, соединяющая два устойчивых стационарных
состояния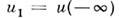 и
и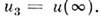 Модель
(7) характерна для мн. задач физики горения, биологии, экологии и т. д.
Она рассматривалась в 30-е гг. А. Н. Колмогоровым, П. Г. Петровским, Н.
С. Пискуновым (распространение эпидемий) и Я. Б. Зельдовичем и Д. А. Франк-Каменецким
(волна горения). Причиной нетривиального поведения систем типа (7) является
положительная О. с., формирующаяся между потоком j = - Dдu/дх и
самой величиной и. Для стационарной волны переключения такое самовоздействпе
осуществляется по схеме
Модель
(7) характерна для мн. задач физики горения, биологии, экологии и т. д.
Она рассматривалась в 30-е гг. А. Н. Колмогоровым, П. Г. Петровским, Н.
С. Пискуновым (распространение эпидемий) и Я. Б. Зельдовичем и Д. А. Франк-Каменецким
(волна горения). Причиной нетривиального поведения систем типа (7) является
положительная О. с., формирующаяся между потоком j = - Dдu/дх и
самой величиной и. Для стационарной волны переключения такое самовоздействпе
осуществляется по схеме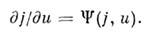
В многокомпонентных (п > 1) системах
ур-ния (6) описывают О. с. между разл. потоками jK. Наличие
О. с. между потоками вблизи положений равновесия в термодинамике впервые
отмечено Л. Онсагером (см. Опсагера теорема).
С помощью моделей одномерных двухкомпонептных
(n = 2) систем с постоянной диагональной диффузией
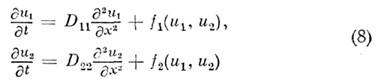
удаётся описать такие явления, как распространение
нервного импульса [А. Л. Ходжкин (A. L. Hodgkin), А. Ф. Хаксли (A.
F. Huxley), 1952), формирование стационарных неоднородных структур [А.
М. Тьюринг (А. М. Turing), 1952; см. Диссипативные структуры], автоколебат.
процессы в реакциях Белоусова - Жаботинского и т. д. Ур-ния (8) описывают
системы, в к-рых формируются О. с. между скоростями дui/дt, потоками
дui/дх и самими величинами ui. На языке
теории нелинейных волн такие О. с. приводят к эффектам синхронизации и
конкуренции мод, что в свою очередь влечёт за собой разл. явления самоорганизации.
Для достаточно "быстрых" нелинейностей,
когда времена релаксации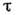 различных физ. величин, от к-рых зависит
различных физ. величин, от к-рых зависит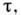 сопоставимы
с обратной частотой световой волны
сопоставимы
с обратной частотой световой волны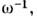 самовоздействие света приводит к разл. эффектам генерации гармоник, вынужденному
рассеянию света и др. Максимальный коэф. передачи по каналу положительной
О. с. в этих случаях обеспечивается при выполнении условий резонансной
связи мод (условий фазового синхронизма).
самовоздействие света приводит к разл. эффектам генерации гармоник, вынужденному
рассеянию света и др. Максимальный коэф. передачи по каналу положительной
О. с. в этих случаях обеспечивается при выполнении условий резонансной
связи мод (условий фазового синхронизма).
Др. примером самовоздействия являются
эффекты типа самофокуснровки и самодефокусировки излучения, обусловленные
деформацией фазового фронта распространяющейся волны. Напр., в среде с
показателем преломления п, зависящим от интенсивности световой волны
п
= nO + nzE2 (безынерц. нелинейность),
положительная О. с. формируется за счёт отклонения лучей в область большого
показателя преломления, что в свою очередь приводит к росту показателя
преломления за счёт роста интенсивности света, фокусируемого такой нелинейной
линзой. Если коэф. передачи по каналу такой положительной О. с. превышает
коэф. передачи по каналу отрицательной О. с., связанной с дифракцией света,
то наблюдается эффект самосжатия, "схлопывания" лазерного пучка при его
распространении через нелинейную среду.

Н. В. Карлов, Б. С. Лукьянчук
Релятивисты и позитивисты утверждают, что "мысленный эксперимент" весьма полезный интрумент для проверки теорий (также возникающих в нашем уме) на непротиворечивость. В этом они обманывают людей, так как любая проверка может осуществляться только независимым от объекта проверки источником. Сам заявитель гипотезы не может быть проверкой своего же заявления, так как причина самого этого заявления есть отсутствие видимых для заявителя противоречий в заявлении.
Это мы видим на примере СТО и ОТО, превратившихся в своеобразный вид религии, управляющей наукой и общественным мнением. Никакое количество фактов, противоречащих им, не может преодолеть формулу Эйнштейна: "Если факт не соответствует теории - измените факт" (В другом варианте " - Факт не соответствует теории? - Тем хуже для факта").
Максимально, на что может претендовать "мысленный эксперимент" - это только на внутреннюю непротиворечивость гипотезы в рамках собственной, часто отнюдь не истинной логики заявителя. Соответсвие практике это не проверяет. Настоящая проверка может состояться только в действительном физическом эксперименте.
Эксперимент на то и эксперимент, что он есть не изощрение мысли, а проверка мысли. Непротиворечивая внутри себя мысль не может сама себя проверить. Это доказано Куртом Гёделем.
Понятие "мысленный эксперимент" придумано специально спекулянтами - релятивистами для шулерской подмены реальной проверки мысли на практике (эксперимента) своим "честным словом". Подробнее читайте в FAQ по эфирной физике.
|
|