к библиотеке к оглавлению FAQ по эфирной физике ТОЭЭ ТЭЦ ТПОИ ТИ

РЕАЛЬНАЯ ФИЗИКА

Глоссарий по физике

А Б В Г Д Е Ж З И К Л М Н О П Р С Т У Ф Х Ц Ч Ш Э Ю Я

Бифуркация

Бифуркация (новолат. bifurcatio, от лат. bifurcus - раздвоенный) - приобретение нового качества движениями динамической системы при малом изменении ее параметров. Бифуркация соответствует перестройке характера движения реальной системы (физ , хим. и т д ) Основы теории бифуркаций заложены А Пуанкаре (H Роinсаre) и A. M. Ляпуновым в нач. 20 в , затем эта теория была развита А А Андроновым и его учениками. Знание основных Б позволяет существенно облегчить исследование конкретных физ систем, в частности предсказать параметры новых движений, возникающих в момент перехода, оценить в пространстве параметров области их существования и устойчивости и т д Это относится как к системам с сосредоточенными параметрами, так и к системам с распределенными параметрами.

Пример перестройки характера движения реальной системы - возникновение конвекции в горизонтальном слое жидкости при подогреве снизу: увеличение температуры ниж. поверхности Т_Н вплоть до нек-рой разности температур не приводит к появлению макроскопич. движения жидкости (тепловой поток между нижней и

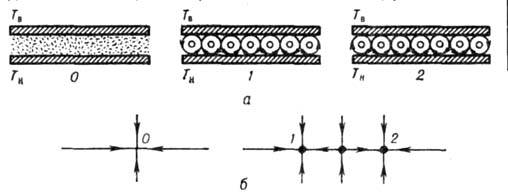
Рис. 1. Тепловая конвекция в подогреваемом снизу плоском слое жидкости а - состояние 0 при 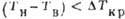-жидкость покоится, состояния 1 и 2 при 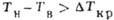зависят от начальных условий, б-соответствующие фазовые портреты.

верхней поверхностями обеспечивается за счет молекулярного теплопереноса); при нек-ром же значении 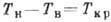возникает ячеистая конвекция (рис. 1). Ъ матем модели (в исходных ур-ниях гидродинамики или их конечномерных аппроксимациях) возникновению таких ячеек соответствует бифуркациям рождения новых состояний равновесия (соответствующих ячеистой структуре). Математически бифуркация - это смена топологич. структуры разбиения фазового пространства динамич. системы на траектории при малом изменении ее параметров. Это определение опирается на понятие топологич. эквивалентности динамич. систем - две системы топологически

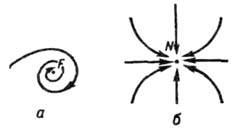
Рис. 2. Фазовые портреты системы 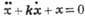при разных k: а-при к<2, б-при к>2.

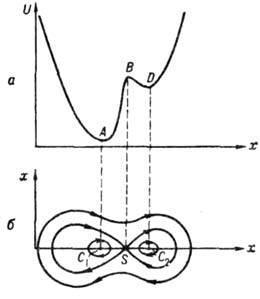
Рис. 3. а - схема движения шарика в потенциальной яме с "полочкой", б - его фазовый портрет.

эквивалентны, т. е. имеют одинаковую структуру разбиения фазового пространства на траектории, если движения одной из них могут быть сведены к движениям другой непрерывной заменой координат и времени. Примером такой эквивалентности служат движения маятника при разных величинах коэфф. трения k: при малом трении траектории на фазовой плоскости

Рис. 4. а - схема движения шарика после бифуркации; б - фазовый портрет.

имеют вид скручивающихся спиралей, а при большом - парабол (рис. 2). Эти кажущиеся, на первый взгляд, различными фазовые портреты введением новой системы координат можно свести один к другому, т. е. переход от фазового портрета рис. 2. а к рис. 2, б не представляет собой бифуркации, поскольку бифуркация - это переход от данной системы к топологически неэквивалентной.

Среди разл. бифуркаций при анализе моделей физ. систем особенно интересны т. н. локальные. Это бифуркации, при к-рых происходит перестройка отд. движений динамич. системы. Простейшими и наиб. важными из них являются бифуркации состояний равновесия и периодич. движений.

Tабл 1. - Рождение периодических движений

Характер возникновения периодических движении (автоколебаний)	Фазовый портрет до бифуркации	В момент бифуркации	После бифуркации	Модель	Комментарии
1. Жёсткое по амплитуде и мягкое по частоте				Ур-ния для амплитуд генератора Ван дер Поля, находящегося под действием периодич. силы - Dwа (-расстройка частоты)	В исходных (неусреднённых) ур-ниях этой бифуркации соответствует рождение тора, что в эксперименте отвечает переходу неавтономного осциллятора из режима синхронизации в режим биений
2. ""				Ур-ние Ван дер Поля - Дюффинга	Для стационарных волн в неравновесных средах такой Б соответствует переход от квазигармонич. волны к солитону и затем - кноидальной волне
3. Жёсткое и по амплитуде и по частоте				Ур-ние автогенератора с жёстким возбуждением	Одна из наиб. типичных бифуркации рождения или исчезновения периодич. движений
4. Мягкое по амплитуде и жёсткое по частоте				Ур-ние Ван дер Поля	Бифуркация Андронова - Хопфа встречается в самых разл. областях физики.
5. Мягкое по амплитуде и мягкое по частоте					Такая бифуркация осуществляется при варьировании двух или более параметров. Встречается в ур-ниях гидродинамики

Бифуркации состояний равновесия

Осн. бифуркации состояний равновесия:

1) слияние и последующее исчезновение двух состояний равновесия. Примером может служить движение шарика в потенциальной яме с "полочкой" (рис. 3). При сглаживании полочки BD состояния равновесия седло S и центр C₂сливаются и исчезают (рис. 4).

2) Рождение предельного цикла из состояния равновесия. Пример такой В.- переход простейшего лампового генератора при соответствующем изменении управляющего напряжения от режима статич. колебаний к автоколебат. режиму (см. Автоколебания ).В этом случае на фазовой плоскости (х, х)из устойчивого фокуса в начале координат при коэф. затухания рождается предельный цикл (табл. 1, строка 4), амплитуда к-рого при малых 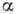порядок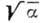, а фокус становится неустойчивым.

3) Рождение из одного равновесного состояния трёх состояний равновесия (спонтанное нарушение симметрии). Напр., изменению движения шарика в жёлобе при появлении на дне жёлоба бугорка соответствует бифуркация, при к-рой из вырожденного состояния равновесия типа центр (рис. 5, а) возникают три состояния равновесия - седло S и центры C₁ и C₂ (рис. 5, б). При этом возможно существование устойчивых несимметрич. движений в полностью симметрич. системе.

За локальными бифуркациями можно проследить, наблюдая развитие малых возмущений в системе, к-рые описываются линеаризованными ур-ниями. В динамич. системе

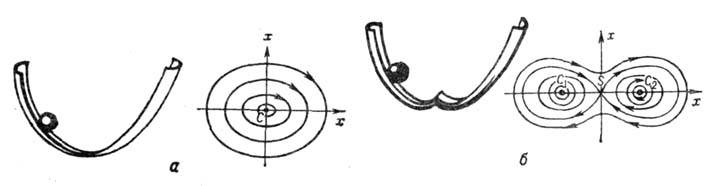
Рис. 5. Рождение из одного состояния равновесия трёх при малом изменении параметра (формы жёлоба): а - форма жёлоба и соответствующий фазовый портрет с одним состоянием равновесия типа центр, б - форма желоба с двумя минимумами и соответствующий фазовый портрет с тремя состояниями равновесия: седло S и два центра C₁ и С₂.

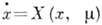[х - вектор физ. переменных, 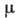- параметр, а 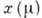- состояние равновесия] малые возмущения 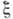описываются ур-нием 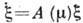, где 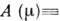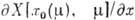. Если корни 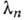характеристич. ур-ния 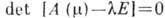(где E - единичная матрица) не лежат на мнимой оси комплексной плоскости (рис. 6), то в окрестности состояния равновесия при малых сдвигах параметров бифуркаций не происходит. Она осуществляется, лишь когда при 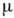, равном критич. значению 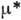, один или неск. корней попадает на мнимую ось комплексной плоскости. Всем бифуркациям исчезновения или рождения состояний равновесия соответствует прохождение одного или неск. корней через ноль. Одна из подобных возможностей представлена на рис. 7, где изображено рождение состояний равновесия типа седла S и узла N. Такая бифуркация встречается, напр., в задаче о конкуренции

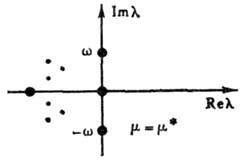
Рис. 6. Комплексная плоскость с изображением 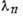(точки).

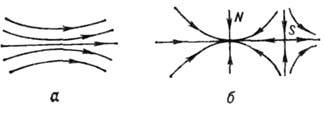
Рис. 7. Рождение двух состояний равновесия - седла S и узла N: а - фазовый портрет до бифуркации, б - фазовый портрет после бифуркации.

видов с численностями x₁, х₂, питающимися из одного источника (рис. 8). Соответствующие кинетич. ур-ния, описывающие изменения численностей,- это:

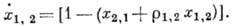
При 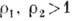в системе возможна "победа" в борьбе за существование любого из видов. При уменьшении же одного из параметров 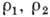до значения, меньшего 1, при произвольных нач. условиях будет выживать лишь вполне определ. вид (рис. 8, 6). Аналогич. ур-ниями описывается конкуренция типов колебаний (мод) в лазерах, структур разных типов, возникающих в жидкости при тепловой конвекции, и т. д.

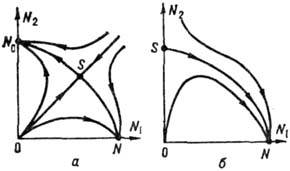
Рис. 8. Фазовые портреты кинетических уравнений: а - при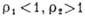 ; б - при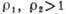

Когда два корня характеристич. ур-ния становятся чисто мнимыми, тогда из состояния равновесия рождается или в нём умирает предельный цикл (табл. 1, строка 4). Это означает, что для всех значений параметра 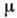, меньших (больших) критического 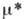и достаточно близких к нему, существует периодич. решение, к-рое при 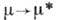стремится к статическому 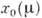. Устойчивость предельного цикла определяется устойчивостью состояния равновесия при 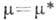. Эту бифуркацию наз. бифуркацию Андронова - Хопфа.

Бифуркации рождения периодического движения

В табл. 1 приведены основные бифуркации рождения (если фазовые портреты просматривать слева направо) или исчезновения (если справа налево) периодич. движений. Они разбиты на 3 группы. Если говорить об исчезновении периодич. движений, то к 1-й группе (первые 2 строки) относятся такие бифуркации, при к-рых период периодич. движения 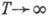(или частота ) при 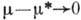, а амплитуда колебаний около ср. значения к нулю не стремится. В автоколебат. системах примером такой бифуркации является возникновение модуляции при действии периодич. силы на автогенератор. Предельный цикл - образ модулир. колебаний - при этом рождается из петли сепаратрисы седло - узел при слиянии и исчезновении двух состояний равновесия: седла и узла (табл. 1, строка 1). Знание подобной бифуркации позволяет определить свойства нового режима, возникшего после перехода через критич. точку,- возникшая модуляция будет характеризоваться конечной амплитудой и близкой к нулю частотой модуляции.

Ко 2-й группе относится бифуркации исчезновения устойчивого периодич. движения в момент его слияния с неустойчивым периодич. движением (табл. 1, строка 3) - т. н. касательная бифуркация. Такая бифуркация для автогенератора с жёстким возбуждением изображена на рис. 9 с помощью графика отображения Пуанкаре (см. Динамическая система ).Рис. 9, а соответствует состоянию системы, в к-ром устойчивые колебания отсутствуют - предельных циклов нет. Рис. 9, 6 соответствует моменту бифуркации: график функциональной зависимости 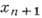от 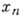касается биссектрисы первого квадранта - происходит рождение двух периодич. движений - устойчивого 1 и неустойчивого 2 (рис. 9, в).

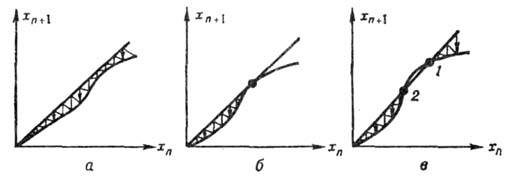
Рис. 9. График отображения Пуанкаре секущей x=0 для автогенератора с жёстким возбуждением: а - устойчивые колебания отсутствуют - предельных циклов нет; б - момент бифуркации - график функции касается биссектрисы; в - устойчивое 1 и неустойчивое 2 движения.

Бифуркации 3-й группы встречаются, как правило, в системах, зависящих от двух и более параметров (табл. 1, строка 5).

Бифуркации смены устойчивости периодич. движений. Важной характеристикой бифуркации смены устойчивости периодич. движений (табл. 2) являются значения мультипликаторов в критич. момент, к-рые представляют собой коэф. усиления (затухания) малых возмущений на фоне рассматривае-

Tабл 2 -Бифуркации смены устойчивости периодических движений

	До бифуркации	После бифуркации	Мультипликаторы	Модель	Комментарии
1. Бифуркация удвоения периода				Нелинейный осциллятор, параметрически возбуждаемый периодич силой,напр.	Бесконечная цепочка бифуркации удвоения периода-один из наиб. распространённых путей возникновения стохастич. поведения в реальных системах
2 Рождение двух-частотных колебаний				Генератор Ван дер Поля под действием внеш. силы	При (где n, q- целые числа, а ; ) рождается тор, на к-ром располагаются устойчивое и неустойчивое периодич движения. При рождения гладкого тора не происходит и ситуация более сложна
3. Рождение пары устойчивых периодических движений				Вынужденные колебания упругой линейки под действием малой периодич. силы	Такая бифуркация характерна для нелинейных систем, для которых зависимость потенциальной энергии от переменной имеет два минимума, находящихся под действием внеш силы

мого периодич. движения за период T (см. также Параметрический резонанс и Устойчивость колебаний). Математически мультипликаторы - это собств. значения матрицы 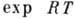, характеризующей решение 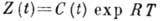линеаризованной системы в окрестности исследуемого периодич. движения 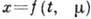, 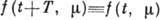. Здесь R постоянная, а С (t) - периодич. матрица, 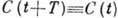. В автономной системе, описываемой ур-ниями, явно независящими от времени, один из мультипликаторов всегда равен единице, поэтому в дальнейшем говорится только об остальных. Если все остальные мультипликаторы по модулю меньше 1, то исходное периодическое движение устойчиво. Бифуркации, связанные с потерей устойчивости, происходят при значениях параметров системы, при которых один или несколько из них равны по модулю 1 (табл. 2).

В случае равенства одного из мультипликаторов -1 осуществляется т. н. бифуркации удвоения периода (табл. 2, строка 1). Она характеризуется тем, что в бифуркац. момент малое по модулю возмущение через период просто меняет знак, а через следующий оборот в линейном приближении происходит замыкание траектории. В результате этой бифуркации из исходного периодич. движения рождается устойчивое периодич. движение приблизительно удвоенного периода, а исходный режим становится неустойчивым. Появлению двухчастотных колебаний в физ. системе отвечает бифуркации рождения двумерного тора из периодич. траектории (табл. 2, строка 2). В системах, зависящих от двух параметров, или в системах с оп-редел. типом симметрии встречается бифуркации, при к-рой рождается сразу 2 устойчивых предельных цикла (табл. 2, строка 3).

Бифуркации, в результате к-рых исчезают статич. или периодич. режимы (т. е. состояния равновесия или предельные циклы), могут приводить к тому, что динамич. система переходит в режим стохастических колебаний. Термин "бифуркация" иногда используют для обозначения перестроек таких объектов, к-рые не меняются во времени; в этом случае употребляется также термин "катастрофа" (см. Катастроф теория).

Литература по бифуркациям

Андронов А. А., Витт А. А., Хайкин С. Э., Теория колебаний, 3 изд., M., 1981;
Теория бифуркаций динамических систем на плоскости, M., 1967,
Арнольд В. И., Дополнительные главы теории обыкновенных дифференциальных уравнений, M., 1978
его же, Теория катастроф, 2 изд., M., 1983
Mарсден Д., Mак - Кракен M., Бифуркация рождения цикла и ее приложения, пер. с англ., M , 1980;
Xакен X., Синергетика, пер. с англ., M , 1980
Рабинович М. И., Трубецков Д. И., Введение в теорию колебаний и волн, M., 1984.

В. С. Афраймович, M. И. Рабинович

к библиотеке к оглавлению FAQ по эфирной физике ТОЭЭ ТЭЦ ТПОИ ТИ

Знаете ли Вы, что любой разумный человек скажет, что не может быть улыбки без кота и дыма без огня, что-то там, в космосе, должно быть, теплое, излучающее ЭМ-волны, соответствующее температуре 2.7ºК. Действительно, наблюдаемое космическое микроволновое излучение (CMB) есть тепловое излучение частиц эфира, имеющих температуру 2.7ºK. Еще в начале ХХ века великие химики и физики Д. И. Менделеев и Вальтер Нернст предсказали, что такое излучение (температура) должно обнаруживаться в космосе. В 1933 году проф. Эрих Регенер из Штуттгарта с помощью стратосферных зондов измерил эту температуру. Его измерения дали 2.8ºK - практически точное современное значение. Подробнее читайте в FAQ по эфирной физике.

НОВОСТИ ФОРУМА

Рыцари теории эфира