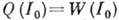 .
.Автоколебания - незатухающие колебания в дис-сипативной нелинейной системе, поддерживаемые за счёт энергии
внеш. источника, параметры к-рых (амплитуда, частота, спектр колебаний) определяются
свойствами самой системы и не зависят от конечного изменения нач. условий. Термин
"А." введён А. А. Андроновым в 1928.
Автоколебания принципиально отличаются от др. колебат.
процессов в диссипативных системах тем, что для их поддержания не требуется
колебат. воздействий извне. Примеры А.: колебания скрипичной струны при движении
смычка, тока в радиотехн. генераторе, воздуха в органной трубе, маятника в часах.
Возникают А. в результате развития колебат. неустойчивостей с их последующей
стабилизацией из-за прекращения поступления энергии от источника или прогрессирующего
возрастания потерь (диссипации). Режим стационарных А. определяется из условия
энергетич. баланса - в ср. за период диссипативные траты энергии Q (I) (I - интенсивность А.) должны точно компенсироваться поступлением энергии W(I)от источника:  .
.
Если в окрестности стационарного режима
I0 энергия потерь Q (I) при изменении I
растёт быстрее, чем приток энергии W(I), то этот режим А., с энергетич.
точки зрения, устойчив (рис. 1, а); если же быстрее увеличивается W(I), то
стационарный режим неустойчив (рис. 1, б). Даже в тех случаях, когда можно ввести
функции Q и W, они обычно зависят не только от интенсивностей А.,
но и от их фаз, поэтому энергетич. метод определения устойчивости А. в общем
случае неприменим. Системы, в к-рых А. возникают "самопроизвольно"
- без нач. толчка, наз. системами с мягким режимом возбуждения; если для
возникновения А. необходим конечный нач.
толчок, то говорят о жёстком режиме возбуждения.
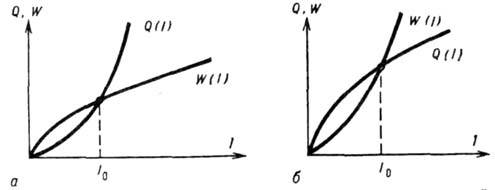
Рис. 1. Энергетическая схема установления
автоколебаний: а - стационарный
режим устойчив; б - стационарный режим неустойчив.
В простейших автоколебат. системах можно
выделить колебат. систему с затуханием, усилитель колебаний, нелинейный ограничитель
и звено обратной связи. Напр., в ламповом генераторе (генераторе Ван дер Поля,
рис. 2, а, б)колебат. контур с потерями, состоящий из ёмкости С, индуктивности L и сопротивления R, представляет собой диссипативную
колебат. систему, цепь катод - сетка и индуктивность L образуют
цепь обратной связи.
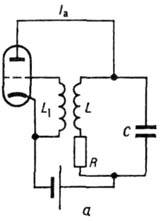
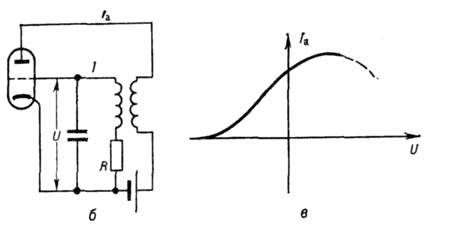
Рис. 2. Схемы генераторов Ван дер Поля:
а - с колебательным контуром в цепи анода; б - с колебательным
контуром в цепи сетки; в - характеристика лампы.
Случайно возникшие в колебат. контуре
малые собств. колебания через катушку L управляют анодным током лампы,
к-рая является усилителем. При положит. обратной связи (т. е. при определённом
взаимном расположении катушек L и L1) в контур вносится
определ. энергия. Если эта энергия больше энергии потерь в контуре, то амплитуда
малых вначале колебаний в контуре нарастает. Поскольку анодный ток лампы зависит
от напряжения на сетке нелинейным образом (рис. 2, в), то при нарастании амплитуды
колебаний энергия, поступающая в контур, уменьшается и при нек-рой амплитуде
колебаний становится равной энергии потерь. В результате устанавливается режим
стационарных А., при к-ром внеш. источник (анодная батарея) компенсирует все
потери энергии. Т. о., автоколебат. системы должны быть принципиально нелинейными
- именно нелинейность не позволяет колебаниям безгранично нарастать, управляя
поступлением и тратами энергии источника.
Чтобы определить характер А. и зависимость
их амплитуды и формы от параметров системы, необходимо обратиться к анализу
соответствующей математической модели. Для простейшего генератора (рис.
2, а) такой моделью служит уравнение Ван
дер Поля
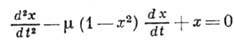 (1),
(1),
к-рое получается при пренебрежении сеточными
токами лампы и аппроксимации её характеристики кривой, представленной на рис.
2, в. Это ур-ние записано в безразмерных переменных, где 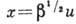 ;
; 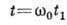 ;
; 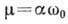 . Здесь
. Здесь 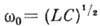 - собств.
частота колебат. контура,
- собств.
частота колебат. контура, 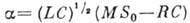 - параметр превышения над порогом генерации (при
- параметр превышения над порогом генерации (при 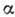 <0
потеря в контуре больше, чем вносимая энергия),
<0
потеря в контуре больше, чем вносимая энергия),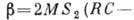
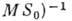 характеризует амплитуду А., М - коэфф. взаимной индукции, S0 и S2 - параметры вольт-амперной характеристики усилит.
лампы. Тот факт, что А. в рассматриваемой системе описываются диф-ференц. ур-нием
2-го порядка (его фазовое пространство - плоскость), сразу накладывает
принцип. ограничения на вид А. В подобных системах возможны только периодич.
А.
характеризует амплитуду А., М - коэфф. взаимной индукции, S0 и S2 - параметры вольт-амперной характеристики усилит.
лампы. Тот факт, что А. в рассматриваемой системе описываются диф-ференц. ур-нием
2-го порядка (его фазовое пространство - плоскость), сразу накладывает
принцип. ограничения на вид А. В подобных системах возможны только периодич.
А.
Геом. образом установившихся А. в фазовом
пространстве системы служит аттрактор - траектория (или множество траекторий),
расположенная в огранич. области фазового пространства и притягивающая к себе
все близкие траектории. Поскольку на фазовой плоскости траектории пересекаться
не могут, в системах 2-го порядка может существовать лишь простейший нетривиальный
аттрактор - замкнутая траектория, к к-рой стремятся все ближайшие траектории.
Такая траектория наз. предельным циклом, к-рый служит образом периодич. А. Размеры
предельного цикла определяют амплитуду А., время движения изображающей точки
по циклу - период А., а форма предельного цикла - форму колебаний. Величина
(J, характеризует нелинейность системы: чем больше нелинейность, тем больше
форма колебаний отличается от синусоидальной (рис. 3). При малых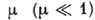 потери в контуре и вносимая в него энергия
очень малы - ур-ние (1) близко к ур-нию гармонич. осциллятора, а А. близки к
синусоидальным с частотой
потери в контуре и вносимая в него энергия
очень малы - ур-ние (1) близко к ур-нию гармонич. осциллятора, а А. близки к
синусоидальным с частотой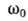 .
.
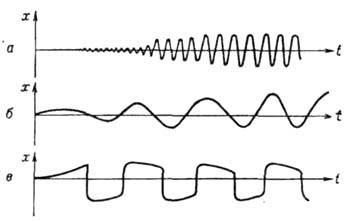
Рис. 3. Осциллограммы х (t),
иллюстрирующие характер установления и форму автоколебаний в системе (1) соответственно:
при 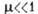 - квазигармонические колебания (а); при
- квазигармонические колебания (а); при 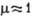 - сильно не-синусоидальные колебания (б); при
- сильно не-синусоидальные колебания (б); при 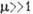 - релаксационные колебания (в).
- релаксационные колебания (в).
В др. предельном случае 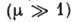 потери в контуре и вносимая в него энергия очень велики по сравнению с энергией
в нём запасённой, поэтому колебания будут сильно отличаться от синусоидальных,
превращаясь в релаксационные. Анализ таких А. удобно проводить, разделяя движения
на участки быстрых и медленных движений (см. Релаксационные колебания).
потери в контуре и вносимая в него энергия очень велики по сравнению с энергией
в нём запасённой, поэтому колебания будут сильно отличаться от синусоидальных,
превращаясь в релаксационные. Анализ таких А. удобно проводить, разделяя движения
на участки быстрых и медленных движений (см. Релаксационные колебания).
При изменении величины параметра 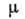 не происходит никаких качественных изменений в структуре разбиения фазовой плоскости
ур-ния (1) на траектории - при любом
не происходит никаких качественных изменений в структуре разбиения фазовой плоскости
ур-ния (1) на траектории - при любом 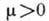 в системе имеются единств. состояние равновесия (х=0,
в системе имеются единств. состояние равновесия (х=0, 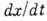 =0),
к-рое неустойчиво, и единств. предельный цикл, к-рый устойчив. Качественные
перестройки - бифуркации происходят лишь при смене знака
=0),
к-рое неустойчиво, и единств. предельный цикл, к-рый устойчив. Качественные
перестройки - бифуркации происходят лишь при смене знака 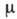 .
Рассмотренная картина соответствует мягкому режиму возникновения А., к-рому
соответствует фазовый портрет, изображённый на рис. 4, а. В системах
с жёстким режимом возбуждения колебания самопроизвольно нарастают лишь с нек-рой
нач. амплитудой, т. е. когда имеется толчок с амплитудой, большей нек-рого критич.
значения; при этом на фазовом, портрете (рис. 5) нач. точка должна лежать вне
заштрихованной области, т. е. изображающая точка должна быть выведена за пределы
области притяжения устойчивого состояния равновесия, границей к-рого служит
неустойчивый предельный цикл.
.
Рассмотренная картина соответствует мягкому режиму возникновения А., к-рому
соответствует фазовый портрет, изображённый на рис. 4, а. В системах
с жёстким режимом возбуждения колебания самопроизвольно нарастают лишь с нек-рой
нач. амплитудой, т. е. когда имеется толчок с амплитудой, большей нек-рого критич.
значения; при этом на фазовом, портрете (рис. 5) нач. точка должна лежать вне
заштрихованной области, т. е. изображающая точка должна быть выведена за пределы
области притяжения устойчивого состояния равновесия, границей к-рого служит
неустойчивый предельный цикл.
Рис. 4. Фазовые портреты системы (1):
а - при  ; б - при
; б - при  ;
в - при
;
в - при 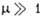 .
.
В системах, даже незначительно более
сложных, чем генератор на рис. 2, а, напр. в системах с полутора степенями
свободы, возможны не только периодич. и квазипериодич. А. (с несколькими несоизмеримыми
частотами), но и А., ничем неотличимые от случайных - т. н. стохастические А.
Примером такой автоколебат. системы - генератора шума, в к-ром хаотич. колебания
(колебания со сплошным спектром) совершаются в диссипативной системе за счёт
энергии регулярных источников, может служить генератор на рис. 2, б, если
в контур последовательно с индуктивностью добавлен нелинейный элемент с невзаимно
однозначной вольт-амперной характеристикой (рис. 6). Таким элементом является,
напр., туннельный диод .Матем. модель или соответствующая такому генератору
динамическая система может быть представлена в виде системы 3-го порядка:
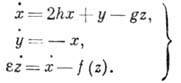 (2)
(2)
Здесь х, у, z - соответственно
безразмерные токи в контуре, напряжение на ёмкости и напряжение на туннельном
диоде, h - инкремент нарастания колебаний в контуре в отсутствие диода,
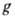 характеризует степень
влияния диода на процессы в контуре,
характеризует степень
влияния диода на процессы в контуре,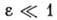 - малый параметр, пропорциональный ёмкости туннельного диода, f(z) -
его нормированная характеристика.
- малый параметр, пропорциональный ёмкости туннельного диода, f(z) -
его нормированная характеристика.
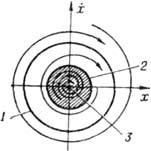
Рис. 5. Фазовый портрет, отвечающий жёсткому возбуждению автоколебаний: 1 - устойчивый предельный цикл; 2 - неустойчивый предельный цикл; 3 - устойчивое состояние равновесия.
Фазовое пространство системы (2) трёхмерно. При определ. параметрах в этом фазовом пространстве все траектории будут входить в ограниченную область, внутри к-рой нет ни устойчивых состояний равновесия, ни устойчивых предельных циклов. Внутри этой области содержится притягивающее множество траекторий, каждая из к-рых неустойчива,- это т. н. странный аттрактор. Подобно тому, как предельный цикл является образом периодич. А., образом стохастич. А. служит странный аттрактор. Для автоколебат. систем с неск. степенями свободы характерны такие явления, как синхронизация и конкуренция колебаний. Разделяют внеш. синхронизацию А., или захватывание частоты генератора, и взаимную синхронизацию. При захватывании частоты устанавливаются А. с частотой и фазой, соответствующими частоте и фазе внеш. периодич. воздействия, а при взаимной синхронизации - периодич. сфазированные колебания в ансамбле подсистем, к-рые в независимом режиме работы характеризуются разл. частотами. Захватывание частоты широко используется для управления и стабилизации частоты мощных малостабильных генераторов с помощью высокостабильных маломощных (напр., в лазерах).

Рис. 6. Вольт-амперная характеристика туннельного диода.
Полоса захватывания
- область расстроек между частотами собств. колебаний и внеш. сигналом, внутри
к-рой устанавливается режим синхронизации,- расширяется при увеличении амплитуды
внеш. воздействия. Вне границы
захватывания устойчивый режим генерации периодич. колебаний сменяется режимом
биений - режимом квазипериодич. колебаний либо стохастич. режимом. Взаимная
синхронизация подсистем или различных элементарных колебаний (мод) используется
при работе неск. генераторов на общую нагрузку, для получения коротких импульсов
в многомодовых генераторах (напр., лазерах) и т. д.
Конкуренция мод - подавление одних мод другими в автоколебат. системах -
связана с тем, что конкурирующие моды черпают энергию на покрытие
дисси-пативных расходов из общего источника. В результате одни моды
создают дополнит. нелинейное затухание для других. Благодаря эффектам
конкуренции и взаимной синхронизации колебаний в автоколебат. системах с
большим числом степеней свободы (или даже бесконечным числом - в случае
распределённых систем) возможно установление из нач. шума (нарастающих в
результате развития линейных неустойчивостей флуктуации на разл.
частотах) режима регулярных периодич. А. Эффекты конкуренции и
синхронизации оказываются принципиальными и для появления
высокоорганизованных структур в нелинейных не равновесных средах.
В распределённых системах характер А. существенно зависит, помимо вида нелинейности, ещё и от особенностей дисперсии среды и граничных условий, в частности наличия резонатора. В нек-рых случаях спектр возбуждения мод и особенности их нелинейного взаимодействия таковы, что при анализе А. в распределённой системе с бесконечным числом степеней свободы возможно ограничиться т. н. одно-модовым описанием.
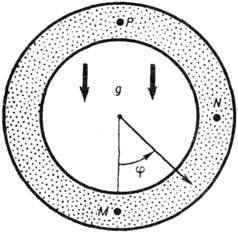
Рис. 7. Кольцевая труба, заполненная жидкостью,- конвективная петля; g- ускорение силы тяжести, ТН - температуpa в точке М, TВ - температуpa в точке Р.
Для примера рассмотрим А. в кольцевом
резонаторе - расположенной в вертик. плоскости замкнутой трубе, заполненной
вязкой жидкостью (рис. 7). При подогреве кольца снизу в системе устанавливается
режим конвекции: более лёгкая, нагретая в основании кольца часть жидкости всплывает,
заставляя охлаждённую жидкость опускаться вниз.
Т. о., начиная с нек-рой разности температур ТВ - ТН= 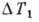 устанавливается режим стационарного вращения жидкости по или против часовой
стрелки. При этом вся жидкость вращается как целое - реализуется лишь одно наиб.
крупномасштабное движение. Дальнейшее увеличение
устанавливается режим стационарного вращения жидкости по или против часовой
стрелки. При этом вся жидкость вращается как целое - реализуется лишь одно наиб.
крупномасштабное движение. Дальнейшее увеличение 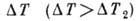 приводит к возникновению А., проявляющихся в том, что жидкое кольцо внутри трубы
время от времени будет менять направление своего движения. Физически это можно
пояснить так: пусть в данный момент жидкость движется по часовой стрелке, при
достаточно большом
приводит к возникновению А., проявляющихся в том, что жидкое кольцо внутри трубы
время от времени будет менять направление своего движения. Физически это можно
пояснить так: пусть в данный момент жидкость движется по часовой стрелке, при
достаточно большом 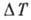 архимедова сила велика и водяное кольцо ускоряется настолько, что остывший вверху
жидкий объём, пройдя горячее основание и не успев нагреться, уже не достигает
верх. части кольца и приостанавливается (архимедова сила недостаточна, чтобы
преодолеть силу вязкости и гравитации). При этом опускающаяся (правая) часть
жидкости теплее и, следовательно, легче поднимающейся.
архимедова сила велика и водяное кольцо ускоряется настолько, что остывший вверху
жидкий объём, пройдя горячее основание и не успев нагреться, уже не достигает
верх. части кольца и приостанавливается (архимедова сила недостаточна, чтобы
преодолеть силу вязкости и гравитации). При этом опускающаяся (правая) часть
жидкости теплее и, следовательно, легче поднимающейся.
В результате торможения жидкого кольца
жидкость в его основании нагревается и всплывает, но уже в противоположном направлении
- давление справа меньше, чем слева. Т. о., жидкое кольцо меняет направление
своего вращения и начинает закручиваться против часовой стрелки. Затем всё повторяется
в обратном порядке. Такие вызываемые тепловой конвекцией А. могут быть как периодическими,
так и стохастическими. Поскольку никакие другие масштабы движения, кроме основного,
в А. рассматриваемого вида не участвуют, матем. модель для описания этих А.
может быть получена из исходных ур-ний гидродинамики в предположении, что зависимость
полей скорости и температуры от пространственных координат не меняется во времени
и пропорциональна 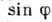 ,
где
,
где 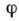 - угл. координата
элементарного объёма жидкости. В результате для безразмерных скорости x(t)движения жидкого кольца, температуры y(t)жидкости в точке N и
температуры z(t)в точке М можно получить систему ур-ний в обыкновенных
производных:
- угл. координата
элементарного объёма жидкости. В результате для безразмерных скорости x(t)движения жидкого кольца, температуры y(t)жидкости в точке N и
температуры z(t)в точке М можно получить систему ур-ний в обыкновенных
производных:
 (3),
(3),
где 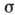 ,
, 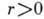 . Это - известная система Лоренца (см. Лоренца система ),к-рая является одной из осн. моделей теории стохастич. А. В зависимости от параметров
. Это - известная система Лоренца (см. Лоренца система ),к-рая является одной из осн. моделей теории стохастич. А. В зависимости от параметров 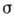 и
и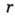 в фазовом пространстве системы (3) могут существовать как устойчивый предельный цикл, так и странный аттрактор.
в фазовом пространстве системы (3) могут существовать как устойчивый предельный цикл, так и странный аттрактор.
В общем случае А. в резонаторах, к-рые описываются ур-ниями в частных производных с соответствующими граничными условиями, невозможно представить с помощью конечномерной динамич. системы. Однако, как правило, благодаря разного рода физ. обстоятельствам, напр. наличию диссипации, прогрессирующей с ростом частоты или уменьшением пространственного масштаба пульсаций, такое конечномерное описание оказывается справедливым.
В неравновесных диссипативных средах, помимо А., о к-рых речь шла выше, возможны ещё т. н. авто-волны и автоструктуры - не связанные с граничными условиями пространственно-временные образования, параметры к-рых определяются лишь свойствами нелинейной неравновесной среды, напр. уединённые фронты горения и волны популяций, импульсы в нервных волокнах, цилиндрические и спиральные волны в сердечной ткани и др. Стохастич. А. в нелинейных неравновесных средах - это турбулентность.

Понятие же "физического вакуума" в релятивистской квантовой теории поля подразумевает, что во-первых, он не имеет физической природы, в нем лишь виртуальные частицы у которых нет физической системы отсчета, это "фантомы", во-вторых, "физический вакуум" - это наинизшее состояние поля, "нуль-точка", что противоречит реальным фактам, так как, на самом деле, вся энергия материи содержится в эфире и нет иной энергии и иного носителя полей и вещества кроме самого эфира.
В отличие от лукавого понятия "физический вакуум", как бы совместимого с релятивизмом, понятие "эфир" подразумевает наличие базового уровня всей физической материи, имеющего как собственную систему отсчета (обнаруживаемую экспериментально, например, через фоновое космичекое излучение, - тепловое излучение самого эфира), так и являющимся носителем 100% энергии вселенной, а не "нуль-точкой" или "остаточными", "нулевыми колебаниями пространства". Подробнее читайте в FAQ по эфирной физике.
|
|