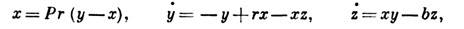
Лоренца система - система трёх нелинейных дифференц. ур-ний первого порядка:
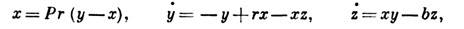
решения к-рой в широкой
области параметров являются нерегулярными функциями времени и по мн. своим характеристикам
неотличимы от случайных. Л. с. была получена Э. Лоренцем (Е. Lorenz) из ур-ний
гидродинамики как модель для описания тепловой конвекции в горизонтальном слое
жидкости, подогреваемой снизу (Рr - Прандтля число, 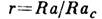 - приведённое Рэ-лея число, b - определяется выбором моды
в Фурье-разложении поля скорости и температуры).
- приведённое Рэ-лея число, b - определяется выбором моды
в Фурье-разложении поля скорости и температуры).
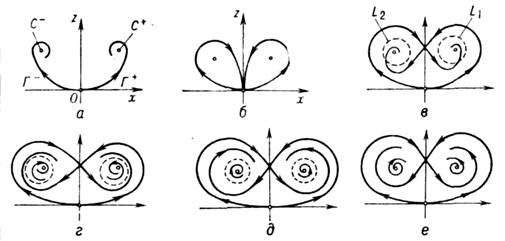
Рис. 1. Иллюстрация последовательных
бифуркаций в системе Лоренца при увеличении параметра r: а) 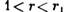 ; б)
; б) 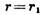 ;
в)
;
в)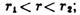 г)
г)
 д)
д)
 е)
е)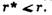
Л. с.- один из примеров
динамической системы, имеющей простой физ. смысл; она демонстрирует стохастич.
поведение системы. В фазовом пространстве этой системы в области параметров,
указанных на рис. 1, существует странный аттрактор ,движение изображающей
точки на к-ром соответствует "случайному" - турбулентному течению
жидкости при тепловой конвекции.
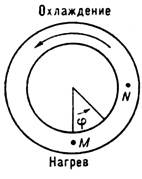
Рис. 2. Конвективная петля - физическая модель, для которой выводятся уравнения Лоренца.
Л. с. (при b=l)
описывает, в частности, движение жидкости в конвективной петле, расположенной
в вертикальной плоскости
в однородном поле тяжести тороидальной полости, заполненной жидкостью (рис.
2). На стенках полости поддерживается не зависящая от времени (но зависящая
от угла 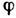 )
темп-pa Т(
)
темп-pa Т(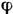 );
ниж. часть петли теплее верхней. Ур-ния движения жидкости в конвективной петле
сводятся к Л. с., где x(t] - скорость движения жидкости, у (t) - темп-pa
в точке N, a z(t) - темп-pa в точке М при больших t. С ростом г характер движения жидкости меняется: сначала (при г<1)
жидкость неподвижна, далее (при
);
ниж. часть петли теплее верхней. Ур-ния движения жидкости в конвективной петле
сводятся к Л. с., где x(t] - скорость движения жидкости, у (t) - темп-pa
в точке N, a z(t) - темп-pa в точке М при больших t. С ростом г характер движения жидкости меняется: сначала (при г<1)
жидкость неподвижна, далее (при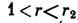 ) устанавливается циркуляция с пост. скоростью (либо по часовой стрелке, либо
против); при ещё больших r всё течение становится чувствительным к малым
изменениям нач. условий, скорость циркуляции жидкости меняется уже нерегулярно:
жидкость вращается иногда по часовой стрелке, иногда - против.
) устанавливается циркуляция с пост. скоростью (либо по часовой стрелке, либо
против); при ещё больших r всё течение становится чувствительным к малым
изменениям нач. условий, скорость циркуляции жидкости меняется уже нерегулярно:
жидкость вращается иногда по часовой стрелке, иногда - против.
При обычно используемых
значениях Pr=10, b=8/3 Л. с. обладает след. свойствами: ур-ния
Л. с. инварианты относительно преобразования  ,
,

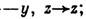 фазовый объём сокращается с пост. скоростью
фазовый объём сокращается с пост. скоростью
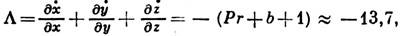
за единицу времени объём
сокращается в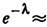 106 раз. С ростом г в Л. с. происходят след. осн. бифуркации. 1) При
106 раз. С ростом г в Л. с. происходят след. осн. бифуркации. 1) При 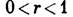 единственным состоянием равновесия является
устойчивый узел в начале координат О (О, О, 0). 2) При
единственным состоянием равновесия является
устойчивый узел в начале координат О (О, О, 0). 2) При  , где r1=13,92, Л. с. кроме упомянутого тривиального (О)имеет ещё два состояния равновесия
, где r1=13,92, Л. с. кроме упомянутого тривиального (О)имеет ещё два состояния равновесия 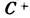 ,
,
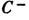 . Состояние
равновесия О является седлом, имеющим двумерное устойчивое многообразие
и одномерное неустойчивое, состоящее из О и двух сепаратрис
. Состояние
равновесия О является седлом, имеющим двумерное устойчивое многообразие
и одномерное неустойчивое, состоящее из О и двух сепаратрис 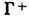 и
и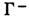 , стремящихся
к
, стремящихся
к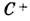 и
и
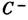 (рис.
1, а). 3) При r=r1 каждая из сепаратрис становится
двоякоасимпто-тической к седлу О (рис. 1, б). При переходе r через
r1 из замкнутых петель сепаратрис рождаются неустойчивые (седловые)
периодич. движения - предельные циклы L1 и L2. Вместе с этими неустойчивыми циклами рождается и очень сложно организованное
предельное множество; оно, однако, не является притягивающим (аттрактором),
и при
(рис.
1, а). 3) При r=r1 каждая из сепаратрис становится
двоякоасимпто-тической к седлу О (рис. 1, б). При переходе r через
r1 из замкнутых петель сепаратрис рождаются неустойчивые (седловые)
периодич. движения - предельные циклы L1 и L2. Вместе с этими неустойчивыми циклами рождается и очень сложно организованное
предельное множество; оно, однако, не является притягивающим (аттрактором),
и при 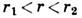 (рис.
1, в), где r2=24,06, все траектории по-прежнему стремятся
к
(рис.
1, в), где r2=24,06, все траектории по-прежнему стремятся
к . Эта
ситуация отличается от предшествующей тем, что теперь сепаратрисы
. Эта
ситуация отличается от предшествующей тем, что теперь сепаратрисы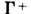 _ и
_ и 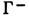 идут
к "не своим" состояниям равновесия
идут
к "не своим" состояниям равновесия  и
и 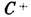 соответственно.
4) При
соответственно.
4) При 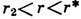 ,
гдо
,
гдо 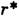 = 24,74, в Л. с. наряду с устойчивыми состояниями равновесия
= 24,74, в Л. с. наряду с устойчивыми состояниями равновесия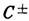 существует
ещё притягивающее множество, характеризующееся сложным поведением траекторий,-
аттрактер Лоренца (рис. 1, д и рис. 3). 5) При
существует
ещё притягивающее множество, характеризующееся сложным поведением траекторий,-
аттрактер Лоренца (рис. 1, д и рис. 3). 5) При  седловые циклы L1 и L2 стягиваются
к состояниям равновесия
седловые циклы L1 и L2 стягиваются
к состояниям равновесия 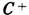 и
и 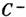 ,
к-рые при
,
к-рые при  теряют
устойчивость, и при
теряют
устойчивость, и при 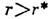 единственным притягивающим мно-
единственным притягивающим мно-
жеством Л. с. является
аттрактор Лоренца. Т. о., если стремить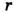 к
к 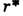 со
стороны меньших значений, то стохастичность в Л. с. возникает сразу, скачком,
т. е. имеет место жёсткое возникновение стохастичности.
со
стороны меньших значений, то стохастичность в Л. с. возникает сразу, скачком,
т. е. имеет место жёсткое возникновение стохастичности.
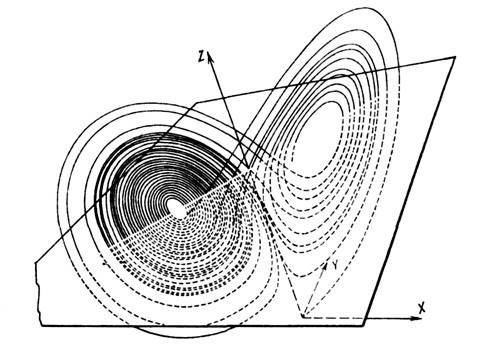
Рис. 3. Траектория, воспроизводящая аттрактор Лоренца (выходит из начала координат); горизонтальная плоскость соответствует r = = 27, r=28.
К Л. с. сводятся не только ур-ния, описывающие конвективные движения жидкости, но и др. физ. модели (трёхуровневый лазер, дисковое динамо и т. д.).

В. Г. Шехов
1. Электромагнитная волна (в религиозной терминологии релятивизма - "свет") имеет строго постоянную скорость 300 тыс.км/с, абсурдно не отсчитываемую ни от чего. Реально ЭМ-волны имеют разную скорость в веществе (например, ~200 тыс км/с в стекле и ~3 млн. км/с в поверхностных слоях металлов, разную скорость в эфире (см. статью "Температура эфира и красные смещения"), разную скорость для разных частот (см. статью "О скорости ЭМ-волн")
2. В релятивизме "свет" есть мифическое явление само по себе, а не физическая волна, являющаяся волнением определенной физической среды. Релятивистский "свет" - это волнение ничего в ничем. У него нет среды-носителя колебаний.
3. В релятивизме возможны манипуляции со временем (замедление), поэтому там нарушаются основополагающие для любой науки принцип причинности и принцип строгой логичности. В релятивизме при скорости света время останавливается (поэтому в нем абсурдно говорить о частоте фотона). В релятивизме возможны такие насилия над разумом, как утверждение о взаимном превышении возраста близнецов, движущихся с субсветовой скоростью, и прочие издевательства над логикой, присущие любой религии.
4. В гравитационном релятивизме (ОТО) вопреки наблюдаемым фактам утверждается об угловом отклонении ЭМ-волн в пустом пространстве под действием гравитации. Однако астрономам известно, что свет от затменных двойных звезд не подвержен такому отклонению, а те "подтверждающие теорию Эйнштейна факты", которые якобы наблюдались А. Эддингтоном в 1919 году в отношении Солнца, являются фальсификацией. Подробнее читайте в FAQ по эфирной физике.
|
|