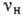 )
нелинейной среды, к-рой может быть газ, жидкость, твёрдое тело, плазма (рис.
1).
)
нелинейной среды, к-рой может быть газ, жидкость, твёрдое тело, плазма (рис.
1).Вынужденное рассеяние света - рассеяние света на индуцированных самой рассеиваемой
волной элементарных возбуждениях среды (оптич. и акустич. фононах, магнонах,
электронах, температурных волнах и т. п.).
Причина вынужденного рассеяния света - обратное воздействие
световых волн на рассеивающую среду, обусловленное её оптич. нелинейностью.
При спонтанном рассеянии это воздействие пренебрежимо мало, так что рассеяние
происходит на равновесных тепловых флуктуациях.
Возможность вынужденного рассеяния света была
теоретически предсказана Г. Плачеком (G. Placzek) ещё в 1934. Однако первые
успешные эксперименты были проведены лишь в 1962 после появления лазеров.
Вынужденное рассеяние света обычно наблюдается при облучении интенсивным лазерным излучением (при
накачке с частотой 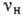 )
нелинейной среды, к-рой может быть газ, жидкость, твёрдое тело, плазма (рис.
1).
)
нелинейной среды, к-рой может быть газ, жидкость, твёрдое тело, плазма (рис.
1).
Вынужденное рассеяние света так же, как и
спонтанное, связано с модуляцией параметров среды (напр., электронной поляризуемости,
показателя преломления и т. п.) при её возбуждении светом, что приводит к амплитудной
модуляции рассеянного
света, а следовательно, к появлению в нём новых спектральных компонент (стоксовых
и антистоксовых с частотами 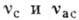 соответственно). Однако в отличие от спонтанного рассеяния света
при вынужденном рассеянии света происходит взаимодействие излучения накачки и рассеянного света через
среду, поэтому элементарные возбуждения становятся когерентными [1, 2, 3).
соответственно). Однако в отличие от спонтанного рассеяния света
при вынужденном рассеянии света происходит взаимодействие излучения накачки и рассеянного света через
среду, поэтому элементарные возбуждения становятся когерентными [1, 2, 3).
Наиб. характерные признаки вынужденного рассеяния света - это резкое возрастание интенсивности и сужение диаграмм направленности
стоксовых и антистоксовых компонент. В случае вынужденного рассеяния света интенсивности рассеянных
компонент сравнимы с интенсивностью излучения накачки (при спонтанном рассеянии
они составляют ~10-5-10-6 интенсивности рассеиваемой волны).
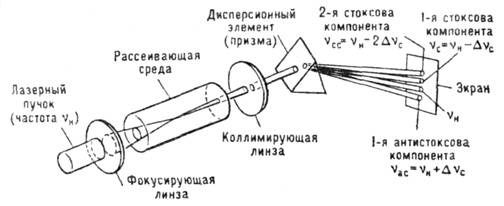
Рис. 1. Типичная схема опыта по наблюдению вынужденного комбинационного рассеяния света.
На классич. языке вынужденного рассеяния света проще всего объяснить на примере одного из наиб. важных
типов - вынужденного комбинац. рассеяния (BKP) на колебат. переходах молекул
[4]. Описание взаимодействия света с внутримолекулярными движениями основывается
на учёте зависимости электронной поляризуемости молекул 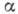 от ядерной конфигурации, определяемой координатами ядер, а именно амплитудой
их колебаний qi (подробнее см. Комбинационное рассеяние
света). В простейшем одномерном случае (i=1)
от ядерной конфигурации, определяемой координатами ядер, а именно амплитудой
их колебаний qi (подробнее см. Комбинационное рассеяние
света). В простейшем одномерном случае (i=1)
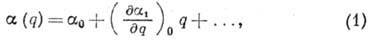
где 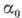 - линейная поляризуемость. Наличие члена
- линейная поляризуемость. Наличие члена 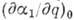 в (1) является причиной модуляции света молекулярными колебаниями: в наведённой
световой волной поляризации P появляются новые частотные компоненты,
сдвинутые на частоту колебаний ядер (т. е. на собственную частоту колебаний
молекулы):
в (1) является причиной модуляции света молекулярными колебаниями: в наведённой
световой волной поляризации P появляются новые частотные компоненты,
сдвинутые на частоту колебаний ядер (т. е. на собственную частоту колебаний
молекулы):

В условиях, когда q
определяется тепловыми движениями в среде, (2) описывает спонтанное комбинац.
рассеяние.
Зависимость  является одновременно причиной обратного воздействия световых волн на молекулярные
колебания. Действительно, энергия взаимодействия W молекулы со световой
волной выражается в виде
является одновременно причиной обратного воздействия световых волн на молекулярные
колебания. Действительно, энергия взаимодействия W молекулы со световой
волной выражается в виде
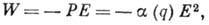
и, следовательно, при 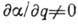 в световом поле возникает сила
в световом поле возникает сила
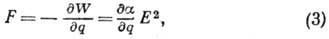
действующая на колебания.
Если световое поле, падающее на среду, такой частоты 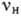 ,
что
,
что 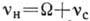 , где
, где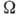 -
собственная частота молекулярных колебаний,
-
собственная частота молекулярных колебаний, 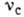 - стоксова компонента, то эта сила может привести к резонансной раскачке колебаний
частоты
- стоксова компонента, то эта сила может привести к резонансной раскачке колебаний
частоты 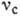 , возникновению
параметрической неустойчивости, т. н. распадной неустойчивости. В этих
условиях на хаотич. внутримолекулярное движение накладываются регулярные вынужденные
колебания, фазы к-рых в разл. молекулах определяются фазами компонент светового
поля (происходит фазирование
молекулярных колебаний во всём объёме, занятом световыми полями). Неустойчивость
возникает, если интенсивность
, возникновению
параметрической неустойчивости, т. н. распадной неустойчивости. В этих
условиях на хаотич. внутримолекулярное движение накладываются регулярные вынужденные
колебания, фазы к-рых в разл. молекулах определяются фазами компонент светового
поля (происходит фазирование
молекулярных колебаний во всём объёме, занятом световыми полями). Неустойчивость
возникает, если интенсивность 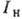 световой волны превышает нек-рое пороговое значение:
световой волны превышает нек-рое пороговое значение: 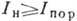 В этом случае низкочастотная стоксова компонента экспоненциально усиливается
по мере распространения через среду:
В этом случае низкочастотная стоксова компонента экспоненциально усиливается
по мере распространения через среду: 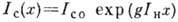 . Здесь
. Здесь 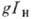 - инкремент усиления, g - коэф. усиления, х - длина возбуждённой части
среды. В практич. случаях
- инкремент усиления, g - коэф. усиления, х - длина возбуждённой части
среды. В практич. случаях 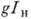 может достигать величины ~102.
может достигать величины ~102.
В силу (3) амплитуда возбуждённых
световой волной молекулярных колебаний 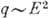 и, следовательно, для поляризации среды можно записать, согласно (2),
и, следовательно, для поляризации среды можно записать, согласно (2),
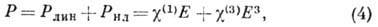
где  - кубич. нелинейная восприимчивость. Именно она является универсальной характеристикой
среды, описывающей явления вынужденного рассеяния света (см. Нелинейная оптика).
- кубич. нелинейная восприимчивость. Именно она является универсальной характеристикой
среды, описывающей явления вынужденного рассеяния света (см. Нелинейная оптика).
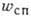 (с-1) пропорциональна интенсивности
(с-1) пропорциональна интенсивности 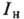 (Вт/см2) света накачки:
(Вт/см2) света накачки: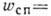
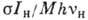 ,
где
,
где 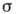 (см2)
- сечение рассеяния, а величина
(см2)
- сечение рассеяния, а величина 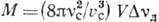 представляет собой число мод в облучаемом объёме V,
представляет собой число мод в облучаемом объёме V, 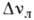 -ширина
спектральной линии спонтанного рассеяния,
-ширина
спектральной линии спонтанного рассеяния,  -скорость
рассеянного света в нелинейной среде. Полная вероятность спонтанного рассеяния
-скорость
рассеянного света в нелинейной среде. Полная вероятность спонтанного рассеяния
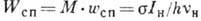 . Рассеяние становится
вынужденным, если в данной моде уже находится
. Рассеяние становится
вынужденным, если в данной моде уже находится  1
рассеявшихся фотонов. В соответствии со статистикой Бозе - Эйнштейна, к-рой
подчиняются фотоны, рассеивающийся фотон стремится попасть в ту моду, где уже
есть аналогичные фотоны.
1
рассеявшихся фотонов. В соответствии со статистикой Бозе - Эйнштейна, к-рой
подчиняются фотоны, рассеивающийся фотон стремится попасть в ту моду, где уже
есть аналогичные фотоны.
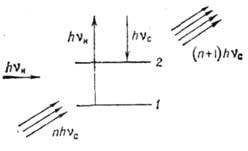
Рис. 2. Схема вынужденного
комбинационного рассеяния: 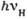 - фотон накачки;
- фотон накачки; 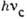 - стоксов фотон; 1 - основное состояние; 2 - возбуждённое состояние
системы.
- стоксов фотон; 1 - основное состояние; 2 - возбуждённое состояние
системы.
Это приводит к тому, что
вероятность 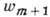 рассеяния
рассеяния
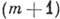 -го фотона в данную
моду (в частности, в данном направлении, рис. 2), где уже имеется т фотонов,
будет в (m+1) раз больше вероятности спонтанного рассеяния:
-го фотона в данную
моду (в частности, в данном направлении, рис. 2), где уже имеется т фотонов,
будет в (m+1) раз больше вероятности спонтанного рассеяния: 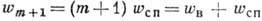 ,
где
,
где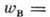
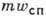 - вероятность вынужденного рассеяния света в данную моду. T. к. m ~ Iс, где Iс-интенсивность
рассеянного в данную моду света, и
- вероятность вынужденного рассеяния света в данную моду. T. к. m ~ Iс, где Iс-интенсивность
рассеянного в данную моду света, и  ,
то
,
то  ~Iс*Iн,
т. е. вероятность вынужденного рассеяния света пропорциональна произведению интенсивностей накачки
(Iн) и рассеянного света (IС). Учитывая,
что можно показать, что при
~Iс*Iн,
т. е. вероятность вынужденного рассеяния света пропорциональна произведению интенсивностей накачки
(Iн) и рассеянного света (IС). Учитывая,
что можно показать, что при 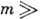 1 для стационарного случая (т. е. при
1 для стационарного случая (т. е. при 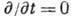 )
имеет место уравнение
)
имеет место уравнение 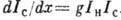 , описывающее экспоненциальное усиление рассеянного света, как и при классическом
рассмотрении.
, описывающее экспоненциальное усиление рассеянного света, как и при классическом
рассмотрении.
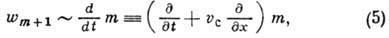
Каждому виду спонтанного рассеяния можно сопоставить соответствующее
вынужденное рассеяние света. Поэтому классификация вынужденного рассеяния света
аналогична классификации видов спонтанного рассеяния.
По причинам историч. характера рассеяние, определяемое квантовыми микросистемами
(молекулами, атомами, электронами), наз. комбинационным, а рассеяние, определяемое
макроскопич. флуктуациями среды (плотности, температуры и др. термодинамич. параметров),
а также ориентацией молекул в газах, твёрдых телах, жидкостях, наз. молекулярным.
Вынужденное комбинационное рассеяние (BKP) может быть: на колебат. уровнях молекул
газов, жидкостей, твёрдых тел (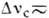 2*102
2*102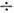 4*103
см-1; коэф. усиления g ~10-2
4*103
см-1; коэф. усиления g ~10-2 10-3
см/МВт; спектральный диапазон лазеров - источников накачки
10-3
см/МВт; спектральный диапазон лазеров - источников накачки 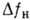 - от УФ до средних ИК); на вращат. уровнях молекул газов (
- от УФ до средних ИК); на вращат. уровнях молекул газов (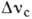 =(1
=(1 6)*102
см-1; g~10-3
6)*102
см-1; g~10-3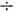 10-4
см/МВт;
10-4
см/МВт; 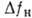 - ближний
и средний ИК); на электронных уровнях атомов атомарных газов (пары металлов)
(
- ближний
и средний ИК); на электронных уровнях атомов атомарных газов (пары металлов)
(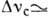 104
см-1, g~10-2 см/МВт;
104
см-1, g~10-2 см/МВт; 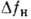 -
от УФ до видимого); на спиновых подуровнях уровней полупроводников, связанное
с переворачиванием спина электрона в магн. поле (
-
от УФ до видимого); на спиновых подуровнях уровней полупроводников, связанное
с переворачиванием спина электрона в магн. поле (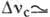 10
10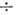 200
см-1, регулируется магн. полем,
200
см-1, регулируется магн. полем, 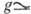 103
103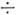 10-1см/МВт;
10-1см/МВт;
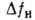 - средний ИК: 5,
10, 12 мкм); BKP на поляритонах в ионных кристаллах t
- средний ИК: 5,
10, 12 мкм); BKP на поляритонах в ионных кристаллах t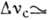 (1
(1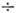 5)*102
см-1, регулируется поворотом кристалла, g=10-2 см/МВт;
5)*102
см-1, регулируется поворотом кристалла, g=10-2 см/МВт;
 - видимый]. К молекулярному
вынужденному рассеянию относятся: вынужденное рассеяние Мандельштама - Бриллюэна
(BPMB), происходящее на гиперзвуковых волнах в газах, жидкостях, твёрдых телах,
плазме [
- видимый]. К молекулярному
вынужденному рассеянию относятся: вынужденное рассеяние Мандельштама - Бриллюэна
(BPMB), происходящее на гиперзвуковых волнах в газах, жидкостях, твёрдых телах,
плазме [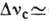 (1
(1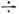 10)*10-2
см-1, g=10-1
10)*10-2
см-1, g=10-1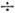 10-2
см/МВт;
10-2
см/МВт; 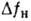 -от видимого
до ближнего ИК]; вынужденное рассеяние крыла линии Рэлея (BPKP), связанное с
анизотропией молекул жидкостей и газов (
-от видимого
до ближнего ИК]; вынужденное рассеяние крыла линии Рэлея (BPKP), связанное с
анизотропией молекул жидкостей и газов (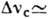 1
1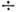 102
см-1;
102
см-1; 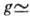 10-3
см/МВт;
10-3
см/МВт; 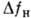 -
видимый); вынужденное температурное рассеяние (BTP) на температурных волках, обусловленное поглощением света (BTP-1) или электрокалорическим эффектом (ВТР-2) в жидкостях и газах (
-
видимый); вынужденное температурное рассеяние (BTP) на температурных волках, обусловленное поглощением света (BTP-1) или электрокалорическим эффектом (ВТР-2) в жидкостях и газах (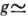 10-3
см/МВт,
10-3
см/МВт, 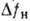 - видимый);
вынужденное концентрационное рассеяние на волнах концентрации в смесях разл.
жидкостей или газов (
- видимый);
вынужденное концентрационное рассеяние на волнах концентрации в смесях разл.
жидкостей или газов (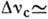 1
1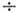 10
см-1;
10
см-1; 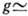 10-3 см/МВт;
10-3 см/МВт; 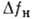 - видимый). Выражение коэф. усиления g через измеряемые величины зависит
от вида вынужденного рассеяния света. Так, напр., для BKP
- видимый). Выражение коэф. усиления g через измеряемые величины зависит
от вида вынужденного рассеяния света. Так, напр., для BKP
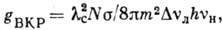
где 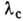 -
длина волны стоксовой компоненты, N (см-3) - разность населённостей
осн. и возбуждённого уровней. Для ВРМБ
-
длина волны стоксовой компоненты, N (см-3) - разность населённостей
осн. и возбуждённого уровней. Для ВРМБ
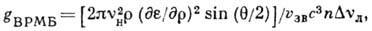
где 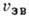 - скорость звука, п - показатель преломления среды,
- скорость звука, п - показатель преломления среды, 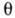 - угол рассеяния (рассеяние назад соответствует
- угол рассеяния (рассеяние назад соответствует 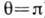 ),
), 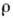 - плотность
среды,
- плотность
среды, 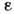 - её диэлектрич.
проницаемость.
- её диэлектрич.
проницаемость.
Усиление рассеянного света
происходит до тех пор, пока можно пренебречь эффектами насыщения. Преобразование
излучения накачки в стоксовы и антистоксовы компоненты уменьшает мощность (и
энергию) накачки, а следовательно, и её интенсивность, что приводит к уменьшению
усиления (т.н. насыщение по накачке).
К уменьшению коэф. усиления приводит также выравнивание населённости верх. и ниж. рабочих уровней (рис. 2), к-рое происходит, если объёмная скорость преобразования фотонов накачки велика по сравнению со скоростью релаксации в среде (т. н. насыщение среды).
Вынужденное рассеяние света, в отличие от спонтанного, даёт возможность достичь высокой степени когерентности рассеянного света, т. к. состояние рассеянного фотона уже задаётся фотоном, содержащимся в определ. моде. Это означает, что излучение любого центра рассеяния находится в фазе с уже имеющимся рассеянным светом. В этом смысле вынужденного рассеяния света аналогично вынужденному излучению при резонансном взаимодействии излучения с атомами и молекулами. Точно так же степень когерентности при вынужденном рассеянии света во много раз выше степени когерентности спонтанно рассеянного света.
Большой диапазон ширин
линий, разнообразные возможности концентрации световой энергии в разл. средах
приводят к тому, что вынужденное рассеяние света наблюдается не только
в поле мощных импульсов одномодовых лазеров, но и в поле лазеров непрерывного
действия, возбуждающем вынужденном рассеянии света в волоконных световодах. BKP в волоконных световодах
может наблюдаться при мощности накачки 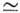 0
1 Вт; спектр BKP в кварцевых стёклах широк, и с помощью дисперсионного элемента
можно осуществлять перестройку частоты ~300 см-1. Поэтому на основе
BKP в волоконных световодах созданы перестраиваемые в ближней ИК-области спектра
волоконные генераторы лазерного излучения.
0
1 Вт; спектр BKP в кварцевых стёклах широк, и с помощью дисперсионного элемента
можно осуществлять перестройку частоты ~300 см-1. Поэтому на основе
BKP в волоконных световодах созданы перестраиваемые в ближней ИК-области спектра
волоконные генераторы лазерного излучения.
Интересные физ. и прикладные
возможности связаны с вынужденным рассеянием света пикосекундных лазерных импульсов - нестационарным
BKP, возникающим в условиях, когда длительность импульса сравнима с временем
релаксации фазы элементарного возбуждения, ответственного за рассеяние [5].
В этих случаях часто возникают эффекты инерц. запаздывания, сужения стоксова
импульса и др.
Вынужденное рассеяние света наблюдается и при "шумовой" накачке - оптич.
излучении, обладающем низкой пространственной
и временной когерентностью [6]. В этом случае вынужденного рассеяния света может быть использовано
для повышения степени когерентности.
Вынужденное рассеяние света нашло широкое
практич. применение в комбинационных лазерах для эффективного преобразования
частоты лазерного излучения; в активной лазерной спектроскопии, позволяющей
проводить количеств. и качеств. газовый анализ, локальную диагностику параметров
плазмы и т. п.; в задачах по обращению волнового фронта.

А. 3. Грасюк
|
|