Глоссарий по физике

Ферромагнитный резонанс

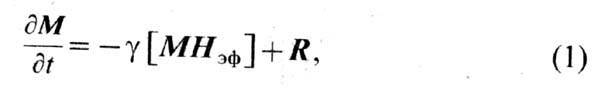
Ферромагнитный резонанс - резонансное поглощение эл--магн. энергии ферромагнетиком, один из видов электронного магнитного резонанса в твёрдом теле. От электронного парамагнитного резонанса (ЭПР) Ф. р. отличается тем, что поглощение энергии при Ф. р. на много порядков сильнее и условие резонанса (связь между резонансной частотой перем. поля и величиной пост. магн. поля) существенно зависит от формы образцов. Эти отличия вызваны тем, что Ф. р. является коллективным эффектом: элементарные магн. моменты ферромагнетика сильно связаны и поглощение энергии происходит в результате взаимодействия перем. поля с суммарными магн. моментами макроскопич. объёмов вещества. Поэтому описание Ф. р. возможно в рамках классич. макроскопич. теории. Термин "Ф. р." иногда распространяют и на магн. резонанс в ферримагнетиках, поскольку теория Ф. р. применима к одному из типов колебаний намагниченности в ферримагнетиках. Однако резонанс в ферримагнетиках имеет ряд особенностей (см. Ферримагнитный резонанс ).Однородные колебания намагниченности, происходящие при Ф. р., могут рассматриваться как предельный случай элементарных возбуждений магн. системы ферромагнетика- спиновых волн при волновом числе k->0.

Ф. р. предсказал в 1912 В. К. Аркадьев исходя из классических, а в 1923 Я. Г. Дорфман исходя из квантовых соображений. Важный вклад в эту теорию внёс Ч. Киттель (С. Kittel, 1948), выяснивший влияние на условие Ф. р. формы образца и магн. анизотропии. Экспериментально Ф. р. в металлах обнаружил Дж. Гриффите (J. Н. К. Griffiths, 1946), в ферритах - У. Хьюитт (W. Н. Hewitt, 1949). Установки (спектрометры) для экспе-рим. исследования Ф. р. включают в себя генератор СВЧ, резонатор или волновод с исследуемым образцом, детектор с системой индикации и магн. систему. Они принципиально не отличаются от спектрометров ЭПР. Но при исследовании Ф. р., в отличие от ЭПР, обычно не требуется (кроме случая тонких плёнок или проволок) высокой чувствительности, а возникает проблема правильного перехода от непосредственно измеряемых коэф. прохождения или отражения к компонентам тензора динамич. магн. восприимчивости (см. Магнитная проницаемость).

Динамическая магнитная восприимчивость. Ур-ние движения намагниченности М ферромагнетика имеет вид:

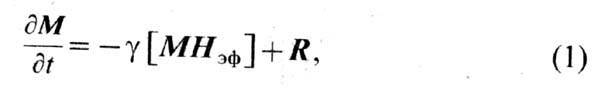
где t - время; 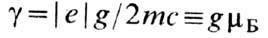-магнитомеханическое отношение (е - заряд электрона, т - его масса покоя, с- скорость света, g-фактор спектроскопического расщепления,. m_B- магнетон Бора); H_эф - эфф. поле; R - дис-сипативн. член, учитывающий потери энергии. Если намагниченность обусловлена только спиновыми моментами электронов, то g = 2,0023 и g= 1,7609•10⁷ Э^-1с^-1. Эффективное поле

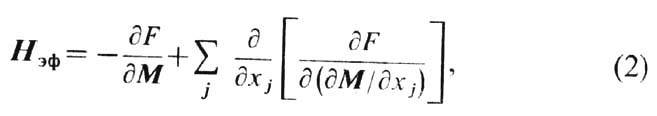
где x_j-декартовы координаты (j= 1, 2, 3); F-плотность свободной энергии (в дальнейшем будем называть её энергией), включающая магн. энергию (во внеш. поле и внутреннюю) и энергии взаимодействия магн. подсистемы ферромагнетика со всеми др. подсистемами. Классич. теория Ф. р. основывается на решении ур-ния (1) совместно с ур-ниями классич. электродинамики с учётом граничных условий на всех поверхностях раздела сред, входящих в рассматриваемую систему.

Динамич. магн. восприимчивость ферромагнетика может быть найдена в результате решения ур-ния (1) при заданных постоянном Н₀ и переменном h_~ магн. полях в каждой точке; при этом в учёте ур-ний электродинамики и граничных условий нет необходимости. Сделаем следующие допущения: 1) намагниченность однородна; тогда в правой части ур-ния (2) нужно принимать во внимание только первый член; 2) ферромагнетик изотропный и непроводящий, магнитоупругое взаимодействие не учитывается; тогда в F входят только магн. энергия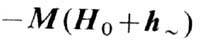 и обменная энергия, к-рую при однородной намагниченности можно записать в виде 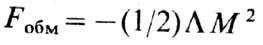где L- константа обменного взаимодействия; эфф. поле обменного взаимодействия в ур-ние (1) не войдёт и, т. о., 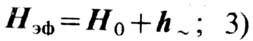потери энергии не учитываются, т. е. R = 0; 4) рассматривается случай малых амплитуд, т. е.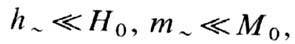 где M₀-постоянная, т_~-переменная составляющие М.

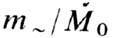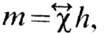Решая ур-ние (1) при этих допущениях методом после-доват. приближений, в нулевом приближении по малым величинам иполучим [М₀H₀ ] = 0 (в общем случае было бы [М₀H_эф0 ] = 0). В первом приближении, принимая гармонич. зависимость от времени (h_~=hexpiwt, m_~ = mexpiwt), получим линеаризов. ур-ние движения для комплексных амплитуд h и т, решение к-рого имеет вид где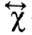-тензор динамич. магн. восприимчивости:

здесь .

а 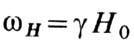. Как видно из выражений (3) и (4), тензор 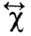обладает антисимметричными недиагональными компонентами 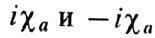и характеризуется резонансной зависимостью всех компонент от частоты и пост. поля (рис. 1). Первое свойство приводит к ряду т.н. н е в з а и м н ы х э ф ф е к т о в в системах, содержащих намагниченные фер-ромагн. образцы, в частности к Фарадея эффекту ,а второе свойство обусловливает Ф. р.

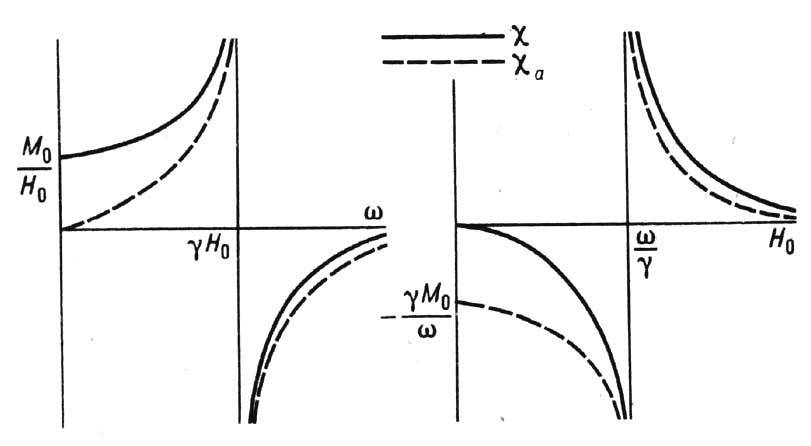
Рис. 1. Частотные и полевые зависимости компонент тензора магнитной ВЧ-восприимчивости, намагниченного до насыщения изо-тропного ферромагнетика (без учёта потерь).

Для учёта потерь энергии следует решать ур-ние (1) с диссипативным членом R; он записывается обычно в одной из следующих форм: в форме:

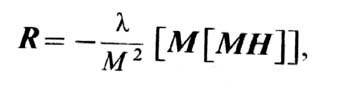
в форме Гильберта:

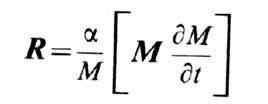
или в форме Блоха - Бломбергена:

где c₀=M₀/H₀ В рассматриваемом линейном приближении и при малых потерях эти формы эквивалентны и входящие в них параметры диссипации связаны соотношениями 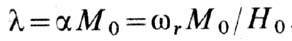. С учётом потерь компоненты становятся комплексными, их вещественные части c' и c_a' проходят через нуль, а мнимые c'' и c_a'' -через максимум вблизи w=w_H . В этой точке

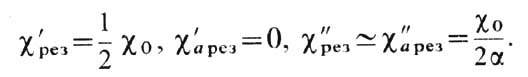
Частотные зависимости компонент тензора магн. проницаемости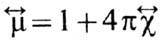 приведены на рис. 2.

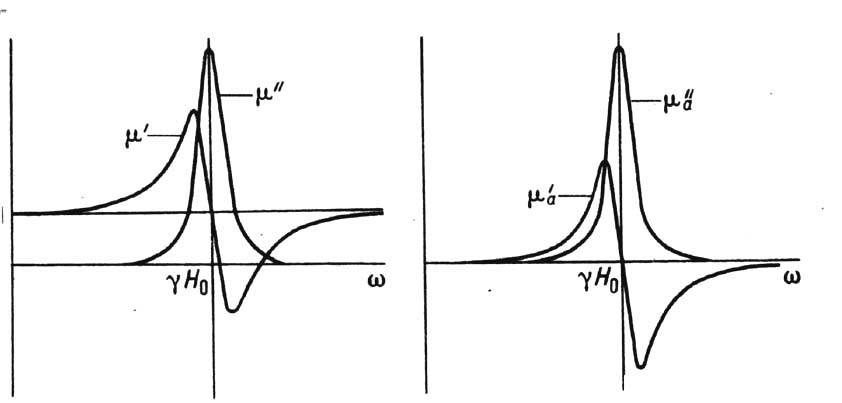
Рис. 2. Частотные зависимости компонент тензора магнитной ВЧ-проницаемости намагниченного до насыщения изотропного ферромагнетика.

Ферромагнитный резонанс в малом эллипсоиде. Для описания Ф. р. в конкретных системах, содержащих ферро-магн. образцы, необходимо решать граничные эл--дина-мич. задачи при соответствующих значениях компонент

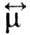и диэлектрич. проницаемости Простейшей из таких задач является задача о Ф. р. в малом (по сравнению с длиной эл--магн. волны) эллипсоиде, находящемся в заданных внеш. полях: постоянном Н_е0 и переменном с комплексной амплитудой h_e. Малость образца позволяет ограничиться магнитостатич. приближением, т. е. пренебречь в ур-ниях Максвелла членами (1/с) 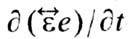и 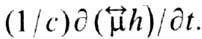Тогда внутр. поле Н и намагниченность М в ферромагн. эллипсоиде однородны и связаны с внеш. полем Н_е соотношением

где -симметричный тензор размагничивания. В осях координат, совпадающих с осями эллипсоида, он становится диагональным, и его компоненты наз. размагничивающими факторами; их сумма 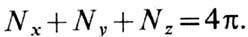Выражения (5) справедливы для постоянных и переменных составляющих. Подставляя их в линеаризов. ур-ние движения, мы получим зависимость т от внеш. поля: 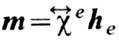, где-внеш. динамич. восприимчивость. Тензор , как и 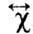, несимметричен; в отличие от 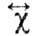, он характеризует не вещество, а образец (точнее, малый эллипсоид) из этого вещества.

Без учёта потерь компоненты имеют полюса при частоте

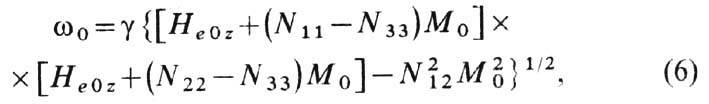
где N_ij(i, j=1, 2, 3) - компоненты тензора в системе координат, в к-рой третья ось (ось z) совпадает с направлением М₀, a H_e0z - проекция Н_е0 на эту ось. Если Н_e0 направлено по одной из осей эллипсоида, то

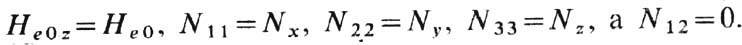
Ф-ла (6) переходит при этом в ф о р м у л у К и т т е л я; её частные случаи приведены в табл. Для сферы зависимость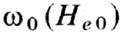 является наиб. простой и не содержит М₀. Поэтому образцы в виде сферы наиб. широко используются при экспе-рим. исследованиях Ф. р.

При нек-рых условиях в малых образцах возможно возбуждение также неоднородных колебаний намагниченности, напр. уокеровских колебаний в эллипсоидах вращения, в частности в сферах и дисках.

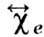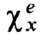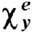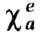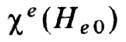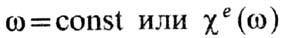С учётом потерь компоненты -диагональные и и антисимметричные -становятся комплексными, их мнимые части имеют максимумы вблизи частоты, определяемой ур-нием (6), к-рая и является частотой Ф. р. в малом эллипсоиде. Ширины DН и Dw резонансных кривых [соответственно при при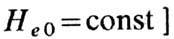пропорц. параметрам диссипации l,a или w_r , а макс. значения этих кривых обратно пропорц. им. При малых потерях 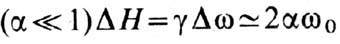, и в частном случае эллипсоида вращения

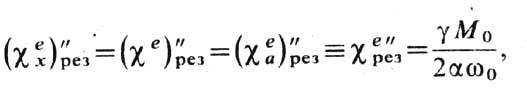
так что имеет место соотношение

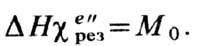
Намагниченный ферромагн. эллипсоид вблизи резонансной частоты может рассматриваться как колебат. система с добротностью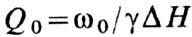 ; в случае эллипсоида вращения 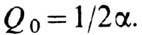В образцах из высококачеств. монокристаллов ферро- или ферримагнетиков величины DH малы и добротности достигают больших значений. Напр., для феррита Y₃Fe₅O₁₂ со структурой граната (ЖИГ) в трёх-сантиметровом диапазоне

Влияние кристаллографич. магнитной анизотропии на Ф. р. может быть учтено, если к величине H_эф в ур-нии (3) добавить, согласно ур-нию (2), эфф. поле анизотропии:

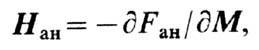
где F_ан - энергия кристаллографич. магн. анизотропии. В случае монокристаллич. образца это приводит к зависимости резонансной частоты или резонансного поля от углов, к-рые образует вектор М₀ с осями кристаллич. решётки образца. Пример такой зависимости приведён на рис. 3; поле H_рез максимально при ориентации М₀ по оси <100>, являющейся в данном случае осью трудного намагничивания, и минимально, когда М₀ направлена вдоль оси лёгкого намагничивания.

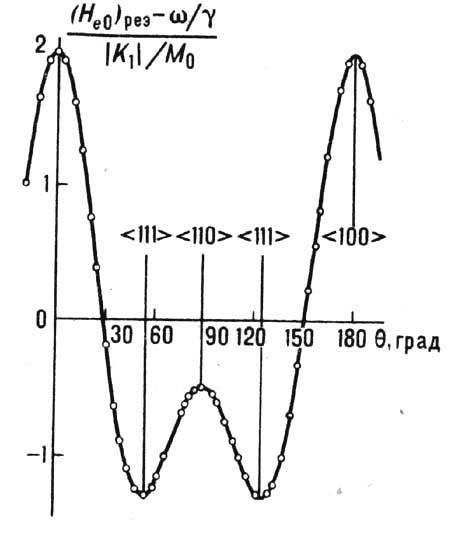
Рис. 3. Угловая зависимость резонансного поля для кубического монокристалла с первой константой анизотропии K₁<0. q - угол между внешним постоянным магнитным полем и осью <100> в плоскости {110}. Точки - эксперимент для сферы из Y₃Fe₅O₁₂ на частоте 9,3 Гц при комнатной температуре; линия -расчёт при

В поликристаллич. образцах разброс направлений кристаллографич. осей в разл. зёрнах приводит к уширению DН_ан и сдвигу резонансных кривых по отношению к резонансным кривым изотропных образцов. В предельном случае |K₁|/M₀>>4pM₀ (где К₁-первая константа анизотропии), когда колебания намагниченности в разл. зёрнах можно считать независимыми, DН_ан оказывается ~2|K₁|/M₀ . Однако для большинства поликристаллич. магн. материалов, используемых в технике СВЧ, выполняется обратное неравенство, и магн. взаимодействие переменных намагниченностей зёрен приводит к существенному уменьшению DН_ан.

На Ф. р. оказывает также влияние магнитоупругая анизотропия, обусловленная упругими напряжениями, спонтанными или внешними. Внеш. напряжения приводят к сдвигу резонансных кривых, зависящему от магнитоуп-ругих постоянных веществ. Неоднородные упругие напряжения, в частности вызванные дислокациями, приводят к расширению резонансных кривых. Заметный вклад в DН поликристаллов вносит пористость.

Процессы релаксации при ферромагнитном резонансе, к-рые феноменологически учитываются параметрами диссипации l,a или w_r и определяют величины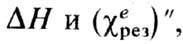 могут быть подразделены на спин-спиновые и спин-решёточные. Первые осуществляют передачу энергии от непосредственно возбуждаемого при Ф. р. однородного типа колебаний другим, неоднородным колебаниям магн. (спиновой) системы ферромагнетика - спиновым волнам. Вторые приводят к передаче энергии от магн. системы кри-сталлич. решётке, причём эта передача может происходить непосредственно (прямая спин-решёточная релаксация) или через др. подсистемы (косвенная спин-решёточная релаксация). Спин-спиновые процессы, в свою очередь, делятся на собственные (к-рые могут протекать и в идеальном кристалле) и несобственные (обусловленные дефектами).

Для описания процессов релаксации при Ф. р. необходимо использовать квантовые представления. Собственные процессы спин-спиновой релаксации трактуются при этом как процессы рождения и уничтожения квазичастиц-магнонов ,обусловленные высшими, неквадратичными членами гамильтониана идеального ферромагнетика в представлении вторичного квантования. Наиб. роль играют, вообще говоря, трёхмагнонные процессы слияния и расщепления, вызванные магн. взаимодействием, и четы-рёхмагнонные процессы рассеяния, обусловленные обменным взаимодействием (рис. 4). Однако в случае релаксации однородных колебаний намагниченности, возбуждаемых при Ф. р., процессы трёхмагнонного слияния и четырёх-магнонного рассеяния запрещены законами сохранения энергии и квазиимпульса магнонов. Процесс трёхмагнонного расщепления в ферромагнетике разрешён лишь при низких частотах, в случае сферич. образцов - при 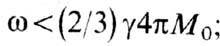вклад его в DН не превышает ~0,1 Э. Пренебрежимо малым является вклад в DН (для однородных магн. колебаний) и процессов прямой спин-решёточной релаксации. Сравнительно большие величины DН, к-рые наблюдаются в поликристаллич. ферритах и несовершенных образцах монокристаллов, обусловлены несобственными процессами спин-спиновой релаксации и косвенными спин-решёточными процессами.

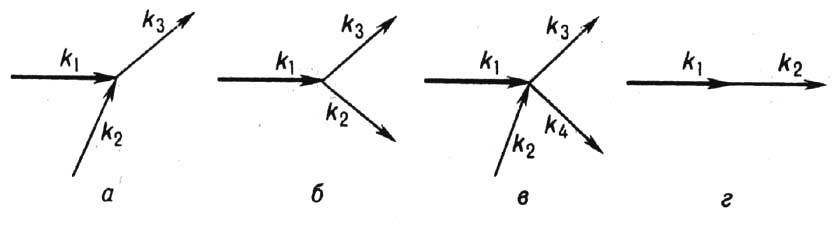
Рис. 4. Элементарные процессы, лежащие в основе процессов релаксации при ферромагнитном резонансе: а-трёхмагнонных процессов слияния; 6 - трёхмагнонных процессов расщепления; в - че-тырёхмагнонных процессов рассеяния; г -двухмагнонных процессов (в неидеальном кристалле); k₁-волновой вектор магноной; релаксация которых рассматривается.

В неидеальных кристаллах закон сохранения квазиимпульса может не выполняться при элементарных процессах превращения магнонов, и поэтому могут происходить несобственные двухмагнонные процессы уничтожения маг-нона однородных колебаний и рождения вырожденного с ним (имеющего ту же частоту) магнона с 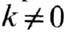(рис. 4). Такие процессы можно назвать процессами рассеяния маг-нонов на неоднородностях. Неоднородностями могут являться: "химические" неоднородности - флуктуации распределения ионов по узлам кристалла; упоминавшиеся выше вариации направлений кристаллографич. осей в по- ликристаллах; неоднородные упругие напряжения; "геометрические" неоднородности - поры и шероховатости поверхности образцов. Последний вид неоднородностей играет большую роль в случае образцов из совершенных монокристаллов; получение упоминавшихся выше малых значений DН требует тщательной полировки поверхности образцов.

Среди процессов косвенной спин-решёточной релаксации наиб. роль играют процессы, связанные с носителями заряда (см. ниже), и процессы, обусловленные ионами с сильным спин-орбитальным взаимодействием и высокой частотой собственной релаксации. К таким ионам относятся редкоземельные ионы, присутствующие в виде малых примесей в ЖИГ, и ионы Fe²⁺ и Fe⁴⁺ , к-рые возникают в ЖИГ и др. ферритах вследствие образования вакансий или замещения части основных ионов Fe³⁺ ионами с др. валентностью. Характерными чертами влияния таких ионов на Ф. р. являются максимумы Н_рез при нек-рых углах между М₀ и осями кристалла и температурные максимумы DН, к-рые возникают при таких темп-pax (обычно в интервале 10-100 К), когда частота релаксации ионов становится равной частоте колебаний w.

Ф. р. в эллипсоидальных (в частности, сферических) образцах с размерами, превышающими такие, при к-рых хорошо применимо магнитостатич. приближение, иногда наз. м а г н и т о д и н а м и ч е с к и м р е з о н а н с о м. Его можно трактовать (рис. 5) как результат связи между магнитостатич. колебаниями (частота к-рых не зависит от размера и-в случае сферы - пропорциональна H_e0)и эл--магн. колебаниями образца с m=1 (частота к-рых обратно пропорц. размерам и не зависит от Н_е0). Для образцов ещё больших размеров и неэллипсоидальной формы, напр. для ферритовых образцов в волноводах, к-рые используются в ферритовых СВЧ-устройствах, такая трактовка неприменима и необходимо решение соответствующих граничных эл--динамич. задач.

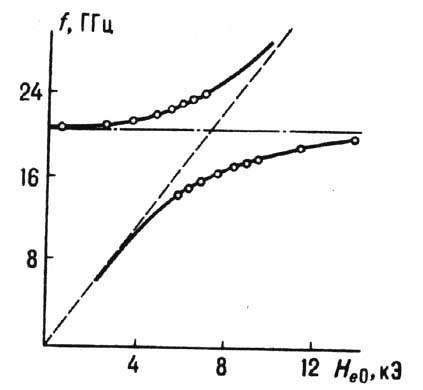
Рис. 5. Зависимость частоты ферромагнитного резонанса в сфере большого (3,72 мм) диаметра от внешнего постоянного магнитного поля. Штриховая линия -"киттелевская" частота 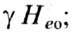штрих-пунктир - частота электромагнитных колебаний сферы с m=1; кружки-эксперимент на частоте 9,3 ГГц.

Ф. р. может наблюдаться и в ненасыщенных образцах при наличии ферромагнитных доменов. Если доменная структура является регулярной, т. е. имеется неск. групп доменов с разл. ориентациями пост. намагниченности, напр. две группы с М₁₀ и М₂₀, то происходят связанные колебания намагниченности в этих группах и число резонансных частот или полей равно числу групп доменов. Для наблюдения такого резонанса в нек-ром интервале значений поля Н_е0 необходимо, чтобы это поле не приводило к смещению границ доменов. Доменная структура и частоты Ф. р. для одного из случаев, когда это условие выполняется, приведены на рис. 6. Тип колебаний с частотой w₁ возбуждается перем. магн. полем, перпендикулярным пост. полю Н_е0, а тип колебаний с частотой w_||-перем. полем, параллельным Н_е0.

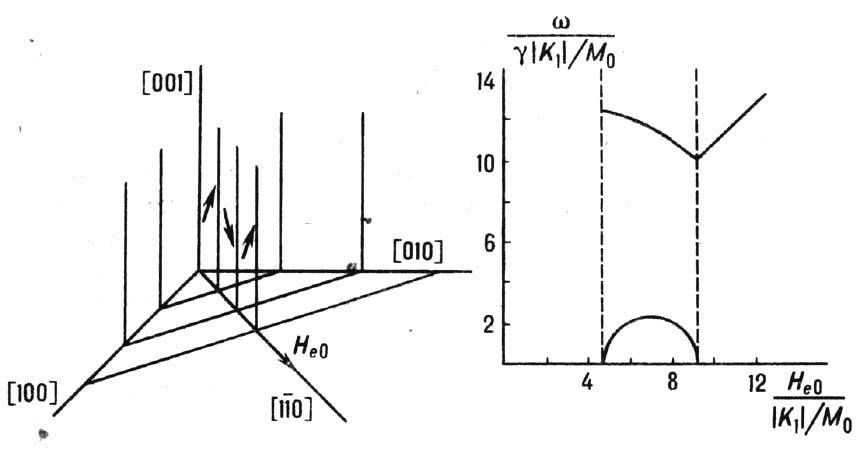
Рис. 6. Доменная структура и частоты ферромагнитного резонанса в малой сфере из кубического ферромагнетика при К₁<0 (K₁-первая константа анизотропии).

При нерегулярной доменной структуре, к-рая, как правило, имеет место в поликристаллич. образцах, разброс ориентации М₀, размеров и формы доменов приводит к значит. уширению резонансных кривых. В отсутствие внеш. пост. поля поглощение эл--магн. энергии (т. н. е с т е с т в е н н ы й Ф. р.) происходит в широком интервале частот:

При рассмотрении влияния носителей заряда на Ф. р. представляют интерес два предельных случая: d>>d и d<<d, где d-наим. размер образца (для плёнки-её толщина, для сферы-диаметр), d - глубина проникновения эл--магн. поля в вещество (толщина скин-слоя, см. Скин-эффект ).В первом случае, к-рый обычно реализуется в ферритах, электропроводность приводит к джоулевым потерям, обусловленным вихревыми токами, к-рые наводятся перем. намагниченностью. В частности, для сферы обусловленное этим эффектом уширение резонансной кривой

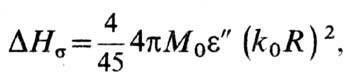
где e'' =4ps/w, s - уд. проводимость, k₀ = w/c, a R-радиус сферы. Оценка показывает, что в трёхсантиметровом диапазоне этот вклад в DH становится существенным

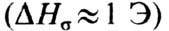при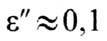 и радиусе сферы R=1 мм. В ферритах, электропроводность к-рых носит характер термоактивированных перескоков электронов между раз-новалентными ионами, напр. Fe²⁺ и Fe³⁺ , существует и др. источник магн. потерь при Ф. р., связанный с электропроводностью. Он похож на упомянутый выше процесс косвенной спин-решёточной релаксации, обусловленный ионами с сильной спин-орбитальной связью. Отличие заключается лишь в том, что теперь под действием колебаний намагниченности происходят не внутриионные, а межионные переходы электронов; вследствие больших времён релаксации, связанных с этими переходами, температурные максимумы DН лежат теперь при более высоких температурах.

В другом предельном случае (d << d), характерном для металлов, колебания намагниченности при Ф. р. являются неоднородными, их амплитуды экспоненциально убывают по мере удаления от поверхности ферромагн. металла. В грубом приближении можно считать, что колебания однородны, но происходят только в поверхностном слое толщиной d. Тогда для расчёта условий резонанса можно использовать ф-лу (6), помня, однако, что входящая в неё величина N₃₃ представляет собой размагничивающий фактор для пост. полей, а остальные компоненты тензора размагничивания суть эфф. размагничивающие факторы для тонкой плёнки, прилегающей к поверхности образца.

В действительности при Ф. р. в металле на его поверхности возбуждаются спиновые волны, к-рые распространяются в глубь металла и затухают, в осн., на длине d вследствие магн. потерь и электрич. потерь, обусловленных проводимостью металла. Теория этого процесса должна учитывать влияние обменного взаимодействия на параметры всех 4 типов волн, к-рые могут распространяться в ферромагн. металле, а также дополнит. (обменные) граничные условия на поверхности металла. В результате может быть вычислен поверхностный импеданс металла Z_S и найдена ширина резонансной линии DH, к-рая в данном случае определяется, как ширина кривой Z_S²' (H₀) на половине её высоты. Сравнение результатов таких расчётов с экспериментом позволяет найти вклад DH_маг магн. потерь, пропорциональный параметру диссипации и вклад DH_обм, обусловленный проводимостью и обменным взаимодействием. В случае преобладания этого вклада и нормального скин-эффекта

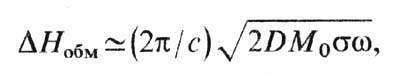
где D - постоянная неоднородного обмена (или спиновой жёсткости). Такого же порядка оказывается и сдвиг (в сторону меньших полей) H_рез. Для более точного определения вклада DH_маг может быть использовано явление антирезонанса, когда DH_обм отсутствует. Вклад DH_обм преобладает, в частности, в сантиметровом диапазоне для монокристаллов Fe, а вклад DH_маг - для монокристаллов Ni.

Применение в технике. Ф. р. часто понимается в широком смысле как совокупность явлений, происходящих в ферро- и ферримагнетиках, находящихся в постоянном (или медленно изменяющемся) магн. поле и переменном эл--магн. поле диапазона СВЧ. При таком определении Ф. р. это явление лежит в основе всех магн. (ферритовых) устройств, используемых в технике СВЧ. Если принять более узкое определение Ф. р. как совокупности явлений, происходящих вблизи резонансных значений частоты и пост. поля, то Ф. р. в поликристаллич. ферритах используется в резонансных вентилях СВЧ-диапазона, а в монокристаллах - в ферритовых СВЧ-фильтрах. Ф. р. широко применяется для измерения параметров ферро-и ферримагнетиков: констант магн. кристаллографич. анизотропии, магнитоупругих постоянных, а также (с применением несферич. образцов или уокеровских типов колебаний в сферах) пост. намагниченности.

Нелинейные явления при ферромагнитном резонансе. Ур-ние движения намагниченности (1) нелинейно, и при достаточно больших амплитудах перем. магн. поля возникают многочисл. нелинейные явления. Они подразделяются на два вида: одномодовые и обусловленные нелинейной связью между разл. типами колебаний (модами). Явления первого вида обусловлены прежде всего тем, что, как следует из ур-ния (1), длина вектора М сохраняется, т. е. конец его при колебаниях движется по поверхности сферы. При этом проекция M_z намагниченности на направление H₀ и М₀ уменьшается с ростом амплитуды колебаний. Уменьшение M_z сопровождается уменьшением компонент тензора магн. восприимчивости, т. е. н а с ы щ е н и е м Ф. р. Уменьшение М_z при Ф. р. может быть использовано для детектирования колебаний, однако чувствительность таких детекторов оказывается низкой. При отсутствии цилинд-рич. симметрии образца (геометрической или кристаллографической) относительно направления Н₀ величина М- при больших амплитудах колебаний зависит от времени, причём преобладает 2-я гармоника. Этот эффект может быть использован для создания удвоителей частоты СВЧ-диапазона.

Второй вид нелинейности - связь между разл. типами колебаний намагниченности - лежит в основе т. н. п а р ам е т р и ч е с к о г о в о з б у ж д е н и я спиновых волн. Оно приводит к "преждевременному" насыщению Ф. р. при амплитудах перем. поля, значительно меньших, чем те, при к-рых насыщение должно было бы наступить вследствие упомянутой выше одномодовой нелинейности, а также к дополнит. поглощению при величинах пост. поля, меньших, чем резонансные (рис. 7). Эти явления обнаружили в 1952 Н. Бломберген (N. Blombergen) и Р. У. Деймон (R. W. Damon); качественное их объяснение дали в 1955 Ф. У. Андерсон (P. W. Anderson) и X. Сул (Н. Suhl). Нелинейная связь однородных колебаний намагниченности и спиновых волн приводит к передаче им энергии однородных колебаний. При нек-рой пороговой амплитуде перем. намагниченности эта энергия превышает потери энергии спиновых волн и наступает нестабильный рост нек-рой пары спиновых волн с взаимнопротивоположными волновыми векторами k и -k; и суммой фаз, определяемой фазой перем. поля. Разность фаз пары остаётся случайной, так что возбуждаемые спиновые волны являются лишь частично когерентными.

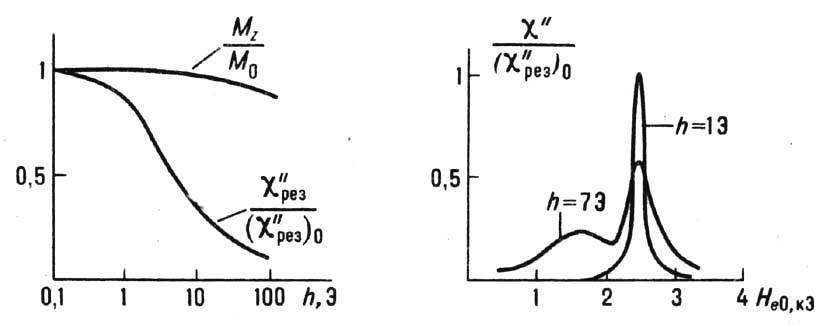
Рис. 7. Ферромагнитный резонанс при больших амплитудах переменного магнитного поля h_~

Пороговая амплитуда перем. поля h_пор оказывается наименьшей для нестабильности 1-го порядка (один магнон однородной прецессии с частотой w₀ порождает одну пару спиновых волн с частотой w_k = w₀/2) при Ф. р.:

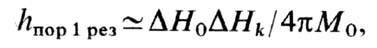
где DH₀ - ширина резонансной кривой однородных колебаний, a DH_k-спиновых волн. Для монокристаллов ЖИГ Э. Однако такой процесс разрешён законами сохранения энергии и импульса лишь при достаточно низких частотах, напр. для сферы при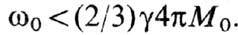 Если этот процесс при резонансе запрещён, то нестабильность 1-го порядка наступает при H₀~(0,5-0,9)H_рез и порог её оказывается на два порядка выше. В обоих случаях возбуждаются пары волн с k~10⁴см^-1 и углами между k и М₀ 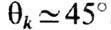. При резонансе же, если процесс 1-го порядка запрещён, имеет место нестабильность 2-го порядка- два магнона однородных колебаний возбуждают одну пару спиновых волн. Пороговое поле в этом случае

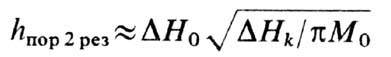
(для монокристаллов ЖИГ 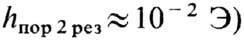, и возбуждаются пары волн с k~10⁵ см^-1 и q_k = 0.

Рассмотренные процессы аналогичны параметрич. возбуждению в контуре колебаний с частотами nw_н/2 (n= 1, 2, 3, ...) при модуляции одного из параметров контура с частотой w_н - частотой накачки (см. Параметрический резонанс ).В рассмотренном случае накачкой являлась перем. намагниченность, перпендикулярная М₀, что даёт основание называть такие процессы параметрич. возбуждением при поперечной накачке.

Параметрич. возбуждение спиновых волн может происходить, как показали в 1960 Э. Шлёман (Е. Schlomann), Дж. Грин (J. J. Green) и В. Милане (V. Milano), и при продольной (или параллельной) накачке, т. е. под действием перем. магн. поля h_z, параллельного Н₀ (линейный Ф. р. при этом не имеет места). В этом случае возбуждаются пары спиновых волн с q_k = 90° и величинами k, изменяющимися в широких пределах при изменении H₀. Пороговое поле при продольной накачке.

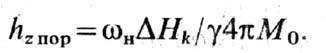
Параметрич. возбуждение спиновых волн является вредным эффектом в линейных ферритовых СВЧ-устройствах; оно ограничивает динамич. диапазон этих устройств - приводит к резкому росту потерь при превышении пороговых значений мощности на входе. Но, с др. стороны, оно используется для создания нелинейных ферритовых-СВЧ устройств: ограничителей мощности и подавителей слабых сигналов.

Литература по

1. Ферромагнитный резонанс и поведение ферромагнетиков в переменных магнитных полях. Сб. ст., под ред. С. В. Вонсов-ского, М., 1952; Ферромагнитный резонанс, под ред. С. В. Вонсов-ского, М., 1961; Моносов Я. А., Нелинейный ферромагнитный резонанс, М., 1971; Гуревич А. Г., Магнитный резонанс в ферритах и антиферромагнетиках, М., 1973; Крупичка С., Физика ферритов и родственных им магнитных окислов, пер. с нем., т. 2, М., 1976; Гуревич А. Г., Мелков Г. А., Магнитные колебания и волны, М., 1994. А. Г. Гуревич.
   к библиотеке   к оглавлению   FAQ по эфирной физике   ТОЭЭ   ТЭЦ   ТПОИ   ТИ  
   
   
   Знаете ли Вы, что только в 1990-х доплеровские измерения радиотелескопами показали скорость Маринова для CMB (космического микроволнового излучения), которую он открыл в 1974. Естественно, о Маринове никто не хотел вспоминать. Подробнее читайте в FAQ по эфирной физике.

   НОВОСТИ ФОРУМА Рыцари теории эфира

   10.11.2021 - 12:37: ПЕРСОНАЛИИ - Personalias -> WHO IS WHO - КТО ЕСТЬ КТО - Карим_Хайдаров. 10.11.2021 - 12:36: СОВЕСТЬ - Conscience -> РАСЧЕЛОВЕЧИВАНИЕ ЧЕЛОВЕКА. КОМУ ЭТО НАДО? - Карим_Хайдаров. 10.11.2021 - 12:36: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ - Upbringing, Inlightening, Education -> Просвещение от д.м.н. Александра Алексеевича Редько - Карим_Хайдаров. 10.11.2021 - 12:35: ЭКОЛОГИЯ - Ecology -> Биологическая безопасность населения - Карим_Хайдаров. 10.11.2021 - 12:34: ВОЙНА, ПОЛИТИКА И НАУКА - War, Politics and Science -> Проблема государственного терроризма - Карим_Хайдаров. 10.11.2021 - 12:34: ВОЙНА, ПОЛИТИКА И НАУКА - War, Politics and Science -> ПРАВОСУДИЯ.НЕТ - Карим_Хайдаров. 10.11.2021 - 12:34: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ - Upbringing, Inlightening, Education -> Просвещение от Вадима Глогера, США - Карим_Хайдаров. 10.11.2021 - 09:18: НОВЫЕ ТЕХНОЛОГИИ - New Technologies -> Волновая генетика Петра Гаряева, 5G-контроль и управление - Карим_Хайдаров. 10.11.2021 - 09:18: ЭКОЛОГИЯ - Ecology -> ЭКОЛОГИЯ ДЛЯ ВСЕХ - Карим_Хайдаров. 10.11.2021 - 09:16: ЭКОЛОГИЯ - Ecology -> ПРОБЛЕМЫ МЕДИЦИНЫ - Карим_Хайдаров. 10.11.2021 - 09:15: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ - Upbringing, Inlightening, Education -> Просвещение от Екатерины Коваленко - Карим_Хайдаров. 10.11.2021 - 09:13: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ - Upbringing, Inlightening, Education -> Просвещение от Вильгельма Варкентина - Карим_Хайдаров.