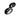 и квазиимпульс р магнона равны:
и квазиимпульс р магнона равны: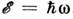 ,
,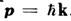 . Кристалл
с N магнитными под решетками имеет N типов (ветвей, мод)
спиновых волн с разл. законами дисперсии: ш = wi(k); i = 1, 2,
..., N.
. Кристалл
с N магнитными под решетками имеет N типов (ветвей, мод)
спиновых волн с разл. законами дисперсии: ш = wi(k); i = 1, 2,
..., N.
Спиновые волны - элементарное возбуждение магн. системы в магнитоупорядоченной среде; квазичастицы, соответствующие спиновые волны, наз. магнонами. Существование спиновых волн в ферромагнетиках предсказано Ф. Блохом (F. Bloch) в 1930. Вся совокупность экспе-рим. факторов о поведении магнитоупорядоченных тел при температуре Т значительно ниже температуры Кюри Тс (или температуры Нееля TN)свидетельствует о существовании спиновых волн (в частности, Блоха закон).
Спиновые волны, как всякая волна в кристалле, характеризуется законом дисперсии
- зависимостью её частоты w от квазиволнового вектора k. Энергия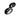 и квазиимпульс р магнона равны:
и квазиимпульс р магнона равны: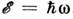 ,
,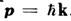 . Кристалл
с N магнитными под решетками имеет N типов (ветвей, мод)
спиновых волн с разл. законами дисперсии: ш = wi(k); i = 1, 2,
..., N.
. Кристалл
с N магнитными под решетками имеет N типов (ветвей, мод)
спиновых волн с разл. законами дисперсии: ш = wi(k); i = 1, 2,
..., N.
Классическое описание. Спиновые волны допускают наглядную классич. интерпретацию:
рассмотрим цепочку атомов, расстояние между к-рыми а, в магн. поле
Н. Если волновой вектор k = 0, то все спины синфазно прецессируют вокруг
Н с частотой w0 (однородная прецессия). При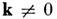 прецессия спинов неоднородна - разные спины повёрнуты на разные углы, разность
углов поворота равна ka (рис. 1). Частота неоднородной прецессии
прецессия спинов неоднородна - разные спины повёрнуты на разные углы, разность
углов поворота равна ka (рис. 1). Частота неоднородной прецессии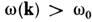 . В реальных системах малые колебания магн. моментов атомов осуществляются
в виде волн неоднородной прецессии.
. В реальных системах малые колебания магн. моментов атомов осуществляются
в виде волн неоднородной прецессии.

Рис. 1. Спиновая волна в линейной цепочке спинов: a - вид цепочки спинов в перспективе (сбоку); б - вид цепочки спинов сверху; волна изображена линией, проходящей через концы спиновых векторов.
В случае длинных волн колебания магн. моментов можно описывать как колебания
макроскопич. векторов - плотностей магн. моментов (намагниченностей)подрешёток Mi (r,t) - функций координаты r и
времени t. При неоднородной прецессии длины векторов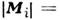
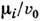 ,
где
,
где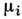 -
магн. момент атома i-й подрешётки, v0 - объём
ячейки кристалла, сохраняются;
-
магн. момент атома i-й подрешётки, v0 - объём
ячейки кристалла, сохраняются;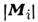 - интегралы движения. Законы дисперсии длинноволновых спиновых волн определяются
из квантового уравнения:
- интегралы движения. Законы дисперсии длинноволновых спиновых волн определяются
из квантового уравнения:
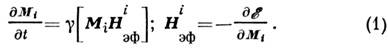
Здесь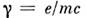 - магнитомеханическое отношение (без учёта спин-орбитальной связи);
е, т - заряд и масса электрона,
- магнитомеханическое отношение (без учёта спин-орбитальной связи);
е, т - заряд и масса электрона,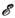 - энергия взаимодействия магн. моментов подрешёток, Нэф
- эфф. магн. поле (см. ниже). Осн. состояние определяется условием коллинеарности
намагниченностей Mi0 и эфф. магн. полей
- энергия взаимодействия магн. моментов подрешёток, Нэф
- эфф. магн. поле (см. ниже). Осн. состояние определяется условием коллинеарности
намагниченностей Mi0 и эфф. магн. полей :
:

Линеаризация ур-ния (1) с учётом (2) приводит к системе ур-ний для пере.м.
составляющих магн. моментов:
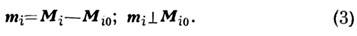
Поле Нэф, кроме пост. магн. поля Н, содержит перем. часть h - магн. поле, связанное с взаимодействием
между подрешётками и с неоднородностью их намагниченностей.
Т. к. частоты спиновых волн невелики, то для определения h можно воспользоваться
ур-ниями магнитостатики:
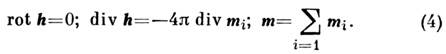
Магн. поле h осуществляет магнитодипольное взаимодействие между
колеблющимися магн. моментами. Линеаризов. ур-ния (1) совместно с (4) суть
ур-ния спиновых волн. Подставляя в них
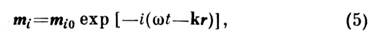
получаем алгебраич. систему ур-нии относительно амплитуд спиновых волн
mi0. Равенство нулю детерминанта этой системы приводит к ур-нию N-го порядка относительно w2.
Его решения определяют законы дисперсии спиновых волн при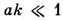
Обычно в магнитоупорядоченных средах гл. роль во взаимодействии между
магн. моментами атомов играет обменное взаимодействие ,изотропное
относительно однородного поворота магн. моментов атомов. Магн. порядок
появляется в результате спонтанного нарушения симметрии обменного
взаимодействия. Энергия обменного взаимодействия соседних атомов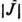 порядка температуры Кюри Тс (температуры TN); знак
J выбирается так, что при J > 0 обменное взаимодействие благоприятствовало
бы ферромагн. упорядочению, а при J < 0 - антиферромагнитному.
порядка температуры Кюри Тс (температуры TN); знак
J выбирается так, что при J > 0 обменное взаимодействие благоприятствовало
бы ферромагн. упорядочению, а при J < 0 - антиферромагнитному.
Ветви спиновых волн. Число ветвей спиновых волн равно числу магн. подрешёток.
Это обусловлено прецессионным характером движения магн. моментов подрешёток.
Ветви спиновых волн принято делить на акустические и оптические аналогично колебаниям
кристаллической решётки. Если пренебречь малыми (по сравнению с обменными),
т. н. релятивистскими, взаимодействиями (зеемановским с постоянным магн.
полем, спин-орбитальным - источником энергии магнитной анизотропии, магнитодипольным и др.), то акустич. типы спиновых волн представляют собой
голдстоуновские моды ,т. е. в их энергетич. спектре при k = 0
щель отсутствует. Частоты акустич. спиновых волн стремятся к 0 с ростом длины волны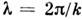 . Их число и характер закона дисперсии w(k) при
. Их число и характер закона дисперсии w(k) при зависят от структуры осн. состояния магнетика, причём при любом кол-ве
подрешёток число акустич. мод
зависят от структуры осн. состояния магнетика, причём при любом кол-ве
подрешёток число акустич. мод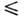 3.
У одноподрешёточного ферромагнетика одна акустич. мода с
3.
У одноподрешёточного ферромагнетика одна акустич. мода с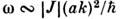 при
при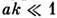 ;
у двухподрешёточного антиферромагнетика 2 вырожденные акустич. моды с
;
у двухподрешёточного антиферромагнетика 2 вырожденные акустич. моды с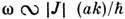 . В ферромагнетике магнон напоминает нерелятивистскую частицу с энергией
. В ферромагнетике магнон напоминает нерелятивистскую частицу с энергией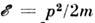 ,
в антиферромагнетике - акустич. фонон с
,
в антиферромагнетике - акустич. фонон с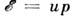 (т, и - масса частицы и скорость звука). Примеры магнетиков, имеющих
3 акустич. ветви в спектре спиновых волн, - многоподрешёточные антиферромагнетики
с неколлинеарным расположением магн. моментов в упорядоченном состоянии
при Н = 0 (UO2, CsNiCl3, CsMnBr3
и др.). Учёт релятивистских взаимодействий приводит к возникновению энергетич.
щелей в спектре акустич. ветвей спиновых волн
(т, и - масса частицы и скорость звука). Примеры магнетиков, имеющих
3 акустич. ветви в спектре спиновых волн, - многоподрешёточные антиферромагнетики
с неколлинеарным расположением магн. моментов в упорядоченном состоянии
при Н = 0 (UO2, CsNiCl3, CsMnBr3
и др.). Учёт релятивистских взаимодействий приводит к возникновению энергетич.
щелей в спектре акустич. ветвей спиновых волн  (
(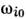 - частоты
однородной прецессии). Когда в спектре спиновых волн есть оптич. моды, их частоты
однородной прецессии
- частоты
однородной прецессии). Когда в спектре спиновых волн есть оптич. моды, их частоты
однородной прецессии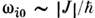
Дисперсия. спиновых волн являются причиной зависимости тензора магнитной
восприимчивости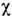 от волнового вектора
от волнового вектора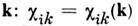 (см. Дисперсия пространственная ).Частотная дисперсия (зависимость
(см. Дисперсия пространственная ).Частотная дисперсия (зависимость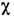 от w) является следствием прецессии магн. моментов подрешёток. Тензор
от w) является следствием прецессии магн. моментов подрешёток. Тензор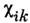 определяется в результате решения ур-ния (1), а Максвелла уравнения дают возможность найти связь между ш и k, т. е. законы дисперсии
спиновых волн, учитывающие конечность скорости света. При
определяется в результате решения ур-ния (1), а Максвелла уравнения дают возможность найти связь между ш и k, т. е. законы дисперсии
спиновых волн, учитывающие конечность скорости света. При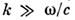 они отличаются от законов дисперсии, полученных на основе ур-ний магнитостатики
(4), малыми поправками, к-рые иногда существенны, напр. при описании
взаимодействия спиновых волн с электронами проводимости в металлах и полупроводниках.
они отличаются от законов дисперсии, полученных на основе ур-ний магнитостатики
(4), малыми поправками, к-рые иногда существенны, напр. при описании
взаимодействия спиновых волн с электронами проводимости в металлах и полупроводниках.
В магнетиках со сложной структурой (антиферромагнетиках и ферритах) изменение температуры и внеш. условий (магн. поля, давления) может привести к переориентации равновесных магн. моментов. При этом произойдёт т. н. ориентационный фазовый переход, к-рый изменит спектр спиновых волн. Если это фазовый переход 2-го рода, то он сопровождается обращением в нуль частоты одной из ветвей спиновых волн.
С ростом k (ak ~ 1) проявляется дискретная (кристаллич.) структура
магнетиков. Для получения законов дисперсии, справедливых при произвольном
значении ak, обычно используют приближённые представления спиновых
операторов через операторы рождения
через операторы рождения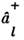 и уничтожения
и уничтожения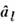 магнонов, подчиняющиеся бозевским правилам коммутации (преобразование Хольштейна
- Примакова):
магнонов, подчиняющиеся бозевским правилам коммутации (преобразование Хольштейна
- Примакова):
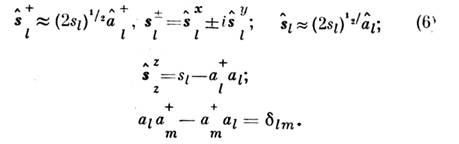
Здесь индекс I нумерует атомы, координатные оси выбраны так,
чтобы ось z для каждого атома была направлена вдоль равновесного положения
спина. Из правил коммутации для , al следует, что - любое
целое число от 0 до
до , хотя
по физич.
, хотя
по физич.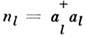 смыслу
смыслу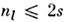 Вблизи
основного состояния ср. значение nl значительно меньше
sl и приближённые ф-лы (6) пригодны для вычисления спектра
тем точнее, чем больше sl (в квантовомеханич. пределе
Вблизи
основного состояния ср. значение nl значительно меньше
sl и приближённые ф-лы (6) пригодны для вычисления спектра
тем точнее, чем больше sl (в квантовомеханич. пределе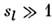 ). Однако и при sl>l ~ 1 частоты спиновых волн, как правило,
лишь небольшими поправками отличаются от значений, найденных с помощью
(6).
). Однако и при sl>l ~ 1 частоты спиновых волн, как правило,
лишь небольшими поправками отличаются от значений, найденных с помощью
(6).
Магнонный спектр. Теоретич. рассмотрение позволяет вычислить
энергию магнонов при любом k. Это приводит к периодич. зависимости
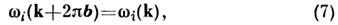
где Ь - произвольный вектор обратной решётки. Так, гамильтониан
одноподрешёточного магнетика
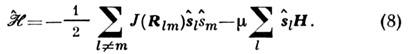
Здесь J(Rlm) - обменный интеграл между l-м и
m-м атомами, Rlm - вектор, соединяющий эти атомы,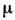 - магн. момент атома. С помощью (7) и (8) (пренебрегая взаимодействием
между магнонами) можно получить спектр магнонов:
- магн. момент атома. С помощью (7) и (8) (пренебрегая взаимодействием
между магнонами) можно получить спектр магнонов:
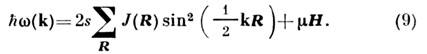
Ширина магнонной энергетич. зоны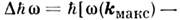 -
-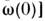 , где
, где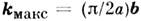 ,
равна:
,
равна:
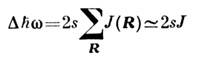
(J - обменный интеграл для ближайших соседей). Соотношение - общее свойство магнонных зон. Магнитный момент магнона. Зависимость энергии
магнона от магн. поля Н означает, что магнон обладает магн. моментом:
- общее свойство магнонных зон. Магнитный момент магнона. Зависимость энергии
магнона от магн. поля Н означает, что магнон обладает магн. моментом:

В простейшем случае чисто обменного одноподрешёточного ферромагнетика магн. момент магнона равен магн. моменту атома и направлен против равновесной намагниченности. Увеличение числа магнонов приводит к уменьшению величины спонтанной намагниченности магнетика. В многоподрешёточных магнетиках рост числа магнонов уменьшает намагниченность подрешёток.
В магн. металлах (Fe, Co, Ni и др.), где за магн. свойства ответственны
d-электроны, в формировании спектра спиновых волн принимают участие нелокализов.
электроны проводимости .В длинноволновом пределе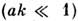 G. в. в магн. металле - одна из ветвей колебания ферми-жидкости.
G. в. в магн. металле - одна из ветвей колебания ферми-жидкости.
Газ магнонов. Магноны являются бозонами. При конечной температуре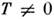 магнонов много. Их число NM пропорц. объёму тела V и растёт с ростом Т:
магнонов много. Их число NM пропорц. объёму тела V и растёт с ростом Т:
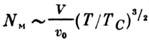
-для ферромагнетиков,

- для антиферромагнетиков.
Мн. свойства магнетиков при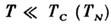 удобно описывать, считая, что спиновые волны представляют собой почти идеальный
газ магнонов (см. Вырожденный газ). Химический потенциал газа магнонов
равен 0, т. к. число магнонов не сохраняется; равновесная функция распределения
магнонов по энергиям:
удобно описывать, считая, что спиновые волны представляют собой почти идеальный
газ магнонов (см. Вырожденный газ). Химический потенциал газа магнонов
равен 0, т. к. число магнонов не сохраняется; равновесная функция распределения
магнонов по энергиям:
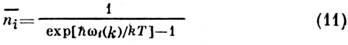
Ф-ла (11) позволяет вычислить температурную зависимость термодинамич.
характеристик магнетика (намагниченности, теплоёмкости, магн. восприимчивости
и др.). Получающиеся выражения тем точнее, чем идеальнее газ магнонов.
Неидеальность - результат взаимодействия магнонов друг с другом, с др.
квазичастицами ,(с фононами, электронами). С ростом Т число
любых квазичастиц растёт, их взаимодействие становится столь существенным,
что представление об идеальном газе магнонов перестаёт быть справедливым.
Кроме того, может нарушиться условие квазистационарности спиновых волн 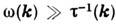 , где
, где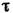 -
время жизни магнона. Поэтому простейшая концепция газа магнонов применима
при
-
время жизни магнона. Поэтому простейшая концепция газа магнонов применима
при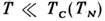 .
При этом важную роль играют низкочастотные (релятивистские) магноны; при
.
При этом важную роль играют низкочастотные (релятивистские) магноны; при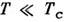 их значительно больше, чем обменных (последних экспоненциально мало). Однако
учёт изменения спектра магнонов при повышении температуры позволяет обобщить
концепцию газа магнонов практически на широкий диапазон Т, включающий
Тс.
их значительно больше, чем обменных (последних экспоненциально мало). Однако
учёт изменения спектра магнонов при повышении температуры позволяет обобщить
концепцию газа магнонов практически на широкий диапазон Т, включающий
Тс.
Влияние спиновых волн на кинетические свойства магнетиков. Спиновые волны позволяют описать не только термодинамич. (равновесные) свойства магнетиков, но и их кинетические и резонансные свойства. В теплопроводности магнетиков наряду с фононами и электронами (для проводников) принимают участие магноны: один из механизмов затухания звука - рассеяние звуковых волн на магнонах; в магн. металлах и полупроводниках рассеяние электронов на магнонах - один из механизмов электросопротивления; ферро- и антиферромагнитный резонансы можно представить как превращение фотона в магнон, при ферроакустич. резонансе в магнон превращается фонон.
Для описания кинетических и резонансных процессов существенно время
жизни магнона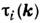 .
Среди процессов, определяющих время жизни магнонов, выделяют собств. процессы,
характерные для идеального кристалла (магнон-магнонные, магнон-фононные
и др. взаимодействия), и несобственные (рассеяние магнонов на примесях,
дислокациях, границах кристаллитов и поверхности образца).
.
Среди процессов, определяющих время жизни магнонов, выделяют собств. процессы,
характерные для идеального кристалла (магнон-магнонные, магнон-фононные
и др. взаимодействия), и несобственные (рассеяние магнонов на примесях,
дислокациях, границах кристаллитов и поверхности образца).
Взаимодействие магнонов друг с другом и с др. квазичастицами может привести
не только к их рассеянию, но и к перестройке их спектра. С возрастанием
числа магнонов (NM)наблюдается нелинейный (по NМ)
сдвиг частоты спиновой волны. Учёт членов ф-лы (8), «отброшенных» при получении ф-лы
(9), приводит к взаимодействию магнонов, носящему характер притяжения.
В результате притяжения между магнонами может образоваться своеобразный
спиновый комплекс - двухчастичное связанное состояние. В частности, в ферромагнетике,
состоящем из атомов со спином 1/2, возникает возбуждение,
соответствующее движению по кристаллу двух спинов, связанных между собой
и перевёрнутых относительно вектора намагниченности. Как правило, спиновые
комплексы образуют магноны с энергией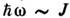 [их роль при
[их роль при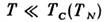 невелика].
невелика].
Резонанс между спиновой волной и волной колебания др. природы (напр., звуковой) может привести к «расталкиванию» ветвей, что проявляется в существовании гибридных колебаний, напр. магнитоупругих (см. магнитоупругие волны, магнитоупругое взаимодействие).
Экспериментальные методы. Первыми эксперим. методами исследования
спиновых волн были измерения температурной зависимости термодинамич. характеристик
- намагниченности, магн. части теплоёмкости (рис. 2, 3),
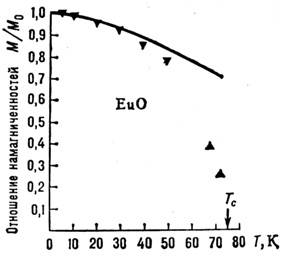
Рис. 2. Температурная зависимость намагниченности ферромагнитного
соединения ЕиО. Сплошная кривая - расчёт М(Т) по теории спиновых волн.
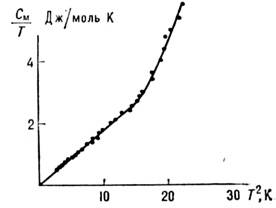
Рис. 3. Температурная зависимость магнитной части теплоёмкости См легкоплоскостного антиферромагнетика МnСО3. При низких температурах См = aТ3, резкое отклонение от этого закона происходит при Т > 6 К, соответствующей «включению» второй ветви спектра.
Неупругое рассеяние нейтронов является наиб. информативным методом,
позволяющим определить закон дисперсии спиновых волн и оценить время жизни всех
типов магнонов. Использование поляризованных нейтронов, кроме того,
даёт возможность получить сведения о поляризации
спиновых волн. Исследованы спектры
сотен магнетиков, в т. ч. сложных (рис. 4, 5).
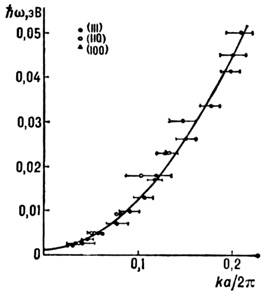
Рис. 4. Спектр спиновых волн ферромагнитного кобальтового сплава (92% Со, 8% Fе), полученных с помощью неупругого рассеяния нейтронов.
Неупругое рассеяние нейтронов не позволяет исследовать спектр
спиновых волн при предельно малых квазиволновых векторах k, т. к. в этом
случае пик неупругого рассеяния накладывается на пик упругого рассеяния
(см. Магнитная нейтронография ).Ферро- и антиферромагн. резонансы
дают возможность измерить значение частот однородной прецессии w0,
т. е. щелей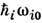 в спектре магнонов. Для исследования нач. участка спектра (
в спектре магнонов. Для исследования нач. участка спектра (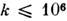 см-1) используют резонанс на стоячих спиновых волн в пластинах, параметрич.
возбуждение спиновых волн эл--магн. полем, а также неупругое рассеяние света (Мандельштама
- Бриллюэна рассеяние). Каждый из методов не универсален, но в совокупности
они позволили с большой полнотой определить спектр спиновых волн многих магнитоупорядоченных
кристаллов.
см-1) используют резонанс на стоячих спиновых волн в пластинах, параметрич.
возбуждение спиновых волн эл--магн. полем, а также неупругое рассеяние света (Мандельштама
- Бриллюэна рассеяние). Каждый из методов не универсален, но в совокупности
они позволили с большой полнотой определить спектр спиновых волн многих магнитоупорядоченных
кристаллов.
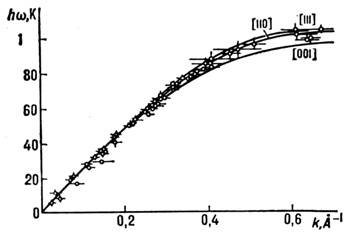
Рис. 5. Спектр спиновых волн в кубическом антиферромагнетике RbMnF3, установленный методом неупругого рассеяния нейтронов; кривые - расчёты спектров в предположении, что |J|/k = 3,4 К.

Рис. 6. Теоретический спектр спиновых волн в железоиттриевом гранате.
Длинноволновые участки спектра спиновых волн нек-рых веществ: 1)
одноподрешёточный кубич. ферромагнетик (N = 1)
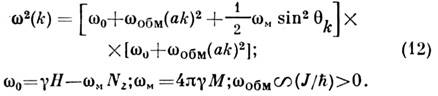
Здесь М - намагниченность насыщения, Nz - размагничивающий
фактор, - угол между намагниченностью М и волновым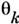 вектором k спиновой волны. Коэф. wобм
характеризует роль обменного взаимодействия магн. атомов, коэф. wм - магнитодипольного
взаимодействия. Ф-ла (12) описывает также акустич. ветвь спиновых волн
ферримагнетиков, в
частности железоиттриевого граната (ЖИГ), у к-рого 20 подрешёток
и соответственно 20 ветвей спиновых волн (рис. 6). В табл. 1 приведены константы
акустич. ветви спиновых волн ЖИГ:
вектором k спиновой волны. Коэф. wобм
характеризует роль обменного взаимодействия магн. атомов, коэф. wм - магнитодипольного
взаимодействия. Ф-ла (12) описывает также акустич. ветвь спиновых волн
ферримагнетиков, в
частности железоиттриевого граната (ЖИГ), у к-рого 20 подрешёток
и соответственно 20 ветвей спиновых волн (рис. 6). В табл. 1 приведены константы
акустич. ветви спиновых волн ЖИГ:
Табл. 1.

Табл. 2.

В ЖИГ наиб. исследованы процессы релаксации спиновых волн. В чистых монокристаллах
теоретич. значения времён жизни релятивистских магнонов согласуются с экспериментом.
При комнатной температуре (300 К)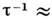 2,6*106 с-1 при
2,6*106 с-1 при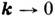
2) Двухподрешёточные одноосные антиферромагнетики с магнитной
анизотропией типа «лёгкая плоскость» имеют 2 акустич. ветви
спиновых волн (Н параллельно лёгкой плоскости):
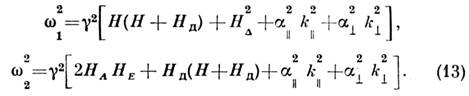
Здесь НА, НЕ - поля анизотропии и обмена,
НД - т. н. поле Дзялошинского, описывающее силу, приводящую
к слабому ферромагнетизму,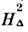 - слагаемое, определяемое слабыми взаимодействиями (сверхтонким, магнитоупругим),
- слагаемое, определяемое слабыми взаимодействиями (сверхтонким, магнитоупругим),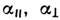 - константы неоднородного обмена (
- константы неоднородного обмена (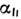 - вдоль оси симметрии кристалла,
- вдоль оси симметрии кристалла,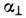 -
перпендикулярно к оси; табл. 2).
-
перпендикулярно к оси; табл. 2).
3) Двухподрешёточные антиферромагнетики с магн. анизотропией типа «лёгкая
ось» имеют 2 акустич. ветви спиновых волн, вырожденных при Н = 0:

(Н параллельно «лёгкой оси»). Величина щели при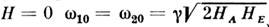 для большинства исследованных легкоосных антиферромагнетиков лежит в диапазоне
100 - 1000 ГГц.
для большинства исследованных легкоосных антиферромагнетиков лежит в диапазоне
100 - 1000 ГГц.
Спиновые волны в низкоразмерных системах, в кристаллах с большой энергией магнитной
анизотропии, в поликристаллах. В двумерных и одномерных системах, описываемых
моделью Гейзенберга, Спиновые волн нельзя трактовать как малое колебание, т. к.
даже при Т = Тс магн. упорядочение не наступает (в согласии
с Мёрмина - Вагнера теоремой). В подобных магнетиках при Т -
Тс возникают бесщелевые возбуждения - спиновые волн, у к-рых
скорость (если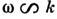 ) или эфф. масса (если
) или эфф. масса (если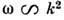 )
служит осн. характеристикой, отличающей низкотемпературную фазу (Т <
Тс)от высокотемпературной (Т > Тс).
)
служит осн. характеристикой, отличающей низкотемпературную фазу (Т <
Тс)от высокотемпературной (Т > Тс).
В нек-рых кристаллах (напр., CsCoCl3, FeF2) энергия магн. анизотропии не мала по сравнению с обменной энергией. При этом структура осн. состояния и спектр спиновых волн зависят от конкретного соотношения между обменной энергией и энергией анизотропии. Характерная особенность - сложная зависимость магн. характеристик от магн. поля, перестройка осн. состояния под действием магн. поля.
Длинноволновые спиновые волны 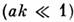 сохраняют смысл в поликристаллах .Дополнительное (по сравнению с
монокристаллами) затухание спиновых волн связано с рассеянием на границах кристаллитов.
сохраняют смысл в поликристаллах .Дополнительное (по сравнению с
монокристаллами) затухание спиновых волн связано с рассеянием на границах кристаллитов.
Спиновые волны в парамагнитных металлах и газах. В парамагнитных металлах спиновые волны предсказаны В. П. Силиным в 1960, обнаружены экспериментально в 1967. В немагн. металлах спиновые волны - колебания спиновой плотности электронов проводимости, обусловленные обменным взаимодействием между ними. Спиновые волны в немагн. металлах проявляются, напр., в селективной прозрачности металлич. пластин для эл--магн. волн с частотами, близкими частоте электронного парамагн. резонанса.
В классическом (невырожденном) газе частиц, обладающих спинами, наряду с упругими волнами за счёт обменного взаимодействия между атомами могут распространяться своеобразные волны, также называемые спиновыми. Они предсказаны в 1981, обнаружены в атомарном водороде из Не в 1984.

см. также лит. к ст. Ферромагнетизм, Антиферромагнетизм.
Л. А. Прозорова
(Фотометрический парадокс, парадокс Ольберса - это один из парадоксов космологии, заключающийся в том, что во Вселенной, равномерно заполненной звёздами, яркость неба (в том числе ночного) должна быть примерно равна яркости солнечного диска. Это должно иметь место потому, что по любому направлению неба луч зрения рано или поздно упрется в поверхность звезды.
Иными словами парадос Ольберса заключается в том, что если Вселенная бесконечна, то черного неба мы не увидим, так как излучение дальних звезд будет суммироваться с излучением ближних, и небо должно иметь среднюю температуру фотосфер звезд. При поглощении света межзвездным веществом, оно будет разогреваться до температуры звездных фотосфер и излучать также ярко, как звезды. Однако в дело вступает явление "усталости света", открытое Эдвином Хабблом, который показал, что чем дальше от нас расположена галактика, тем больше становится красным свет ее излучения, то есть фотоны как бы "устают", отдают свою энергию межзвездной среде. На очень больших расстояниях галактики видны только в радиодиапазоне, так как их свет вовсе потерял энергию идя через бескрайние просторы Вселенной. Подробнее читайте в FAQ по эфирной физике.
![]()