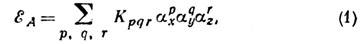
Магнитная анизотропия - зависимость магн. свойств (в узком смысле - намагниченности)от
выделенного направления в образце (магнетике). Существуют разл. виды М. а. Зависимость
намагниченности от её направления относительно кристаллографич. осей в кристаллах
наз. естественной кристаллографической М. а. Кроме того, М. а. может возникать
вследствие магнитоупругих деформаций, при наличии внеш. или внутр. напряжений
(наведённая М. а.), а также из-за анизотропии формы образца. М. а. существенно
влияет на процессы намагничивания п перемагничивания, на магнитную
доменную структуру п др. свойства магнетиков.
Энергию кристаллографич.
М. а. однородно намагниченного ферромагнетика можно записать в виде
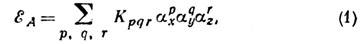
где 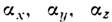 - направляющие косинусы вектора спонтанной намагниченности M, а р,
q, r - целые числа. Коэф. Кpar (р+q+r=2n)
наз. константой М. а. порядка п. В теории М. а. часто используется вместо
(1) разложение по сферич. гармоникам. Конкретный вид выражения (1) и число линейно
независимых коэф. Kpqr при данном п полностью определяются
симметрией кристалла. Константы М. а. являются функциями внеш. параметров:
температуры Т, давления Р и т. д.
- направляющие косинусы вектора спонтанной намагниченности M, а р,
q, r - целые числа. Коэф. Кpar (р+q+r=2n)
наз. константой М. а. порядка п. В теории М. а. часто используется вместо
(1) разложение по сферич. гармоникам. Конкретный вид выражения (1) и число линейно
независимых коэф. Kpqr при данном п полностью определяются
симметрией кристалла. Константы М. а. являются функциями внеш. параметров:
температуры Т, давления Р и т. д.
Из (1) следует, что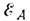 имеет
минимумы и максимумы при определённых значениях
имеет
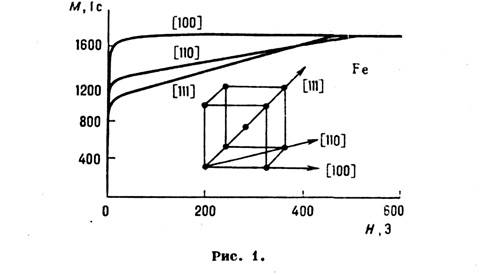
минимумы и максимумы при определённых значениях 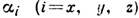 . Соответствующие направления наз. осями лёгкого намагничивания (ОЛН)
и трудного намагничивания. В отсутствие внеш. магн. поля Н вектор спонтанной
намагниченности М (внутри домена)направлен по ОЛН. В поле Н он поворачивается, приближаясь к направлению поля с возрастанием его величины.
Критич. значения Н=НA, при к-рых М устанавливается
по H при намагничивании в трудных направлениях, наз. полями анизотропии.
Значения НА связаны с константами М. а. Так, для кристалла
кубич. сингонии при намагничивании вдоль оси [110], а также для кристаллов гексагональной
сингонии HA = 2K/M. Типичные кривые намагничивания
монокристалла Fe с объёмноцентрированной кубич. решёткой приведены на рис. 1.
. Соответствующие направления наз. осями лёгкого намагничивания (ОЛН)
и трудного намагничивания. В отсутствие внеш. магн. поля Н вектор спонтанной
намагниченности М (внутри домена)направлен по ОЛН. В поле Н он поворачивается, приближаясь к направлению поля с возрастанием его величины.
Критич. значения Н=НA, при к-рых М устанавливается
по H при намагничивании в трудных направлениях, наз. полями анизотропии.
Значения НА связаны с константами М. а. Так, для кристалла
кубич. сингонии при намагничивании вдоль оси [110], а также для кристаллов гексагональной
сингонии HA = 2K/M. Типичные кривые намагничивания
монокристалла Fe с объёмноцентрированной кубич. решёткой приведены на рис. 1.
Константы М. а. могут быть
определены из эксперим. данных: 1) по площади кривых намагничивания 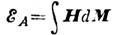 для разных кристаллографич. направлений; 2)
по измерению крутящих моментов в анизометре магнитном; 3) по закону приближения
магнетика к состоянию магн. насыщения (в поликристаллах); 4) по частоте ферромагнитного
резонанса. В нек-рых случаях (редкоземельные металлы) можно использовать
связь констант М. а. с анизотропией парамагн. восприимчивости. Значения Кп определены для большинства магн. материалов в широком интервале температур.
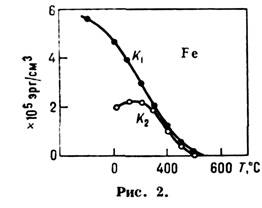
На рис. 2 приведены К1(Т)и К2(Т)для Fe
[в отличие от определения (1) нумерация констант М. а. здесь дана в
порядке их следования, без учёта констант, обращающихся в нуль из условий симметрии].
М. а. в ферри-магнетиках, антиферромагнетиках и слабых ферромагнетиках (см.
Ферримагнетизм, Слабый ферромагнетизм)имеет обычно более сложный характер,
чем в ферромагнетиках.
для разных кристаллографич. направлений; 2)
по измерению крутящих моментов в анизометре магнитном; 3) по закону приближения
магнетика к состоянию магн. насыщения (в поликристаллах); 4) по частоте ферромагнитного
резонанса. В нек-рых случаях (редкоземельные металлы) можно использовать
связь констант М. а. с анизотропией парамагн. восприимчивости. Значения Кп определены для большинства магн. материалов в широком интервале температур.
На рис. 2 приведены К1(Т)и К2(Т)для Fe
[в отличие от определения (1) нумерация констант М. а. здесь дана в
порядке их следования, без учёта констант, обращающихся в нуль из условий симметрии].
М. а. в ферри-магнетиках, антиферромагнетиках и слабых ферромагнетиках (см.
Ферримагнетизм, Слабый ферромагнетизм)имеет обычно более сложный характер,
чем в ферромагнетиках.
Теоретич. исследования
М. а. направлены на установление осн. микроскопии, механизмов возникновения
анизотропии и определение значений и температурной зависимости коэф. Кп. С точки зрения природы М. а. все магнетики делятся на два типа: спиновые
и орбитальные. К первым относятся магнетики на основе d-переходных элементов
(группы Fe), ко вторым - редкоземельные 4f-магнетики. Среди магнетиков
группы урана имеются представители обоих типов. В спиновых d-магнетиках
орбитальные моменты L электронов почти заморожены (см. "Замораживание"
орбитальных моментов), так что квантовомеханич. ср. значения 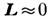 и магн. момент атомов (ионов) определяется величиной их спина. Спины S
сами по себе "не чувствуют" анизотропии кристалла. М. а. возникает
за счёт частичного размораживания моментов L cnuн-oрбumалъным взаимодействием (СОВ) с энергией
и магн. момент атомов (ионов) определяется величиной их спина. Спины S
сами по себе "не чувствуют" анизотропии кристалла. М. а. возникает
за счёт частичного размораживания моментов L cnuн-oрбumалъным взаимодействием (СОВ) с энергией 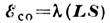 (
(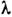 - постоянная
СОВ). При этом малый размороженный момент l ориентируется вдоль ОЛН,
ориентируя, в свою очередь, суммарный спиновый момент за счёт СОВ. Энергия М.
а. для этого случая (одноосная анизотропия)
- постоянная
СОВ). При этом малый размороженный момент l ориентируется вдоль ОЛН,
ориентируя, в свою очередь, суммарный спиновый момент за счёт СОВ. Энергия М.
а. для этого случая (одноосная анизотропия)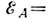
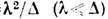 ,
где
,
где 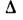 -
разность энергий электронов в состояниях, для к-рых матричный элемент L отличен
от нуля. Т. о., М. а. представляет собой результат совместного действия анизотропного
внутрикристаллического поля и спин-орбитального взаимодействия.
-
разность энергий электронов в состояниях, для к-рых матричный элемент L отличен
от нуля. Т. о., М. а. представляет собой результат совместного действия анизотропного
внутрикристаллического поля и спин-орбитального взаимодействия.
Ф. Блох и Г. Джентиль (F.
Bloch, G. Gentile, 1931), а затем Дж. Ван Флек (J. Van Vleck, 1937) рассмотрели
М. а. в модели локализованных спинов. Н. С. Акулов (1936) для кубич. кристаллов
и К. Зинер (С. Zener, 1954) в. более общем случае путём усреднения зависимости
энергии М. а. от отклонений магн. момента в поле кристалла получили температурную
зависимость Кп (при разложении по сферич. гармоникам):

где М - спонтанная
намагниченность. Ф-ла (2) была получена затем во мн. работах (в т. ч. в рамках
теории спиновых волн), однако её согласие с экспериментом в ряде случаев неудовлетворительно.
Так, напр., в металлах часто наблюдаются даже изменения знака Кп(Т). Имеются разл. попытки улучшения теории (в частности, путём учёта теплового
расширения магнетика), но осн. причина плохого согласия теории и эксперимента
связана, по-видимому, с неприменимостью модели локализованных спинов к зонным
маг-нетикам (см. Зонный магнетизм).
В d-металлах величина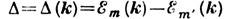 (т, т' - номера
вырожденных подзон, k - квазиимпульс электрона). Оценки
(т, т' - номера
вырожденных подзон, k - квазиимпульс электрона). Оценки 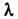 и
и 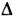 не очень
точны. При
не очень
точны. При 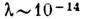 эрг,
эрг, 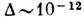 эрг значение
эрг значение
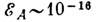 эрг. Т. о.,
эрг. Т. о.,
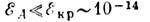 эрг, где
эрг, где 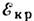 - энергия размороженного момента l во внутрикристаллич. поле. Намагничивание
в этом случае обусловлено отклонением S от ОЛН в меру отношения
- энергия размороженного момента l во внутрикристаллич. поле. Намагничивание
в этом случае обусловлено отклонением S от ОЛН в меру отношения 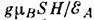 .
При этом l практически не отклоняется из-за большой величины
.
При этом l практически не отклоняется из-за большой величины 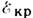 .
При
.
При 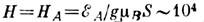 Э спиновая
намагниченность насыщается. Расчёты функции
Э спиновая
намагниченность насыщается. Расчёты функции для d-металлов (Е. И. Кондорский, 1971) показали сильную зависимость
М. а. от деталей зонной структуры магнетика.
для d-металлов (Е. И. Кондорский, 1971) показали сильную зависимость
М. а. от деталей зонной структуры магнетика.
В орбитальных 4/-магнетиках
М. а. определяется энергией полных атомных моментов J=L+S во внутрикристаллич.
поле. Энергия СОВ в этом случае велика.  (в противоположность d-магнетикам), в силу чего при намагничивании вектор
J вращается как единое целое, а константы М. а. определяются энергией
моментов J во внутрикристаллич. поле. Так, для одноосных кристаллов
(в противоположность d-магнетикам), в силу чего при намагничивании вектор
J вращается как единое целое, а константы М. а. определяются энергией
моментов J во внутрикристаллич. поле. Так, для одноосных кристаллов
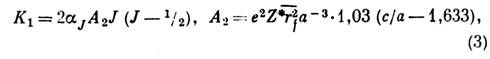
где 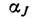 -
коэф. Стивенса, rf - радиус f-оболочки,
-
коэф. Стивенса, rf - радиус f-оболочки, 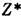 - эффективный заряд ина, с и а - параметры решётки. Ф-ла (3) соответствует
одноионной анизотропии и удовлетворительно согласуется с экспериментом как по
порядку величины (K1~108 эрг/см3), так
и по зависимости (через
- эффективный заряд ина, с и а - параметры решётки. Ф-ла (3) соответствует
одноионной анизотропии и удовлетворительно согласуется с экспериментом как по
порядку величины (K1~108 эрг/см3), так
и по зависимости (через 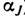 )
от номера элемента в ряду редкоземельных металлов (К1 меняет
знак между Но и Er, Nd и Рт, как это и наблюдается на опыте).
)
от номера элемента в ряду редкоземельных металлов (К1 меняет
знак между Но и Er, Nd и Рт, как это и наблюдается на опыте).
Помимо одноионного вклада
(3) в энергию М. а. существуют также т. н. двухионные вклады, обусловленные
анизотропным обменным взаимодействием магн. ионов и их диполь-дипольным взаимодействием.
Определение величины этих вкладов возможно по концентрац. зависимости Кп в сплавах. Существующие эксперим. данные указывают на преимущественно одноионный
характер М. а. в 4f-магнетиках.
Большая величина М. а.
в редкоземельных элементах имеет решающее значение для создания рекордно жёстких
магн. материалов (типа SmCo5), имеющих широкое техн. применение.
Высокие значения констант
М. а. наблюдаются также в нек-рых соединениях актинидов, напр. в US 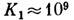 эрг/см3 (см. Актинидные магнетики).
эрг/см3 (см. Актинидные магнетики).

Ю. П. Ирхин
|
|