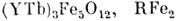(R - редкоземельный
элемент).Магнитоупругое взаимодействие - взаимное влияние намагниченности и упругих деформаций среды (связь спиновой подсистемы
кристалла с кристал-лич. решёткой). M. в. проявляется, напр., в изменении размеров
и формы тела (образца) при его намагничивании (магпитострикция), а также
в изменении намагниченности при деформации образца (магнитоупругпй эффект, или
Виллари, эффект).
Основные представления. M. в. обусловлено тем,
что осн. взаимодействия магн. моментов атомов или ионов в веществе, напр, обменное
взаимодействие, магн. диполь - дипольное взаимодействие, взаимодействие
магн. моментов с внутрикристаллическим полем, зависят от расстояния между
ними. Намагничивание кристалла изменяет характер этого взаимодействия, что проявляется
в изменении расстояний между частицами, а макроскопически - в деформации образца
(магнитострпкции). В свою очередь изменение расстояния между частицами, т. е.
деформация образца, изменяет силу взаимодействия между магн. частицами, а следовательно,
и их ср. магн. моменты, т. е. намагниченность образца, температуру Кюри, магн. анизотропию
и т. д.
Возникающая при намагничивании деформация приводит
к уменьшению отд. составляющих энергии образца - обменной энергии, энергии магн.
анизотропии, магнитодипольной энергии. Суммарное изменение энергии образца в
результате его деформации при намагничивании определяет магнитоупругую энергию
образца (пли энергию M. в.). С др. стороны, возникновение деформации вызывает
нек-рое увеличение энергии упругой деформации, но оно, конечно, меньше выигрыша
в энергии M. в., иначе не возникла бы магнитострикция.
Различают изотропный вклад в энергию M. в., обычно
имеющий обменное происхождение, и анизотропный, связанный с энергией магн. анизотропии.
Первый является причиной т. н. объёмной магнитоетрикции, к-рая вносит вклад
в тепловое расширение образца, обладает характерной аномалией в районе Кюри
точки, но не меняет кристаллогра-фич. симметрии вещества. Анизотропная часть
M. в. приводит к т. н. линейной магнитострикции и соответствующему изменению
кристаллографич. симметрии кристалла, в соответствии с изменением магнитной
симметрии.
M. в. оказывает влияние на фазовые переходы в
точках Кюри и Нееля (см. Магнитный фазовый переход ).Оно, в частности,
может быть ответственно за то, что эти фазовые переходы протекают как переходы
1-го рода. Давая в нек-рых материалах значит, вклад в энергию магн. анизотропии,
M. в. является причиной ориентационных фазовых переходов, например в
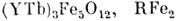(R - редкоземельный
элемент).
В динамике магнитоупорядоченных сред M. в. проявляется
как взаимодействие упругих волн, (фононов) и спиновых волн, приводящее
к возникновению магни-тоупругих волн. Для характеристики влияния M. в.
на динамич. процессы вводят коэф. магнитоупругой связи, к-рый представляет собой
отношение энергии M. в. в магнитоупругой волне к среднему геометрическому от
энергий упругой и спиновой подсистем. Для ферромагн. кристалла:
z = (cВ2/СМ2)1/2,
где С - модуль упругости материала, M - намагниченность, c - квазистатич. магнитная восприимчивость, В - характерное значение энергии M. в. (или, точнее, магнитоупругих параметров
M. в., см. ниже). Для типичных ферромагн. материалов: В ~ 106 -107 эрг/см3, С ~ 1012 эрг/см3,
M2 ~ 104 - 105 эрг/см3,
c ~ 1 и коэф. связи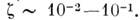
При такой слабой связи можно рассматривать волны, распространяющиеся в ферромагн.
кристалле, как невзаимодействующие чисто упругие и спиновые волны. Иная ситуация
возникает в условиях пересечения спектров упругих и спиновых волн, где M. в.
становится сильным и приводит к разнообразным интересным эффектам (например,
магнитоакустическому резонансу). Сильной магнитоупругой связью обладают
нек-рые соединения редкоземельных металлов и актинидов с металлами группы железа,
напр. TbFe2, UFe2, аморфные сплавы типа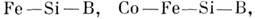 
а также
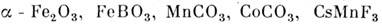и антиферромагн. кристаллы с анизотропией
типа "лёгкая плоскость"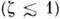 
.
В последних M. в. ответственно за существование энергии активации низкочастотных
спиновых волн - эффект магнитоупругой щели в спектре магнонов (А. С. Боровик-Романов,
E. Г. Рудашевский, E. А. Туров, В. Г. Шавров, 1964).
Под влиянием M. в. возникает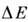 
-эффект
(см. Магнитострикция)и происходит изменение скорости звука иод воздействием
магн. поля, достигающее 50% и более в веществах с большим коэф. магнитоупругой
связи. Высокая чувствительность упругих модулей к воздействию магн. поля в таких
материалах является основой параметрич. магнитоупругих явлений (пара-метрич.
возбуждение магнитоупругих волн, преобразование спектра бегущих магнитоупругих
волн, генерация гармоник, управляемая фокусировка звука неоднородным магн. полем
и т. д.). M. в. ответственно за акустич. эффекты Фарадея и двойного лучепреломления,
а также эфф. энгармонизм упругой подсистемы (В. И. Ожогин, В. Л. Преображенский,
1977) [4].
M. в. широко используется в технике; в частности,
на нём основаны разнообразные магнитострикционные преобразователи.
M. в. представляет большой интерес для функциональной
электроники (управляемые магн. полем линии задержки, перестраиваемые резонаторы
и фильтры, фазовые модуляторы, конвольверы, анализаторы спектра и др.). В СВЧ-электронике
активно исследуют M. в. поверхностных акустич. волн с магнитостатическими
волнами в магн. плёнках (Y3Fe5O12, TbxFe1-31.
и др.).
Феноменологическое описание M. в. При теоретич.
описании M. в. широко используется феноменологич. подход, основанный на теории
симметрии кристаллов. Энергия M. в. записывается в виде разложения по инвариантным
полиномам, составленным из компонентов тензора упругих деформаций среды
eij
и компонентов многомерного параметра порядка, характеризующего магнитную
атомную структуру среды. В ферромагнетике (ФМ) в качестве параметра порядка
используют намагниченность M, в антиферромагнетико (АФМ) - векторы антиферромагнетизма
и намагниченности, в ферримагнетиках (ФИМ) - намагниченности магнитных подрешёток и т. д. Энергия M. в. является чётной функцией магн. параметров порядка, откуда
следует симметрия относительно инверсии времени (см. Магнитная симметрия).
Для ФМ в линейном приближении по eij
и квадратичном по компонентам намагниченности энергия M. в. может быть представлена
в виде
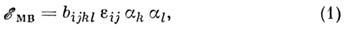
где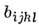 
-
тензор магнитоупругих постоянных, ai
- направляющие косинусы вектора намагниченности. В ф-ле (1) и далее суммирование
осуществляется по дважды встречающимся индексам.
Тензор четвёртого ранга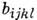
определяется
точечной симметрией кристалла; он имеет
в общем случае 36 независимых компонентов, однако условие 
оставляет
независимыми из них лишь 30. Конкретный
вид тензора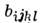
для разл. классов симметрии приведён, напр., в [1, 2]. Для кристаллов кубической
(классы симметрии TdO, Оh,) и гексагональной (классы
D3d, C3v, D6, D6h)синго-нии
энергия M. в. имеет вид
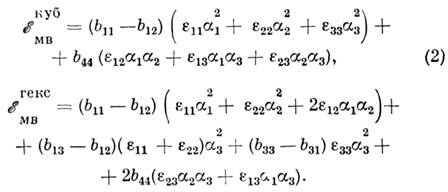
Здесь компоненты тензора bijkl записаны в матричных обозначениях Фогта.
Для кристаллов кубич. сингонии приняты обозначения:
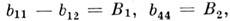с учётом к-рых
энергия M. в. принимает вид
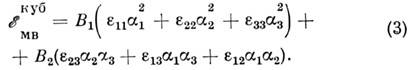
Магнитоупругие постоянные В1 и
В2 связаны с константами магнитострикции след, соотношениями
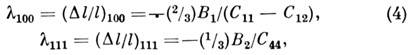
где С11, C12, C44
- упругие постоянные кубич. кристалла. В табл. приведены значения магнитоупругих
постоянных В1 и В2 для нек-рых магнитоупорядоченных
кристаллов.
Измерение магнитострикции является распространённым
методом определения констант M. в. Др. методы - ферромагн. резонанс (сдвиг частоты
резонанса под влиянием M. в.),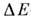
-эффект
и изменение скорости звука под влиянием магн. поля, динамич. магнитоакустич.
явления.
В ф-ле (1) магнитоупругие константы рассматриваются
как феноменологич. параметры, к-рые определяются экспериментально. В микроскопич.
теории M. в. эти параметры и их зависимость от температуры и магн. ноля определяются
для данного материала, исходя из его кристаллич. структуры и квантовомеханич.
характеристик магн. ионов. Выделяют M. в., основанное на магн. диполь-дипольном
взаимодействии, на анизотропном обмене и на комбинированном с участием спин-орбитального,
обменного взаимодействия и на внутрикристаллич. полях.
Для более полного описания M. в. в ф-лу (1) иногда
приходится вводить слагаемые более высокого порядка по направляющим косинусам
вектора намагниченности.
Ф-лу (1) можно использовать для описания M. в.
в магнитоупорядоченных кристаллах с неск. магн. под-решётками; нужно лишь произвести
в ней дополнит, суммирование по подрешёткам и учесть наличие перекрёстных
по подрешёткам слагаемых. Напр., для двухпод-решёточного коллинеарного АФМ
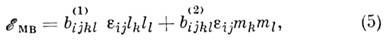
где l, т - единичные
векторы антиферромагнетизма и ферромагнетизма соответственно. В случае слабого
ферромагнетизма энергия M. в. содержит смешанные инварианты типа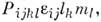 
ответственные за явления пьезомагнетизма и линейную магнитострикцшо. Энергию, соответствующую таким инвариантам,
наз. пьезомагнитной. В общем случае для определения вида энергии M. в. в многоподрешёточном
ФМ используют пространств, симметрию кристалла.
В феноменологич. теории M. в. предполагается,
что температурная зависимость магпитоупругих констант определяется тепловыми
флуктуациями магн. моментов. Усреднение по флуктуациям приводит к уменьшению
модуля намагниченности и вместе с ним к уменьшению коэффициентов в выражении
для энергии M. в. Температурная зависимость последних определяется законом:
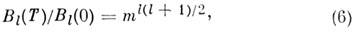
где l - степень полинома от сц в разложении
энергии M. в., Bl - коэф. полинома,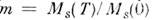 
- приведённая намагниченность. Напр., для
разложений (1-5), где l = 2, имеем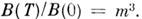 
Эксперим. и теоретич. исследования M. в. показали,
что энергия M. в. в форме (1) хорошо описывает магнитоупругие явления в тех
материалах, в к-рых магн. ионы, ответственные за формирование магн. порядка,
имеют в качестве осн. состояния орбитальный синг-лет, отделённый достаточно
большим энергетич. интервалом от возбуждённых уровней. Примером таких ионов
являются т. н. S-ионы, т. е. ионы, у к-рых в осн. состоянии орбитальный момент
L равен нулю (Fe3+, Mn2+, Gd3+, Eu2+
и др.), а также ионы с "замороженным" орбитальным моментом (Cr3+,
Ni2+ в октаэдрич. окружении и др.). Др. тип ионов - ионы, у к-рых
орбитальный момент в осн. состоянии отличен от нуля, напр, редкоземельные ионы,
Co2+ в ферритах и др. Для описания M. в. таких ионов используют микроскопич.
теорию.
Элементы атомно-микроскопической теории M. в.
Микроскопич. описание M. в. основывается на применении спинового гамильтониана. Оно позволяет установить связь магнитоупругих явлений с электронной структурой
магнетика, выяснить микроскопич. механизмы M. в., определить зависимость магнитоупругих
явлений от температуры, магн. поля, состава магнетика и др. факторов. В общем виде
спиновый гамильтониан M. в. представляет собой сумму элементарных взаимодействий
спиновых магн. моментов со смещениями ионов от положений равновесия, включающими
в себя упругие деформации (акустич. фононы) и смещения ионов внутри элементарной
ячейки (оптич. фононы). Различают спиновые гамильтонианы одноионного и двухионно-го
M. в.
Одноионное M. в. обусловлено смещениями ионов
кристалла при деформации, к-рые изменяют внутрикристаллич. поле, действующее
на магн. ион, и тем самым энергию ионов в отом поле. Двухионное M. в. обусловлено
зависимостью от деформации таких взаимодействий, как магнитодипольное, псевдодинольное,
обменное.
В случае материалов, содержащих ионы с нулевым
или "замороженным" орбитальным моментом, микроскопич. теория даёт
для энергии M. в. выражение того же вида, что и феноменологич. теория. В частности,
зависимость магнитоупругих констант от температуры T и магн. поля H полностью
определяется намагниченностью т (H, T) [Э. Каллен (E. Callen),
X. Каллен (H. Gallon). 1963]: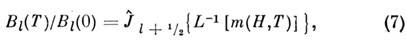
где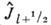 
-
приведённая функция Бесселя: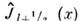 
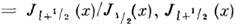- гиперболич. функция Бесселя, L~l(x)- обратная Ланжевена
функция [т(Н, T)=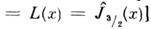 
. При достаточно низких температурах, когда можно пренебречь заселённостью всех
уровней, кроме основного и первого возбуждённого, ф-ла (7) приводит к известному
закону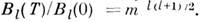
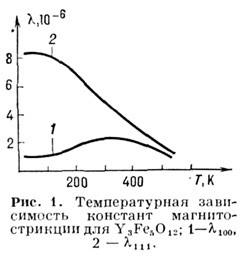
Проиллюстрировать сказанное можно на примере иттриевого
феррита-граната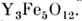 
В нём ионы Fe3+ являются ионами 5-типа. На рис. 1 приведены температурные
зависимости констант магнитострикцни в этом материале, построенные на основе
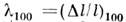ф-лы (7); на рис.2-полевая зависимость магнитострикции
и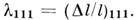 
Насыщение констант
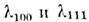происходит
в тех же полях, что и насыщение намагниченности.
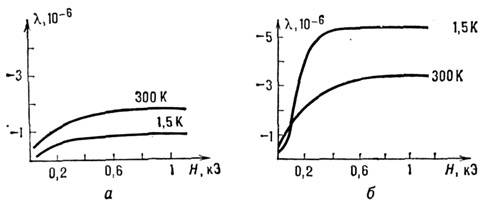
Рис. 2. Зависимость констант магнитострикции
Y3FebO12 от напряжённости магнитного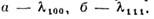
поля
при разных температурах;
Ионы с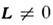
в
осн. состоянии обладают более разнообразными
полевыми и температурными зависимостями M. в. Оно также значительно больше по
величине, чем M. в. ионов с L = 0, поэтому в редкоземельных
соединениях, особенно при низких темп-pax, часто наблюдается т. н. гигантская
магнитострикция ~ 10-3-10-2 (К. П. Белов, Р. З.Левитин,
С. А. Никитин, В. И. Соколов, 1961 [3]).
Для определения температурной и полевой зависимости
энергии M. в. с помощью спинового гамильтониана нужно знать энергетич. спектр
и волновые функции иона. При низких темп-pax достаточно знать обычно один-два
ниж. уровня. Энергия M. в. ионов с синг-летным осн. состоянием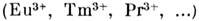 
имеет вид (в расчёте на один ион) [5]:
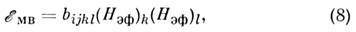
где Нэф - эфф. поле, действующее
на ион; магнитоупругие постоянные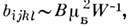 
W - характерная энергия, отделяющая
осн. уровень от возбуждённых (~10 -102 см''1), mВ - магнетон Бора, В ~ 102 - 103 см-1
- магнитоупругий коэффициент.
Энергия M. в. крамерсовских ионов, осн. состоянием
к-рых во внутрикристаллич. поле является дублет (Dy3+, Er3+,
Yb3+, ...), имеет вид
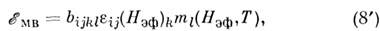
где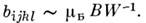
Температурная и полевая зависимости M. в. в этом
случае определяются произведениями типа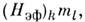
а не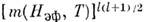
, как в
феноменологич. теории. Др. важная особенность
M. в. в материалах с такими ионами заключается в том, что их магнитоупругие
коэф. обладают сильной полевой зависимостью в области насыщения намагниченности
(в феноменологич. теории константы магнитострикции при этом от поля вообще не
зависят). Это обстоятельство обусловлено тем, что постоянные M. в. определяются
не только ниж. уровнями энергии, а гл. обр. возбуждёнными состояниями, что является
своеобразным аналогом ванфлековской восприимчивости в магнитоупругих явлениях
(см. Ванфлековский парамагнетизм).
Осн. состоянием некрамерсовских ионов в низкосимметричном
внутрикристаллич. поле часто является изолированный квазидублет, т. е. два близко
расположенных синглетных уровня, отделённых от возбуждённых уровней достаточно
большим энергетич. интервалом. Для приближённого описания M. в. этих ионов можно
использовать ф-лу (8). На рис. 3 приведена полевая зависимость магнитострикции
тербиевого и диспрозие-вого гранатов, хорошо иллюстрирующая особенности M. в.
в материалах с сильно анизотропными ионами, обладающими орбитальным моментом
в осн. состоянии.
Рис. 3. Зависимость магнитострикции тербий-галлиевого
граната (Tb3Ga5O12) от напряжённости магнитного
поля при 4,2 К: 1 - H || [111], 2 - H|| [110],
3 - Hперп || [111], 4 - H || [111], 5 - зависимость
намагниченности (в единицах mб/ион)
вдоль направления [111] от напряжённости
магнитного поля.
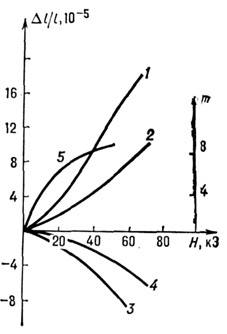
Для полей, где намагниченность стремится к насыщению
(H >~ 30 кЭ), характерно, что константы магнитострикции линейно увеличиваются
с ростом поля H, не проявляя к--л. тенденции к насыщению. Аналитич. зависимость
магнитострикции этого соединения от H и T может быть представлена ф-лой,
сильно отличающейся от тех, к-рые определяются феноменологич. теорией:
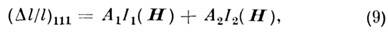
где
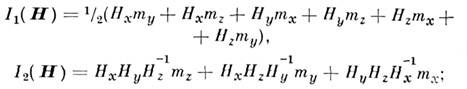
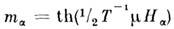- компоненты приведённой намагниченности редкоземельных ионов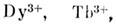
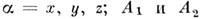- константы магнитострикции,
m - магн. момент иона.
Двухионное M. в. важно учитывать в низкосимметричных
материалах, а также в магнетиках кубической сингонии, обладающих сложной пространственной
и магнитной структурой, например в редкоземельных ферритах-гранатах.
Рис. 4. Зависимость констант магнитострикции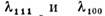
гольмий-иттриевого феррита-граната
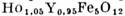от напряжённости магнитного поля при 78 К.
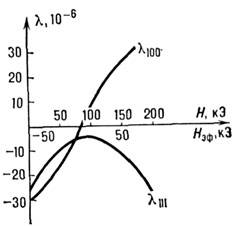
На рис. 4 приведена полевая зависимость констант
магнитострикции (HoY)3Fe5O12 при 78 К, хорошо
иллюстрирующая механизм двухионного M. в. Видно, что константы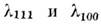
этого соединения существенно по-разному
зависят от поля: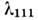
квадратично
меняется с полем, в то время как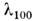
-
почти линейная функция Нэф. Это позволяет однозначно установить,
что l111 определяется одноионным механизмом, а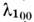
-
в основном двух ионным (обменным) M. в. Рис. 4 показывает также, что одноионный
и обменный механизмы M. в. дают сравнимые вклады в магннтострикцию редкоземельных
ферритов-гранатов.
Значительным M. в. обладают ионы Co2+
в ферритах, где преобладает одноионный механизм, что также обусловлено неполным
снятием орбитального вырождения осн. состояния [Дж. Слонзуски (J. Slonczewski),
19601.
Приведённые выше теории M. в. (как феноменологическая,
так и микроскопическая) не являются достаточно полными, т. к. рассматривают
взаимодействия маги, ионов с деформациями среды лишь в линейном по eik
приближении и не учитывают их взаимодействия с локальными вращениями среды.
Учёт квадратичных по eik
компонентов M. в. н взаимодействия магн. моментов с локальными поворотами
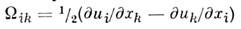
(здесь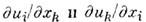
-
компоненты тензора механич. дисторсии) необходим
при анализе нек-рых эффектов, связанных с распространением звука в магнитоупоря-доченных
кристаллах, а также важен для теории симметрии: без учёта этих взаимодействий
энергия M. в. не удовлетворяет требованию вращат. инвариантности теории (симметрии
относительно группы непрерывных вращений) [7].
Локальные вращения среды возникают при распространении звука или при др. магнитоупругих процессах и создают локальную магн. анизотропию, действующую на магн. моменты. Отсюда следует, что энергия взаимодействия магн. моментов с локальными поворотами определяется параметрами магнитокристаллич. анизотропии и что это взаимодействие является особенно важным в материалах с большой величиной магн. анизотропии.
A. H. Звездин
|
|
 |
