Глоссарий по физике

Ферромагнетизм

Ферромагнетизм - магнитоупорядоченное состояние вещества, в к-ром большинство атомных магнитных моментов параллельны друг другу, так что вещество обладает самопроизвольной (спонтанной) намагниченностью. Ф. устанавливается при температуре Т ниже Кюри точки Т_C в отсутствие внеш. магн. поля Н. В более широком смысле Ф. наз. совокупность физ. свойств вещества в указанном состоянии. Вещества, в к-рых возникает ферро-магн. упорядочение магн. 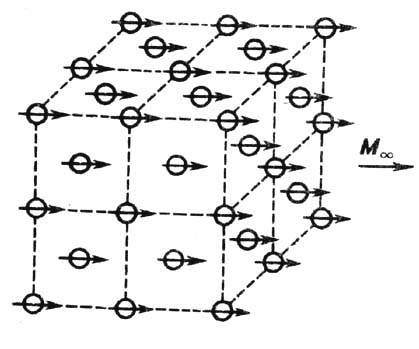моментов (рис. 1), наз. ферромагнетиками ,к их числу относятся как твёрдые кри-сталлич. вещества (см., напр., Магнитные диэлектрики, Магнитные полупроводники, Редкоземельные магнетики), так и нек-рые аморфные магнетики и металлические стёкла, а также магнитные жидкости .Ответственным за Ф. является обменное взаимодействие в м а г н е т и з м е, стремящееся установить спины (а следовательно, и магн. моменты) соседних атомов или ионов параллельно друг другу; в этом случае обменный интеграл имеет положит. значение.

Рис. 1. Ферромагнитная коллинеарная атомная структура в гранецентрированной кубической решётке ниже точки Кюри Т_C; стрелками обозначены направления атомных магнитных моментов.

Ф. обычно наблюдается в трёхмерных системах, однако возможно его возникновение и в реальных квазиодномерных и квазидвумерных системах (см., напр., Слоистые магнетики)без нарушения Мёрмина-Вагнера теоремы. Ферромагн. атомный порядок можно непосредственно наблюдать методом магнитной нейтронографии, к-рый позволяет также определить величины атомных магн. моментов в узлах кристаллич. решёток разл. типов и пространственное распределение плотности магн. момента вблизи них. Кроме нейтронов аналогичную информацию (в т. ч. о внутр. полях на ядрах) могут дать ядерный магнитный резонанс, а также мюонной спиновой релаксации метод и мёссбауэровская спектроскопия.

Магнитная восприимчивость ферромагнетиков может достигать значений 10⁴-10⁵ Гс/Э; их намагниченность М, возникающая во внеш. магн. поле H, растёт с его величиной нелинейно (см. Намагничивание)и в полях 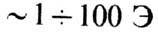может достигать магнитного насыщения, характеризуемого значением 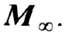Величина М зависит также от "магн. предыстории" образца, что приводит к неоднозначности функции M(H), или к гистерезису магнитному. При намагничивании и перемагничивании ферромагнетика происходит изменение. размеров и формы образца (см. Магнитострикция; )благодаря этому кривые намагничивания и петли гистерезиса зависят от внеш. напряжений. Наблюдаются также аномалии в величине и температурной зависимости упругих постоянных ферромагнетиков - т. н. DE-эффект и др. (см. Механострикция, Магнитомеха-нические явления), а также коэф. линейного и объёмного расширения. При адиабатич. намагничивании или размагничивании ферромагнетики изменяют свою температуру (см. Магнитокалорический эффект, Магнитное охлаждение). В ферромагн. монокристаллах наблюдается обычно резкая магнитная анизотропия (рис. 2). В поликрйсталлах с хаотич. распределением ориентации зёрен анизотропия в среднем по образцу отсутствует, но при однородном распределении этих ориентации она может возникать (см. Магнитная текстура). В результате конкуренции обменного и магн. дипольного взаимодействий происходит разбиение конечного ферромагн. образца на ферромагнитные домены (см. также Магнитная доменная структура ).Магн. и др. физ. свойства (в т. ч. электрич., тепловые, гальваномагн., магнитооптические) ферромагнетиков обладают ярко выраженной зависимостью от температуры, особенно вблизи Т_C. Спонтанная (при H=0) намагниченность M_s имеет максимум при 0 К и монотонно стремится к нулю при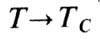(рис. 3). Выше Т_C ферромагнетик переходит в парамагн. состояние, а в нек-рых случаях (редкоземельные металлы)-в антиферромагнитное, что представляет собой частный случай магнитного фазового перехода 2-го рода. Магнитная проницаемость (или магн. восприимчивость) ферромагнетиков имеет резко выраженный максимум вблизи Т_C; при Т> Т_C уд. восприимчивость c обычно следует Кюри - Вепса закону. В более общих случаях в ферромагнетиках могут происходить ориентаци-онные фазовые переходы, при к-рых перестраивается магнитная атомная структура и изменяется магнитная симметрия ферромагнетика. Важный класс ферромагнетиков представляют собой магнитные сверхпроводники, в к-рых достигается сосуществование явлений Ф. и сверхпроводимости.

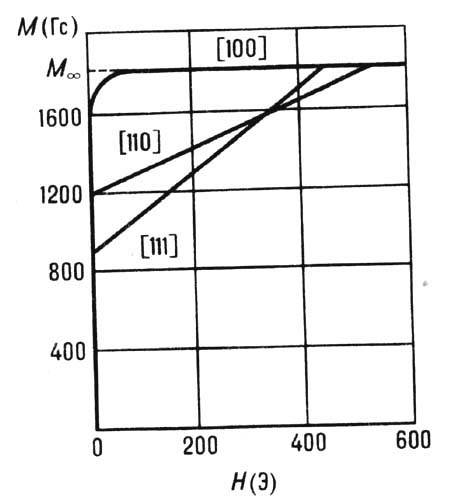
Рис. 2. Зависимость намагниченности М от магнитного поля для трёх главных кристаллографических осей монокристалла Fe (тип решётки - объёмнопентрированная кубическая, направление [100] -ось лёгкого, [110] - ось трудного и [111] - ось труднейшего намагничивания).

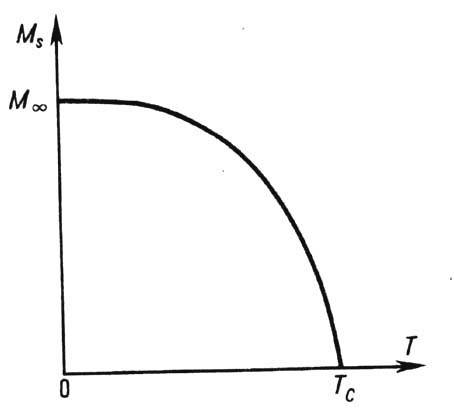
Рис. 3. Схематический ход температурной зависимости спонтанной намагниченности ферромагнетика; М_oo - значение M_s в состоянии магнитного насыщения, Т_C - точка Кюри.

Классификация и основные модели ферромагнетиков. Необходимый признак Ф. вещества - наличие постоянных (не зависящих от внеш. магн. полей) магн. (спиновых или орбитальных, либо тех и других вместе) моментов электронных оболочек у составляющих его атомов (ионов) (Fe, Со, Ni и др.). Однако при конденсации магнитно-активных атомов (ионов) в кристалл или аморфное тело их электронные оболочки часто претерпевают такую деформацию, что кристалл или аморфное тело уже не обладает в своих узлах пост. магн. моментами. Наиб. перестройке при конденсации подвергается самый наружный (валентный) слой электронной оболочки. Это обусловлено тем, что волновые функции валентных электронов у соседних атомов в твёрдом теле сильно перекрываются, что приводит к коллективизации бывших валентных электронов. В случае металлов они при этом образуют ферми-газ (или ферми-жидкость)электронов проводимости, а в неметал-лич. веществах - локализованные спин-насыщенные связи. В обоих случаях, как правило, для осн. состояния (T=0 К и H = 0) намагниченность М=0. Если атомы, из к-рых построен образец, не относятся к переходным элементам, то электронная оболочка ионных остовов в соответствии с Паули принципом имеет замкнутый характер и обладает диамагнетизмом .Более детальные исследования с помощью ядерного магнитного резонанса, Мёссбауэра эффекта и ядерной теплоёмкости обнаружили на атомных ядрах (Fe, Co, Ni и др.) очень сильные магн. поля - до 10⁵ - 10⁶ Э, источником к-рых являются "деформированные" внутренние 1s-, 2s- и 3s-слои оболочки ионных остовов. Электроны проводимости, подмагниченные благодаря обменному взаимодействию с d- или f-слоями атомной оболочки, участвуют в спонтанной намагниченности ферромагнетика.

В случае, когда ферромагнетик построен из атомов переходных элементов, в нём возможно сохранение не зависящего от внеш. поля магн. момента. При этом можно различать 4 осн. типа веществ: 1) металлич. вещества (чистые металлы, сплавы и соединения) на основе переходных элементов с недостроенными d-слоями (прежде всего 3d-слоями у атомов группы Fe); 2) металлич. вещества на основе переходных f-элементов [в первую очередь редкоземельных (РЗМ) с недостроенным 4f-слоем]; 3) неме-таллич. соединения при наличии хотя бы одного компонента из переходных d- или f-элементов; 4) сильно разбавленные растворы парамагн. ионов d- или f-элементов в диамагн. веществах. Появление во всех этих веществах атомного магн. порядка обусловлено обменным взаимодействием в магнетике. В неметаллич. веществах (тип 3) это взаимодействие носит косвенный характер (см. Косвенное обменное взаимодействие ),при к-ром магн. порядок электронных магн. моментов недостроенных d- или f-слоев в ближайших соседних парамагн. ионах устанавливается при активном участии электронов внешних замкнутых слоев магн--нейтральных ионов (О^2-, S^2-, Se^2- и т. п.), расположенных между магнитно-активными ионами. В большинстве случаев здесь устанавливается антиферромагн. порядок, к-рый может привести либо к чистому антиферромагнетизму ,если в каждой элементарной ячейке кристалла суммарный магн. момент всех ионов равен нулю, либо к ферримагнетизму или слабому ферромагнетизму, если он отличен от нуля. Есть такие случаи, когда взаимодействие и в неметаллич. веществах носит ферромагн. характер (все магн. моменты в ячейке параллельны). Общим для веществ типа 1, 2 и 4 является наличие в них системы ферми-частиц - коллективизированных (зонных) электронов проводимости. Эта система, хотя в ней существует подмагничивающая тенденция (обменные силы), как правило, не имеет магн. порядка и обладает парамагнетизмом Паули, если он не подавлен диамагнетизмом самих электронов проводимости или системы ионных остовов с замкнутыми оболочками. Парамагнетизм преобладает во всех непереходных металлах и большинстве переходных d-металлов (целиком группы Pd и Pt, а в группе Fe-у Sc, Тi и V).

Магн. порядок в металлич. веществах (тип 1, 2 и 4) различен по своему происхождению. Недостроенные 4f-слои ионов РЗМ-элементов (тип 2) имеют очень малый радиус по сравнению с параметром кристаллич. решётки, и поэтому волновые функции этих электронов у соседних узлов в кристалле или у соседей в аморфном теле практически не перекрываются. Следовательно, в таких веществах невозможен сколько-нибудь существенный прямой обмен. Его также нельзя ожидать и между сильно удалёнными друг от друга парамагн. d- или f-ионами в сильно разбавленных сплавах (тип 4). Т. о., следует ожидать, что в веществах типа 2 и 4 энергетич. параметр (обменный интеграл) прямого обмена исчезающе мал. Поэтому в таких веществах обменное взаимодействие, приводящее к магн. атомному порядку, должно носить характер косвенной связи магн. ионов через электроны проводимости, или т. н. РККИ-обменного взаимодействия. Наконец, в веществах типа 1 электроны; принимающие активное участие в атомном магн. порядке, состоят из бывших 3d-и 4s-электронов изолир. атомов. В отличие от 4f-слоев РЗМ-ионов, имеющих очень малый радиус, более близкие к периферии 3d-электроны атомов группы Fe испытывают более существенную коллективизацию и совместно с 4s-электронами образуют общую ферми-жидкость электронов проводимости. Однако в отличие от нормальных (непереходных) металлов, эта система в d-металлах обладает гораздо большей плотностью состояний вблизи поверхности Ферми, что благоприятствует обменным силам в их конкуренции с размагничивающими "тенденциями" фер-ми-газа (см. Паули парамагнетизм)и приводит к Ф. в Fe, Со, Ni и их многочисл. сплавах и соединениях. В последнее время начали интенсивно исследоваться т. н. к о н д о в-с к и е ф е р р о м а г н е т и к и (CeRh₃Be₂, CeSi_x и др.), в к-рых f-электроны (обычно от Се) частично делокализуют-ся за счёт Кондо эффекта .Эти вещества по ряду свойств напоминают РЗМ-ферромагнетики, а по другим - зонные магнетики на основе d-металлов; не совсем обычными свойствами обладают и а к т и н и д н ы е м а г н е т и к и, среди к-рых встречаются ферромагнетики.

В целом квантовая теория Ф. даёт возможность качественно понять возникновение Ф. как результата положит. обменного взаимодействия. Однако количественно она далека от завершения. В последовательной микроскопич. теории прежде всего нужно определить знак осн. энергетич. параметра обменного взаимодействия (e_об, см. в ст. Магнетизм). Для этого необходимо знать энергетич. спектр и волновые функции системы электронов, участвующих в Ф. Однако пока точных сведений об этих величинах нет, и поэтому приходится пользоваться приближёнными подходами. Существуют 3 осн. модели Ф.: а) модель локализованных атомных магн. моментов (см. Гейзенберга модель, а также полярная модель и Хаббарда модель; )б) модель коллективизированных электронов, предложенная Я. И. Френкелем и Э. Стонером (Е. Stoner) (см. Стокера модель, Зонный магнетизм); в) s - d(f )-обменная модель (см. Шубина-Вонсовского модель и Зинера модель ).В модели а) предполагается, что атомные магн. моменты жёстко локализованы около узлов решётки и не принимают участия в процессах переноса в веществе. Эта модель лучше всего подходит для описания магн. порядка в неме-таллич. веществах (тип 3). В модели б) предполагается, что в ферми-системе электронов проводимости сильная обменная связь делает энергетически более выгодным Ф. Эта модель лучше всего подходит для объяснения Ф. d-металлов. Наконец s-d (f)-обменная модель в известном смысле объединяет первые две, допуская подмагничи-вание системы электронов проводимости. Модель в) лучше всего подходит для описания веществ типа 2 и 4. Большое эвристич. значение имеет изучение сильно разбавленных растворов (тип 4), а также Кондо-решёток, поскольку выяснение условий "сохранения", а иногда и резкого увеличения магн. моментов в сплаве (за счёт поляризации окружающей атом примеси электронов проводимости диамагн. матрицы) по сравнению с их значением в изолир. парамагн. ионах может прояснить детали возникновения Ф. в d-металлах, их сплавах и соединениях.

Теория самопроизвольной намагниченности. Конкретные расчёты по всем трём моделям Ф. могут проводиться как в квазиклассич. и феноменологич. приближениях, так и с помощью квантовомеханич. методов, в т. ч. метода функционала спиновой плотности. При квазиклассич. описании Ф. учитывают введением молекулярного поля. В простейшем расчёте для газа из N электронных спинов (на основе Изинга модели)их можно разбить соответственно двум возможным проекциям на r "правых" и N-r = l "левых". Тогда относит. намагниченность системы "впра-во" равна y = (r-l)/N. Энтропия "газа" при пренебрежении взаимодействием между спинами равна S(y) = k]n(N\/rll! (k -Больцмана постоянная ).Если энергия "газа" U не зависит от у, то свободная энергия равна

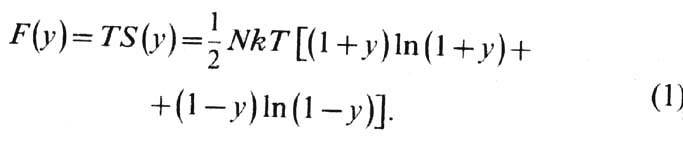
Из условия минимума (1) следует, что y = 0, т. е. Ф. отсутствует. Для его существования необходимо принять, что U зависит от у. В простейшем случае (гипотеза молекуляр-ного поля Вейса)

где А'>0-постоянная молекулярного поля, отнесённая к одному спину. Из условия минимума F(y)=-NA'y²-TS (у)находим:

где T_C = 2A'/k - точка Кюри. Ф-ла (3) даёт выражение для зависимости М_oo (Т)при H=0, качественно согласующееся с кривой на рис. 3.

В квазиклассич. и феноменологич. подходе были даны многочисл. уточнения приведённого расчёта. В частности, проводился учёт ближнего магн. порядка (метод Бете - Пайерлса - Вейса), развита термодинамич. теория ферромагн. превращения, в рамках к-рой был также рассмотрен вопрос о температурной зависимости разл. физ. свойств ферромагнетиков вблизи точки Кюри. Последние обычно описываются степенным законом типа (Т-Т_C)^a, где показатель степени a наз. критическим показателем. Эти показатели для намагниченности, теплоёмкости, восприимчивости вычисляются в рамках моделей Изинга, Гейзенберга и более общих схем, а также на основе ренормализационной группы по Вильсону (см. Эпсилон-разложение ).Более строгое уточнение приведённого выше расчёта дала квантовая механика, оправдавшая выбор зависимости (2) и объяснившая физ. природу параметра А' как меры обменной связи, зависящей от взаимной ориентации электронных спинов. Согласно Дираку (см. Обменное взаимодействие и Гейзенберга модель ),оператор обменной энергии системы электронных спинов имеет вид

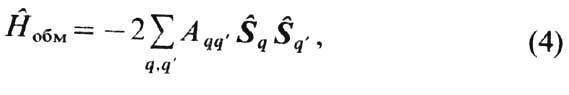
где 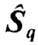-оператор вектора спина атома в узле q; A_qq'-- интеграл обмена между электронами в узлах q и q'. Если A_qq' резко падает с расстояниями между узлами, то можно ограничиться приближением ближайших соседей и, введя обозначение А_q,qb1=А, написать (4) в форме

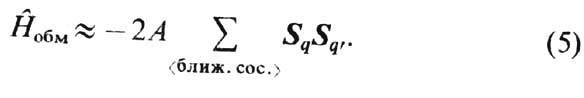
Квадрат суммарного спина всех N электронов равен

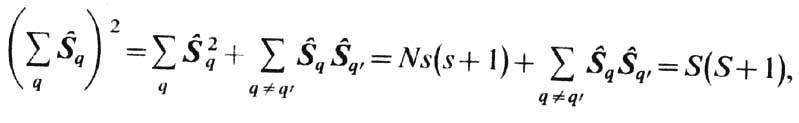
где S-полное спиновое квантовое число системы, a s - одного узла. Число членов парных произведений равно N(N-1). Поэтому ср. значение отд. члена этой суммы равно

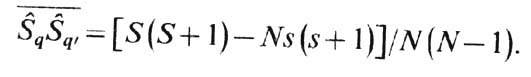
Число членов в сумме (5) равно (l/2)zN, где z-число ближайших соседей у узла решётки. Т. о., ср. значение гамильтониана системы равно

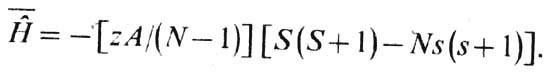
Поскольку s~ 1, a S-порядка намагниченности всей системы M=Ny (в единицах магнетона Бора m_B), то в ферромагнетике с точностью до членов ~1/N

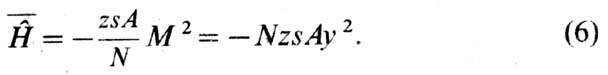
Этот расчёт проведён в т. н. п р и б л и ж е н и и э н е р г е т и ч е с к и х ц е н т р о в т я ж е с т и [4]. Из сравнения (6) и (2) видно, что параметр А' квазиклассич. теории определяется обменной энергией А, т. е. A' = zsA. Для определения величины и знака А нужна более точная теория, к-рую дают, напр., микроскопич. расчёты обменных взаимодействий в металлах методом функционала спиновой плотности, исходя лишь из кристаллич. структуры и порядкового номера в таблице Менделеева [11]. Используются также нек-рые усложнения гейзенберговского гамильтониана, напр. с помощью учёта неск. типов обменных интегралов между разл. соседями в узлах решётки (подробнее см. Спиновый гамильтониан ).При низких Т, используя метод вторичного квантования, удалось провести более точный расчёт энергетич. спектра ферромагнетика. Ограничиваясь состояниями, близкими к основному (при О К), в к-ром спины всех магнитно-активных электронов взаимно параллельны, можно найти собств. значения оператора (5), имеющие вид суммы энергий отд. элементарных возбуждений (квазичастиц) - спиновых волн, или ф е р р о-м а г н о н о в. Каждый ферромагнон несёт с собой магн. возбуждение системы и уменьшает 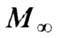на величину магн. момента одного узла решётки. С ростом Т возбуждается всё больше спиновых волн. Пока их мало, они образуют идеальный газ бозевских квазичастиц (см. Бозоны; )с ростом Т их число растёт ~T^3/2; поэтому температурная зависимость 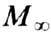вблизи 0 К имеет вид

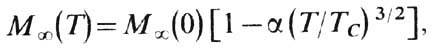
где 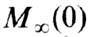-предельное значение 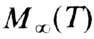при 0 К (см. Блоха закон ).Знание спектра спиновых волн важно для изучения явления ферромагнитного резонанса, распространения упругих колебаний в ферромагнетике и всего комплекса физ. свойств при низких температурах.

Применение квантово-статистич. методов (см. Грина функция, Матрица плотности)открывает новые возможности для построения более точной микроскопич. теории Ф. В частности, в рамках локализов. модели из этой теории следует, что при 0 К ср. атомный магн. момент, приходящийся на один узел, должен быть кратен m_B. Однако опыт показывает, что особенно в d-металлах, сплавах и соединениях эта величина заметно меньше момента изо-лир. атома (иона) и, кроме того, она существенно дробная (в единицах m_B). Это противоречие модели локализов. спинов с опытом связано с пренебрежением коллективизацией 3d-электронов в металле, а также обменным s - d (f)-взаимодействием.

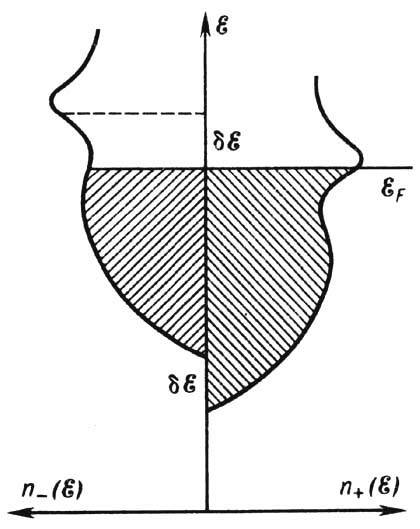
Рис. 4. Схематическое изображение смещения на 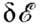кривых плотностей электронных состояний пb(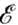)для "правых" ( + ) и "левых" ( -) спинов, обусловленного обменным взаимодействием, в энергетической полосе проводимости d-металла; 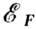- ферми-энергия.

В рамках зонной модели Ф. эта трудность в принципе исчезает (см. Зонный магнетизм ).Ф. в ферми-газе возможен при спонтанном "сдвиге" на энергии уровней в подполосе для "правых" и "левых" спинов, обусловленном обменным взаимодействием (рис. 4). При таком сдвиге, для того чтобы в равновесии ферми-энергия 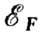в подполосах была одинаковой, надо v электронов на атом перенести из левой подполосы в правую. Это увеличивает кинетич. энергию на атом на величину 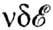(если число v не очень велико). Обменная энергия определяется связью пар электронов; она пропорц. квадрату числа электронов в каждой подполосе (числа электронов в единице объёма в правой и левой подполосах равны п₊ и п_). В парамагн. состоянии п₊=п_=п/2. Изменение энергии системы при переходе из пара- в ферромагн. состояние равно

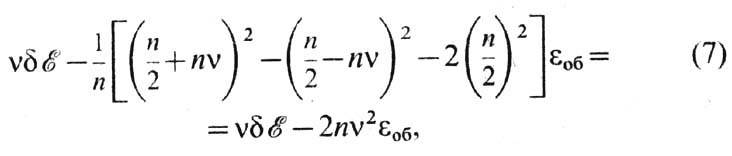
где e_об-ср. обменная энергия на пару электронов. Отношение 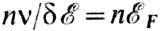определяет плотность электронных уровней (рис. 4) около ферми-энергии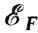. Если ввести безразмерный параметр , то из (7) следует, что при h> 1 в равновесии имеет место Ф., а при h<1-парамагнетизм. Условие, или критерий, для Ф. (h>1) легче выполняется в металлах с большими плотностями состояния при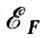 и большей энергией e_об. Из рис. 4 видно, что ср. атомный момент отнюдь не должен быть целочисленным в единицах m_B и равняться его значению для изолир. атома (иона).

Недостатком зонной модели является неучёт корреляц. энергии, к-рая может существенно изменить все количеств. и даже качеств. оценки приведённого расчёта (напр., критерий Ф.). Получены и более точные результаты, напр. при использовании метода расчёта с функционалом спиновой плотности. Помимо этого, зонная модель Ф. получила существ. развитие в работах, начатых Мория [22], в к-рых был произведён учёт спиновых флуктуации в ферромагн. системе электронов проводимости металлов и сплавов.

s - d(f)-обменная модель позволяет учесть не только пассивную роль электронов проводимости (напр., их под-магничивание со стороны "магнитных" f-слоев в РЗМ-ме-таллах), но и их активное участие в самом процессе установления Ф. благодаря косвенному РККИ-взаимодейст-вию. Качественно это можно описать так. Если ср. относит. намагниченность d(f)-электронов на узел равна m_d(f), а электронов проводимости-m_s, то энергия s - d(f)-обмена на узел равна , где A_sd(f) - параметр s -d(f)-связи. Добавка к ферми-энергии, связанная с намагниченностью электронов проводимости, равна (1/2)А_Фт_s², где 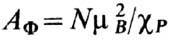и 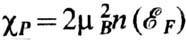- спиновая парамагн. восприимчивость (см. Паули парамагнетизм ).При квадратичном законе дисперсии электронов 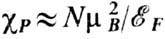, так что 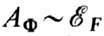. Полная энергия на узел, зависящая от m_d(f) и m_s, равна

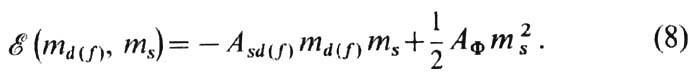
Энтропия сильно вырожденного газа электронов проводимости в металлах очень мала; поэтому равновесные значения m_d(f) и m_s находят из условия минимума энергии (8) при условиях: 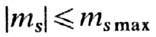и . Одно из возможных решений имеет вид

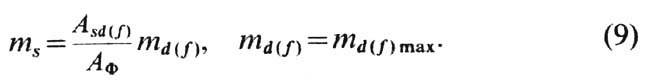
Отношение 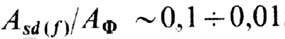; m_s составляе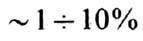т от 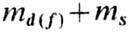. Подстановка (9) в (8) даёт

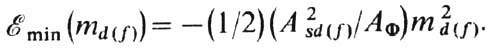
Т. о., эфф. параметр косвенного обмена типа РККИ между внутренними d(f)-электронами, взаимодействующими с электронами проводимости, равен

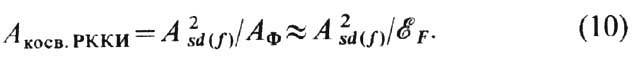
В данном приближении он всегда >0, т. е. способствует Ф. Более точный расчёт (10) показывает, что обмен типа РККИ сравнительно дальнодействующий (~ 1/r³) и носит осциллирующий знакопеременный характер.

Обменная s - d(f)-модель позволяет также установить связь между электронами проводимости РЗМ-металлов и особенностями их атомной магн. структуры, к-рая имеет вид неколлинеарных винтовых структур. Эта модель, если её дополнить учётом магн. (спин-орбитального) взаимодействия, позволяет также объяснить в принципе все аномалии электронных свойств ферромагнетиков, связанных с существованием в них спонтанной намагниченности. Учёт магн. (релятивистских) взаимодействий позволяет объяснить природу магн. анизотропии и магнитострикции.

Ещё в 1947 Ж, М. Латтинжер и Л. Тисса [12] высказали гипотезу о возможности существования "дипольного ферромагнетизма" в системе свободно вращающихся магн. диполей даже в отсутствие обменного взаимодействия или при весьма слабом обменном взаимодействии. Экспериментально такой Ф. обнаружен в 1990 [13] в образце ГЦК-структуры РЗМ-соли Cs₂NaR(NO₂)₆ (где R = Dy, Er, Gd, Nd), в к-рой магн. ионы находятся на достаточно удалённом расстоянии и поэтому обменная связь (~10 мК) на порядок меньше дипольной энергии (~100 мК), а точки Кюри расположены в интервале К.

Теория кривой намагничивания ферромагнетиков.

Из опыта известно, что при H=0 термодинамическому устойчивому состоянию макрообразца (минимуму термодинамич. потенциала) отвечает размагниченное состояние, ибо в противном случае на поверхности образца, как правило, образуются магн. полюса, создающие размагничивающее поле, с к-рым связана большая положит. энергия. Т. о., возникает тенденция размагничивания конечных образцов, хотя обменные силы стремятся их "намагнитить".

В результате происходит разбиение фсрромагн. образца на макрообласти однородной намагниченности. Эту гипотезу высказал ещё в 1907 П. Вейсс (P. Weiss). Теория Ф. качественно определяет размеры и форму доменов, к-рые зависят от конкуренции разл. взаимодействий внутри ферромагнетика. Равновесная структура доменов при Н=0 имеет вид совокупности связанных замкнутых магн. потоков внутри образца. Наряду с осн. доменами могут возникать и вторичные, т. н. з а м ы к а ю щ и е, домены. Магн. доменная структура является весьма структурно чувствительной. Между доменами образуются промежуточные слои, или стенки (см. Доменная стенка, Блоха стенка, Нееля стенка), конечной толщины, в к-рых вектор непрерывно меняет своё направление от ориентации, отвечающей вектору 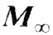в одном домене, до ориентации, отвечающей направлению 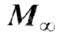его соседа. На образование этих стенок затрачивается положит. энергия, но её величина по всему образцу меньше энергии поля 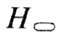, к-рая возникла бы в отсутствие доменов. При нек-рых критически малых размерах ферромагн. образцов возникновение в них неск. доменов может стать энергетически невыгодным, тогда частицы остаются при Т<Т_C однородно намагниченными (см. Однодоменные частицы ).Этим объясняются особые свойства тонких ферромагн. порошков и изделий из них (см. Магнитно-твёрдые материалы ).Среди них получили довольно широкое распространение коллоидные растворы однодоменных ферромагн. частиц, образующих магн. жидкости, имеющие перспективные области применения в технике и медицине. Весьма специфич. характер носит ферромагн. доменная структура в гонкой магнитной плёнке (см. также Цилиндрические магнитные домены). Кривые намагничивания и петли гистерезиса в ферромагнетиках, т. е. все процессы перемагничивания, определяются, в первую очередь, изменениями доменной структуры во внеш. магн. поле H, т. е. путём изменения объёма доменов с разл. 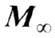ориентацией векторов в них за счёт смещения границ доменов (см. Доменной стенки динамика, Доменопродвигаюшая структура). Кроме того, играет роль и вращение векторов 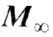в направлении внеш. поля. В размагниченном состоянии (с точностью до объёма, занятого доменными стенками) имеем

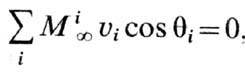
, где суммирование идёт по всем i-м доменам; u_i - объём i-го домена; q_i-угол между вектором 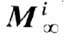в i-м домене и любой фиксир. осью в образце, напр. совпадающей с ориентацией намагничивающего поля. При включении поля вдоль этой оси в направлении поля появляется отличная от нуля намагниченность:

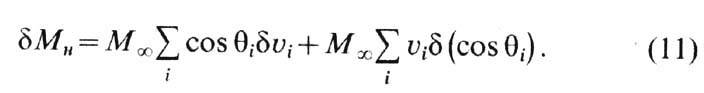
Первое слагаемое в (11) обусловлено ростом объёмов доменов, 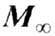в к-рых направлены относительно Н энергетически более выгодно, за счёт объёмов доменов, намагниченных менее выгодно; всё это осуществляется путём процессов смещения доменных стенок. Второе слагаемое в (11) обусловлено процессами вращения векторов 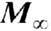. Уд. магн. восприимчивость ферромагнетиков, т. о., приближённо равна сумме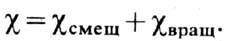 Анализ реальных кривых показывает, что в слабых полях а в более сильных (после крутого подъёма кривой)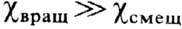 При размагничивании ферромагнетика из состояния магн. насыщения происходит восстановление доменной структуры путём возникновения з а р о д ы ш е й п е р е м а г н и ч и-в а н и я - областей с обратной (по отношению к первоначальной) намагниченностью. В. Дёрингом (W. Doring) в 1939 была разработана достаточно строгая и общая теория роста таких зародышей, к-рая хорошо подтверждена экспериментально [9, 4].

Из-за структурной чувствительности доменной структуры и процессов намагничивания и перемагничивания количеств. теория кривых намагничивания и петель гистерезиса ферромагнетиков находится в нач. стадии развития. Лишь в случае расчёта кривых намагничивания идеальных монокристаллов определ. формы в области, где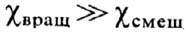 [1 ], можно развить строгую количеств. теорию для образцов простой формы (напр., эллипсоидов), допускающей однородность намагниченности при их структурной и хим. однородности. Теория кривых намагничивания и петель гистерезиса имеет важное значение для разработки новых и улучшения существующих магнитных материалов, играющих весьма важную и всё возрастающую роль в совр. технике (напр., в магн. дефектоскопии и структурном анализе, а также при конструировании элементов памяти ЭВМ, ускорительных секций, накопительных колец и т. п.).

Литература по

1. Акулов Н. С, Ферромагнетизм, М.- Л., 1939; 2) Бо-зорт Р., Ферромагнетизм, пер. с англ., М., 1956; 3) Вонсов-ский С. В., Шур Я. С., Ферромагнетизм, М.- Л., 1948; 4) Вон-совский С. В., Магнетизм, М., 1971; 5) Д орфман Я. Г., Магнитные свойства и строение вещества, М., 1955; 6) Туров Е. А., Физические свойства магнитоупорядоченных кристаллов, М,, 1963; 7) Вонсовский С. В., Изюмов Ю. А., Электронная теория переходных металлов, "УФН", 1962, т. 77, в. 3, с. 377; 1962, т. 78, в. 1, с. 3; 8) Теория ферромагнетизма металлов и сплавов. Сб. ст., пер. с англ., М., 1963: 9) Becker R., Doring W., Ferromagnetismus, В., 1939; 10) Kneller E., Ferromagnetismus, В.-[u.a.], 1962; 11) Magnetism, A treatise on modern theory and materials, ed. by G. T. Rado, H. Suhl, v. 1. Magnetic ions in insulators, their interactions, resonances and optical properties, N. Y.- L., 1963; v. 2A. Statistical models, magnetic symmetry, hyperfme interactions and metals, N. Y.-L., 1965; v. 2B. Interactions and metals, N. Y.-L., 1966; v. 3. Spin arrangements and crystal structure, domains and micromagnetics, N. Y.- L., 1963; v. 4; Herring С. (сост.), Exchange interactions among itinerant electrons, N. Y.- L., 1966; 12) Luttinger J. M., Tisza L., Theory of dipole interaction in crystals, "Phys. Rev.", 1946, v. 70, p. 954; 1947, v. 72, p. 257; 13) Roser M. R., Corruccini L. R., Dipolar ferromagnetic order in a cubic system, "Phys. Rev. Lett.", 1990, v. 65, p. 1064; 14) Тябликов С. В., Методы квантовой теории магнетизма, 2 изд., М., 1975; 15) Нагаев Э. Л., Физика магнитных полупроводников, М., 1979; 16) Уайт Р., Квантовая теория магнетизма, пер. с англ., 2 изд., М., 1985; 17) Тикадзуми С., Физика ферромагнетизма. Магнитные свойства вещества, пер. с япон., М., 1983; 18) Никитине. А., Магнитные свойства редкоземельных металлов и их сплавов, М., 1989; 19) Куркин М. И., Туров Е. А., ЯМР в магнитоупорядоченных веществах и его применения, М., 1990; 20) Тикадзуми С., Физика ферромагнетизма. Магнитные характеристики и практические применения, пер. с япон., М., 1987; 21) Изюмов Ю. А., Скрябин Ю. Н., Статистическая механика магнитоупорядоченных систем, М., 1987; 22) Мория Т., Спиновые флуктуации в магнетиках с коллективизированными электронами, пер. с англ., М., 1988; 23) Анисимов В. И. и др., Зонная теория магнетизма металлов и сплавов, "УФН", 1988, г. 155, в. 4, с. 721; 24) Ирхин В. Ю., Каднельсон М. И., Проблема кондовских магнетиков, "Физ. мет. и металловед.", 1991, № 1, с. 16; 25) Вон-совский С. В., Изюмов Ю. А., Курмаев Э. 3., Сверхпроводимость переходных металлов, их сплавов и соединений, М., 1977; 26) Вонсовский С. В., Кацнельсон М. И., Трефилов А. В., Локализованное и делокализованное поведение электронов в металлах, "Физ. мет, и металловед.", 1993, т. 76, в. 3, с. 3; в. 4, с. 3.
   

   С. В. Вонсовский.

   
   

   к библиотеке   к оглавлению   FAQ по эфирной физике   ТОЭЭ   ТЭЦ   ТПОИ   ТИ  
   
   
   Знаете ли Вы, что такое мысленный эксперимент, gedanken experiment?
   Это несуществующая практика, потусторонний опыт, воображение того, чего нет на самом деле. Мысленные эксперименты подобны снам наяву. Они рождают чудовищ. В отличие от физического эксперимента, который является опытной проверкой гипотез, "мысленный эксперимент" фокуснически подменяет экспериментальную проверку желаемыми, не проверенными на практике выводами, манипулируя логикообразными построениями, реально нарушающими саму логику путем использования недоказанных посылок в качестве доказанных, то есть путем подмены. Таким образом, основной задачей заявителей "мысленных экспериментов" является обман слушателя или читателя путем замены настоящего физического эксперимента его "куклой" - фиктивными рассуждениями под честное слово без самой физической проверки.
   Заполнение физики воображаемыми, "мысленными экспериментами" привело к возникновению абсурдной сюрреалистической, спутанно-запутанной картины мира. Настоящий исследователь должен отличать такие "фантики" от настоящих ценностей.

   Релятивисты и позитивисты утверждают, что "мысленный эксперимент" весьма полезный интрумент для проверки теорий (также возникающих в нашем уме) на непротиворечивость. В этом они обманывают людей, так как любая проверка может осуществляться только независимым от объекта проверки источником. Сам заявитель гипотезы не может быть проверкой своего же заявления, так как причина самого этого заявления есть отсутствие видимых для заявителя противоречий в заявлении.

   Это мы видим на примере СТО и ОТО, превратившихся в своеобразный вид религии, управляющей наукой и общественным мнением. Никакое количество фактов, противоречащих им, не может преодолеть формулу Эйнштейна: "Если факт не соответствует теории - измените факт" (В другом варианте " - Факт не соответствует теории? - Тем хуже для факта").

   Максимально, на что может претендовать "мысленный эксперимент" - это только на внутреннюю непротиворечивость гипотезы в рамках собственной, часто отнюдь не истинной логики заявителя. Соответсвие практике это не проверяет. Настоящая проверка может состояться только в действительном физическом эксперименте.

   Эксперимент на то и эксперимент, что он есть не изощрение мысли, а проверка мысли. Непротиворечивая внутри себя мысль не может сама себя проверить. Это доказано Куртом Гёделем.

   Понятие "мысленный эксперимент" придумано специально спекулянтами - релятивистами для шулерской подмены реальной проверки мысли на практике (эксперимента) своим "честным словом". Подробнее читайте в FAQ по эфирной физике.

   НОВОСТИ ФОРУМА Рыцари теории эфира

   10.11.2021 - 12:37: ПЕРСОНАЛИИ - Personalias -> WHO IS WHO - КТО ЕСТЬ КТО - Карим_Хайдаров. 10.11.2021 - 12:36: СОВЕСТЬ - Conscience -> РАСЧЕЛОВЕЧИВАНИЕ ЧЕЛОВЕКА. КОМУ ЭТО НАДО? - Карим_Хайдаров. 10.11.2021 - 12:36: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ - Upbringing, Inlightening, Education -> Просвещение от д.м.н. Александра Алексеевича Редько - Карим_Хайдаров. 10.11.2021 - 12:35: ЭКОЛОГИЯ - Ecology -> Биологическая безопасность населения - Карим_Хайдаров. 10.11.2021 - 12:34: ВОЙНА, ПОЛИТИКА И НАУКА - War, Politics and Science -> Проблема государственного терроризма - Карим_Хайдаров. 10.11.2021 - 12:34: ВОЙНА, ПОЛИТИКА И НАУКА - War, Politics and Science -> ПРАВОСУДИЯ.НЕТ - Карим_Хайдаров. 10.11.2021 - 12:34: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ - Upbringing, Inlightening, Education -> Просвещение от Вадима Глогера, США - Карим_Хайдаров. 10.11.2021 - 09:18: НОВЫЕ ТЕХНОЛОГИИ - New Technologies -> Волновая генетика Петра Гаряева, 5G-контроль и управление - Карим_Хайдаров. 10.11.2021 - 09:18: ЭКОЛОГИЯ - Ecology -> ЭКОЛОГИЯ ДЛЯ ВСЕХ - Карим_Хайдаров. 10.11.2021 - 09:16: ЭКОЛОГИЯ - Ecology -> ПРОБЛЕМЫ МЕДИЦИНЫ - Карим_Хайдаров. 10.11.2021 - 09:15: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ - Upbringing, Inlightening, Education -> Просвещение от Екатерины Коваленко - Карим_Хайдаров. 10.11.2021 - 09:13: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ - Upbringing, Inlightening, Education -> Просвещение от Вильгельма Варкентина - Карим_Хайдаров.