к библиотеке к оглавлению FAQ по эфирной физике ТОЭЭ ТЭЦ ТПОИ ТИ

РЕАЛЬНАЯ ФИЗИКА

Глоссарий по физике

А Б В Г Д Е Ж З И К Л М Н О П Р С Т У Ф Х Ц Ч Ш Э Ю Я

Критические показатели (критические индексы)

Критические показатели (критические индексы) - показатели степеней в степенных зависимостях термодинамич. величин от температуры, давления, плотности и т. д. вблизи точки фазового перехода 2-го рода (или критические точки). Типичная зависимость, например, теплоёмкости Су от температуры Т имеет вид:

где Т_с - темп-pa фазового перехода, 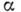- К. п. теплоёмкости. Кроме того, существует ряд К. п., характеризующих пространственное поведение корреляц. функций вблизи точки перехода. Осн. К. п. приведены в табл. 1.

Табл. 1.


Величины	Теплоёмкость	Восприимчивость	Средний параметр порядка	Радиус корреляции	Функция корреляции
Обозначения
h = 0
T=Т_c

Здесь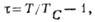 h -обобщённое внеш. поле,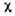-обобщённая восприимчивость.

Табл. 2. - Критические показатели одноконповентных систем


Показатель	Эксперимент		Теория
Показатель	Жидкости	Одноосные магнетики	Высокотемпературные ряды	-разложение	Суммирование -разложений

	0, 12b0,04	0,08-0, 1	0,11-0, 13	0,077	0, 11b b0,05
	0,34b0,01	0,33-0,35	0,312b0,05	0,340	0,325b b0,0015
	1, 22b0,02	1, 15b0,02	1,245-1,250	1,244	1,241b b0,O02
	4,6b0,2		5,0-5,2	4,46
	0,05b0.01		0,055b0,010	0,037	0,031b b0,004

Согласно общей теории фазовых переходов 2-го рода, К. п. определяется набором размерностей независимых флуктуирующих величин А_i, при масштабном преобразовании 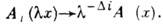Размерности 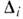обладают свойством универсальности, т. е. зависят только от размерности системы d-2,3 и симметрии параметра порядка (известные исключения из этого правила связаны для d=3 с наличием дальнодействующих сил, как, напр., в одноосных сегнетоэлектриках). Требование масштабной инвариантности приводит к установлению ряда соотношений между К. п., напр.

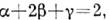
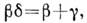
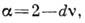
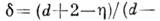
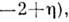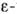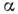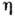так что независимыми являются лишь два К. п. Осн. методами приближённого вычисления К. п. являются метод ренормализационной группы (разложение) и исследование высокотемпературных разложений. Фактически в большинстве случаев К. п. и оказываются численно малыми 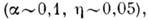что позволяет определить остальные ("большие") К. п.: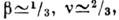 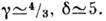Нек-рые эксперим. и теоретич. результаты для К. п. при 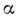=3 приведены в табл. 2.

Для ряда двумерных фазовых переходов К. п. удаётся вычислить точно, напр. в Изинга моделях и 8-вершинной, а также в ХУ-модели (см. Двумерные решёточные модели ).В модели Изинга К. п. универсальны:

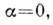
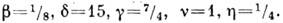В 8-вершинной

и XY-моделях, а также в нек-рых других К. п. неуниверсальны (зависят от параметров взаимодействия), что связано с существованием флуктуирующих величин с размерностями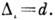

Литература по критическим показателям (критическим индексам)

Паташинский А. 3., Покровский В. Л., Флуктуационная теория фазовых переходов, 2 изд., М., 1982.

М. В. Фейгельман

к библиотеке к оглавлению FAQ по эфирной физике ТОЭЭ ТЭЦ ТПОИ ТИ

Знаете ли Вы, что низкочастотные электромагнитные волны частотой менее 100 КГц коренным образом отличаются от более высоких частот падением скорости электромагнитных волн пропорционально корню квадратному их частоты от 300 тысяч кмилометров в секунду при 100 кГц до примерно 7 тыс км/с при 50 Гц.

НОВОСТИ ФОРУМА

Рыцари теории эфира