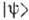системы,
к-рый удовлетворяет Шрёдингера ур-ниюГамильтониан (оператор Гамильтона) - квантовомеханич. оператор, соответствующий Гамильтона функции в классич. механике и определяющий эволюцию квантовой системы. В Шрёдинеера
представлении эта эволюция описывается зависимостью от времени вектора
состояния 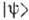системы,
к-рый удовлетворяет Шрёдингера ур-нию
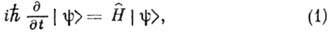
где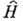 
-
гамильтониан. Если классич. функция Гамильтона не зависит явно от времени, то
она является интегралом движения и значение её совпадает с энергией системы.
Соответственно Г. системы в этом случае является оператором энергии. Ур-ние
(1) при этом имеет частные решения в виде стационарных состояний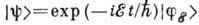 
, где вектор состояния 
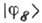не зависит от времени
и является собств. вектором Г., соответствующим значению энергии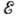 
:
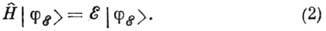
Ур-ние (2) определяет спектр
энергии системы.
Оператор производной по
времени физ. величины f также выражается через коммутатор Г. системы
с оператором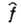 
данной физ. величины:
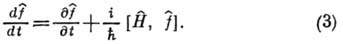
Ур-ние (3) используется
для описания эволюции системы в Гейзенберга представлении. Оно является
квантовомеханич. аналогом ур-ния для классич. функции f, зависящей от координат
qk и импульсов pk системы:
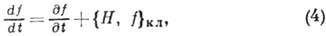
где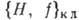 
- классич. скобка Пуассона,
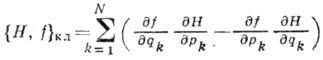
(N - число степеней
свободы системы). Сравнение ф-л (3) и (4) показывает, что в классич. пределе
коммутатор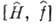 
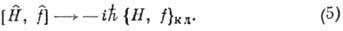должен переходить в 
.
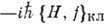Аналогичные соотношения
должны выполняться для коммутаторов операторов, соответствующих и др. классич.
физ. величинам. В согласии с этим Г. физ. системы получается из классич. функции
Гамильтона заменой классич. координат и импульсов частиц на соответствующие
операторы, подчиняющиеся коммутац. соотношениям. При этом возникает неоднозначность
в последовательности записи некоммутирующих операторов в выражениях, отвечающих
произведению классич. величин, к-рая устраняется симметризацией этих выражений,
напр. qi рi заменяется на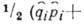
).
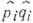Приведём Г. для простейших
систем:
а) частица массы т во
внеш. потенц. поле V(x, у, z):
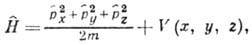
где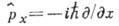 
и т. д.;
б)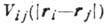 
система n частиц с парным взаимодействием
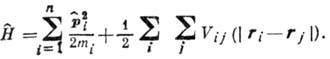
Аналогично в квантовой
теории взаимодействующих полей (т. е. в динамич. системах с бесконечным числом
степеней свободы) Г. системы получается из классич. гамильтоновой функции полей
заменой классич. величин (напр., амплитуд нормальных колебаний) соответствующими
операторами. Возникающая при этом неопределённость в порядке записи произведений
некоммутирующих операторов позволяет выбрать такую последовательность (т. н.
нормальное произведение ),к-рая естеств. образом определяет физ. вакуум
системы (см. Квантовая теория поля).
Если физ. величина f
не зависит явно от времени (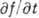
=0),
то условием её сохранения, согласно (3), является обращение в нуль коммутатора
оператора этой величины с Г. системы, 
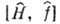=0,
т. е. условие одновременной измеримости данной величины и энергии системы.
Если Г. системы обладает
к--л. симметрией, то оператор, осуществляющий преобразования симметрии, коммутирует
с Г. Соответственно этому каждой симметрии Г. отвечает закон сохранения определённой
величины (см. Нетер теорема). Так, симметрии Г. относительно сдвигов
и поворотов системы в пространстве соответствуют законы сохранения импульса
и момента импульса системы, симметрии Г. относительно отражения координат частиц
- сохранение пространственной чётности системы и т. д. Симметрия Г. приводит,
как правило, к вырождению уровней энергии.
Поскольку Г. отвечает физ. величине (функции Гамильтона или энергии), он является эрмитовым оператором. Эрмитовость Г. обеспечивает сохранение нормы вектора состояния (т. е. полной вероятности). Однако для описания процессов с поглощением частиц (напр., процессов рассеяния адронов на ядрах) могут быть использованы комплексные потенциалы, соответствующие неэрмитовым Г. (см. Оптическая модель ядра).
С. С. Герштейн
Когда тот или иной физик использует понятие "физический вакуум", он либо не понимает абсурдности этого термина, либо лукавит, являясь скрытым или явным приверженцем релятивистской идеологии.
Понять абсурдность этого понятия легче всего обратившись к истокам его возникновения. Рождено оно было Полем Дираком в 1930-х, когда стало ясно, что отрицание эфира в чистом виде, как это делал великий математик, но посредственный физик Анри Пуанкаре, уже нельзя. Слишком много фактов противоречит этому.
Для защиты релятивизма Поль Дирак ввел афизическое и алогичное понятие отрицательной энергии, а затем и существование "моря" двух компенсирующих друг друга энергий в вакууме - положительной и отрицательной, а также "моря" компенсирующих друг друга частиц - виртуальных (то есть кажущихся) электронов и позитронов в вакууме.
Однако такая постановка является внутренне противоречивой (виртуальные частицы ненаблюдаемы и их по произволу можно считать в одном случае отсутствующими, а в другом - присутствующими) и противоречащей релятивизму (то есть отрицанию эфира, так как при наличии таких частиц в вакууме релятивизм уже просто невозможен). Подробнее читайте в FAQ по эфирной физике.
|
|
 |
