A. K. T. Assis*, M. C. D. Neves
Instituto de Física “Gleb Wataghin” Departamento de Física
Universidade Estadual de Campinas Universidade Estadual de Maringá
13083-970 Campinas, São Paulo, Brasil 87020-900 Maringá, PR, Brasil
Full text with appendixes in pdf-file
We present the history of estimates of the temperature of intergalactic space. We begin with the works of Guillaume and Eddington on the temperature of interstellar space due to starlight be-longing to our Milky Way galaxy. Then we discuss works relating to cosmic radiation, concen-trating on Regener and Nernst. We also discuss Finlay-Freundlich’s and Max Born’s important research on this topic. Finally, we present the work of Gamow and collaborators. We show that the models based on a Universe in dynamical equilibrium without expansion predicted the 2.7 K temperature prior to and better than models based on the Big Bang.
PACS: 98.70.Vc Background radiations 98.80.-k Cosmology
98.80.Bp Origin and formation of the Universe
Key Words: Cosmic background radiation, temperature of intergalactic space, blackbody radia-tion
In 1965 Penzias and Wilson discovered the Cosmic Background Radiation (CBR) utilizing a horn reflector antenna built to study radio astronomy (Penzias and Wilson 1965). They found a temperature of 3.5 ± 1.0 K observing background radiation at 7.3 cm wavelength. This was soon interpreted as a relic of the hot Big Bang with a blackbody spectrum (Dicke et al. 1965). The find-ing was considered a proof of the standard cosmological model of the Universe based on the expansion on the Universe (the Big Bang), which had predicted this tem-perature with the works of Gamow and collaborators.
In this paper we show that other models of a Uni-verse in dynamical equilibrium without expansion had predicted this temperature prior to Gamow. Moreover, we show that Gamow’s own predictions were worse than these previous ones.
Before beginning let us list briefly some important historical information which help to understand the findings. Stefan found experimentally in 1879 that the total bolometric flux of radiation F emitted by a black body at a temperature T is given by F = sT 4 , where s is now called Stefan-Boltzmann’s constant (5.67 ´ 10-8 Wm-2 K -4 ). The theoretical derivation of this expression was obtained by Boltzmann in 1884. In 1924 Hubble es-tablished that the nebulae are stellar systems outside the Milky Way. In 1929 he obtained the famous redshift-distance law.
The earliest estimation of a temperature of “space” known to us is that of Guillaume (1896). It was published in 1896, prior to Gamow’s birth (1904). Here we quote from this paper (English translation by C. Roy Keys):
“Captain Abney has recently determined the ratio of the light from the starry sky to that of the full Moon. It turns out to be 1/44, after reductions for the oblique-ness of the rays relative to the surface, and for atmos-pheric absorption. Doubling this for both hemispheres, and adopting 1/600000 as the ratio of the light in-tensity of the Moon to that of the Sun (a rough average of the measurements by Wollaston, Douguer and Zöllner), we find that the Sun showers us with 15,200,000 time more vibratory energy than all the stars combined. The increase in temperature of an iso-lated body in space subject only to the action of the stars will be equal to the quotient of the increase of tempera-ture due to the Sun on the Earth’s orbit divided by the fourth root of 15,200,000, or about 60. Moreover, this number should be regarded as a minimum, as the measurements of Captain Abney taken in South Kensington may have been distorted by some foreign source of light. We conclude that the radiation of the stars alone would maintain the test particle we suppose might have been placed at different points in the sky at a temperature of 338/60 = 5.6 abs. = 207º.4 centi-grade. We must not conclude that the radiation of the stars raises the temperature of the celestial bodies to 5 or 6 degrees. If the star in question already has a tempera-ture that is very different from absolute zero, its loss of heat is much greater. We will find the increase of temperature due to the radiation of the stars by calculat-ing the loss using Stefan’s law. In this way we find that for the Earth, the temperature increase due to the radiation of the stars is less than one hundred-thousandth of a degree. Furthermore, this figure should be regarded as an upper limit on the effect we seek to evaluate.”
Of course, Guillaume’s estimation of a 5-6 K blackbody temperature may not have been the earliest one, as Ste-fan’s law had been known since 1879. Moreover, it is restricted to the effect due to the stars belonging to our own galaxy.
We now quote from Eddington’s book, The Internal Constitution of the Stars (1988), published in 1926. The last chapter of this book is called “Diffuse Matter in Space” and begins discussing “The Temperature of Space:”
Chapter XIII
DIFFUSE MATTER IN SPACE
The Temperature of Space.
256.
The total light received by us from the stars is es-timated to be equivalent to about 1000 stars of the first magnitude. Allowing an average correction to reduce visual to bolometric magnitude for stars of types other than F and G, the heat received from the stars may be taken to correspond to 2000 stars of apparent bolo-metric magnitude 1.0. We shall first calculate the en-ergy-density of this radiation.A star of absolute bolometric magnitude 1.0 radiates 36.3 times as much energy as the sun or 1.37
´1035 ergs per sec. This gives 115. ´ 10-5 ergs per sq. cm. per sec. over a sphere of 10 parsecs (3.08 ´ 1019 cm.) ra-dius. The corresponding energy-density is obtained by dividing by the velocity of propagation and amounts to 3.83 ´ 10-16 ergs per cu. cm. At 10 parsecs distance the apparent magnitude is equal to the absolute magni-tude; hence the energy-density 3.83
´ 10-16 corre-sponds to apparent bolometric magnitude 1.0.
Accordingly the total radiation of the stars has an en-ergy-density
2000
´ 3.83 ´ 10-16 = 7.67 ´ 10-13 ergs / cm3 .By the formula E = sT 4 the effective temperature corresponding to this density is
3º.18
absolute.In a region of space not in the neighbourhood of any star this constitutes the whole field of radiation, and a black body, e. g. a black bulb thermometer, will there take up a temperature of
3º.18 so that its emission may balance the radiation falling on it and absorbed by it. This is sometimes called the ‘temperature of in-terstellar space.’One important aspect to emphasize here is that Ed-dington’s estimation of a temperature of 3.18 K was not the first one, as Guillaume had obtained a similar figure by 30 years earlier. Although Eddington did not quote Guillaume or any other author, it is clear that he was here following someone’s else derivation. This is indicated by the sentences “The total light received by us from the stars is estimated [by whom?] to be...” and “This is sometimes called [by whom?] the ‘temperature of inter-stellar space.’ “ These sentences show that others had also arrived at this result. It is very probable that in the fifty years between Stefan’s law (1879) and Eddington’s book (1926) others arrived at the same conclusion independent of Guillaume’s work (1896).
Another point to bear in mind is that Eddington and Guillaume were discussing the temperature of interstellar space due to fixed stars belonging to our own galaxy, and not of intergalactic space. Remember that Hubble only established the existence of external galaxies beyond doubt in 1924.
Cosmic rays were discovered in 1912 by V. F. Hess (Rossi 1964). He made a balloon flight and observed that a charged electroscope would discharge faster at high alti-tudes than at the sea level, contrary to expectations. This discharge is due to the ionization of the air, which was shown to increase with altitude. It was known that radia-tion emitted by radioactive substances ionized the air, and Hess’s measurements showed that the radiation respon-sible for the natural ionization of air entered the atmos-phere from above, and not from the ground.
In 1928 R. A. Millikan and Cameron (1928) found that the total energy of cosmic rays at the top of the atmos-phere was one-tenth of that due to starlight and heat. In 1933 E. Regener (1933) concluded that both energy fluxes should have essentially the same value. This is a very important result with far reaching cosmological implications: It indicates that the energy density of star-light due to our own galaxy is in equilibrium with the cosmic radiation, which for the most part is of extragalac-tic origin. It has always been difficult to know exactly the origin of the cosmic rays, but the fact that a major part of its components originated outside our galaxy was inferred from another measurement of Millikan and Cameron
Page 80
APEIRON Vol. 2 Nr. 3 July 1995(1928). In this work they showed that the intensity of the radiation coming from the plane of the Milky Way was the same as that coming from a plane normal to it. This isotropy clearly indicated an extragalactic origin.
Regener’s work in general has been described briefly by Rossi (1964) as follows:
In the late 1920s and early 1930s the technique of self-recording electroscopes carried by ballons into the highest layers of the atmosphere or sunk to great depths under water was brought to an unprecedented degree of perfection by the German physicist Erich Regener and his group. To these scientists we owe some of the most accurate measurements ever made of cosmic-ray ion-zation as a function of altitude and depth.
In his work of 1933, Regener says the following (we are here replacing the term Ultrastrahlung - ultraradiation - which Regener and others utilized at that time by the expression “cosmic radiation,” as this radiation is called nowadays):
However, the density of energy produced by cosmic rays, which is nearly equal to the density of light and heat emitted by the fixed stars, is very interesting from an astrophysical point of view. A celestial body with the necessary dimensions to absorb the cosmic rays—in case of a density of 1, a body with a diameter of several meters (5 meters of water absorb
109 of the cosmic rays)—will be heated by cosmic rays. The increase in temperature will be proportional to the energy of ab-sorbed cosmic rays (SU ) and the surface (O). The temperature of the body will increase until the heat it emits—in case of black body radiation s ×T 4 × O — reaches the same value. We then obtain a final tem-perature of T = 4 SU s . Substituting numerical values we obtain 2.8 KThis, according to Regener (1933), would be the tem-perature characteristic of intergalactic space, since in this region the light and heat from any galaxy would be neg-ligible.
The work of Regener was discussed by the famous physicist Walther Nernst (1864-1941) who received the Nobel prize for chemistry in 1920 for his third law of t hermodynamics (1906). By 1912 Nernst had developed the idea of an Universe in a stationary state. He expressed this idea in simple terms in 1928: “The Universe is in a stationary condition, that is, the present fixed stars cool continually and new ones are being formed” (Nernst 1928). In 1937 he developed this model and proposed a tired light explanation of the cosmological redshift, namely, the absorption of radiation by the luminiferous ether, decreasing the energy and frequency of galactic light (Nernst 1937). This would not be due to a Doppler
effect according to Nernst. In this work Nernst also mentions Regener’s important paper discussed above.
The following year Nernst (1938) published another paper discussing the radiation temperature in the Uni-verse. Here he arrived at a temperature in intergalactic space as 0.75 K. Once more he discusses Regener’s work and asserts that the cosmological redshift is not due to a Doppler effect.
In the works of Eddington, Regener, Nernst and others to follow, it is important to stress the utilization of Stefan-Boltzmann’s law, which is characteristic of a black body radiation. Another point to be noted is that the en-ergy densities of these radiations (due to star light and cosmic rays, for instance) have been measured to have the same value, indicating a situation of dynamical equilib-rium. Sciama describes this situation as follows (Sciama 1971):
The cosmic ray flux almost certainly fills the Milky Way, and corresponds to an energy density in interstel-lar space of about
1 eVcm-3 (10-12 erg cm-3 ). This is comparable with the energy density of starlight, the turbulent kinetic energy density of the interstellar gas and, as we shall see later, the energy density of the interstellar magnetic field. This is the basis of our statement that the cosmic rays are dynamically impor-tant. They constitute a relativistic gas whose energy and pressure cannot be ignored. The near-equality of the various energy densities is probably no accident, but despite many attempts a full understanding of it has not yet been achieved.And again on p. 185, after mentioning Penzias and Wilson’s discovery of a blackbody radiation of 3 K:
From a laboratory point of view 3 K is a very low temperature. Indeed to measure it the microwave ob-servers had to use a reference terminal im
mersed in liquid helium. Nevertheless from an astrophysical point of view 3º K is a very high temperature. A un iversal black body radiation field at this temperature would contribute an energy density everywhere of 1 eVcm-3 . As we saw in chapter 2 [p. 25] this is just the energy density in our Galaxy of the various modes of interstellar excitation—starlight, cosmic rays, mag-netic fields and turbulent gas clouds. So even in our Galaxy the cosmological background radiation would be for many purposes as important as the well-known energy modes of local origin.We would like to make two remarks here. The first is that the main part of the cosmic radiation may have an extragalactic origin (see the comment on the work of Millikan and Cameron above), as may the magnetic fields which fill all space. If this is the case, then three extraga-lactic modes of excitation (the cosmic ray flux, magnetic fields and the CBR) would be in thermal equilibrium with one another and with energy fields generated inside our own galaxy, such as starlight and turbulent gas clouds. The easiest way to understand this fact is to con-clude that the Universe as a whole is in a state of dynami-cal equilibrium.
Here we would like to mention briefly the work of Herzberg in 1941 (based on observations made by A. McKellar) discussing cyanogen measurements in inter-stellar space. Herzberg found a temperature of 2.3 K characterizing the observed degree of excitation of the CN molecules if they were in equilibrium in a heat bath (Herzberg):
The observation that in interstellar space only the very lowest rotational levels of
CH, CH+, and CN are populated is readily explained by the depopulation of the higher levels by emission of the far infrared rotation spectrum (see p. 43) and by the lack of excitation to these levels by collisions or radiation. The intensity of the rotation spectrum of CN is much smaller than that of CH or CH+ on account of the smaller dipole moment as well as the smaller frequency [due to the factor n 4 in (I, 48)]. That is why lines from the sec-ond lowest level (K = 1) have been observed for CN. From the intensity ratio of the lines with K = 0 and K = 1, a rotational temperature of 2.3 K follows, which has of course only a very restricted meaning.Obviously there is a great meaning in this result, al-though it was not recognized by Herzberg. This is dis-cussed by Sciama (1971). It should only be stressed that once more, this result was not obtained utilizing the Big Bang cosmology.
In 1953-4 Finlay-Freundlich (1953, 1954a,b)proposed a tired light model to explain the redshift of solar lines and some anomalous redshifts of several stars, as well as the cosmological redshift. He proposed a redshift pro-portional to the fourth power of the temperature, and his work was further analysed by Max Born (1953, 1954). His formula is as follows: Dn / n = - AT 4 l, where Dn is the change in frequency of the line, n its original fre-quency, A is a constant, T the temperature of the radia-tion field and l the length of path traversed through the radiation field. What matters to us here is his discussion (1954b) of the cosmological redshift:
§ 6. The Cosmological Red Shift
The fundamental character of the effect under consid-eration raises, necessarily, the question whether it might not also be the cause of the cosmological red shift which hitherto has been interpreted as a Doppler effect. In this case, the influence of the factor l in formula (1) is given explicitly from observations. The observed red shift
Dl / l increases for every million parsec ( = 3 ´ 1024 cm ) by 0.8 ´ 10-3 which corresponds to avelocity increase of 500 km/sec when interpreted as a Doppler effect. An increase by 10 km/sec—
|
corresponding to the red |
shift in a |
B2 |
star |
with |
|
TB = 20000 K —would |
correspond |
to |
a |
path |
lS = 1.2 ´1023 cm .
As far as the mean temperature
TS of intergalactic space is concerned, apart from the knowledge that it must be near the absolute zero, no reliable information is available. If we may interpret the cosmological red shift in the same way as the stellar red shifts, the fol-lowing equation should hold:T
“Equation (3) shows that the value of TS obtained in this way does not depend strongly on the choice of lB .
Taking for lB the two extreme values 107 cm and
109 cm , we get the following two reasonable values
TS = 1.9K and TS = 6.0K .
In a recent paper Gamow (1953) [Gamow, G., 1953,
Dan. Acad. Math.-Phys. Section, 27, No. 10] derives a value for TS of 7 K from thermodynami-cal considerations assuming a mean density of matter in space of 10-30 g / cm3 .One may have, therefore, to envisage that the cosmo-logical red shift is not due to an expanding Universe, but to a loss of energy which light suffers in the im-mense lengths of space it has to traverse coming from the most distant star systems. That intergalactic space is not completely empty is indicated by Stebbins and Whitford’s discovery (1948) [Stebbins, J., and Whit-ford, A. E., 1948,
Ap. J., 108, 413] that the cosmo-logical red shift is accompanied by a parallel unac-countable excess reddening. Thus the light must be ex-posed to some kind of interaction with matter and radiation in intergalactic space.The main points to emphasize here are that Finlay-Freundlich proposed an alternative to the Doppler in-terpretation of the cosmological redshift and arrived at 1.9 K < T < 6.0 K for the temperature of intergalactic space. This is quite remarkable.
It is important to quote here Max Born (1954) when discussing Finlay-Freundlich’s proposal that this new ef-fect might be due to a photon-photon interaction, namely :
An effect like this is of course not in agreement with current theory. It has, however, an attractive conse-quence. A simple application of the conservation laws of energy and momentum shows that a collision of this kind is only possible if a pair of particles with opposite photons their frequency is of the order of radar waves momenta is created. The energy of one of these is
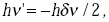

(for the sun n'~ 2 ´ 109 sec-1, l'~ 15cm ). Thus the red-shift is linked to radio-astronomy.
We need only remember here the work of Penzias and Wilson 11 years later with a horn antenna built to study radio waves which found the CBR with a charac-teristic wavelength of 7 cm... This must be considered a highly successful prediction by Max Born!
As we have seen, Finlay-Freundlich (1954b) men-tioned that Gamow had derived the value of 7 K for in-tergalactic space in 1953. Prior to this work we could only find two other papers where there was a prediction of this temperature by Gamow’s collaborators Alpher and Her-man (1948, 1949). In the first of these works they said: “The temperature of the gas at the time of condensation was 600 K., and the temperature in the Universe at the present time is found to be about 5 K. We hope to pub-lish the details of these calculations in the near future.”
In the second of these works, where the present the details of these calculations, they said the following (our emphasis in bold):
In accordance with eq. (4) [
rr rm-4 / 3 = cons tant ], the specification of rm '', rm ', and rr ' fixes the present density of radiation, rr '' . In fact, we find that the value of rr '' consistent with eq. (4) isr
rwhich corresponds to a temperature now of the order 5 K
. This mean temperature for the Universe is to be interpreted as the background temperature which would result from the universal expansion alone.However, the thermal energy resulting from the nuclear energy production in stars would increase this value.”
From this it is evident that their prediction in 1948 was T » 5K and in 1949 they obtained a temperature greater than 5 K, although close to this value.
The only other prediction of this temperature by Gamow known to us prior to Penzias and Wilson dis-covery (beyond that of 7 K in 1953) was published by Gamow (1961) in his book The Creation of the Universe. The first edition of this book is from 1952, and here we quote from the revised edition of 1961, only four years before Penzias and Wilson. In this book there is only one place where he discusses the temperature of the Uni-verse, namely [21, p. 42, our emphasis in bold]:
The relation previously stated between the value of Hubble’s constant and the mean density of the Uni-verse permits us to derive a simple expression giving us the temperature during the early stages of ex pansion as the function of the time counted from the moment of maximum compression. Expressing that time in sec-onds and the temperature in degrees (see Appendix, pages 142-143), we have:

Thus when the Universe was 1 second old, 1 year old, and 1 million year old, its temperatures were 15 bil-lion, 3 million, and 3 thousand degrees absolute, re-spectively. Inserting the present age of the
univserse (t = 1017 sec ) into that formula, we find
Tpresent = 50 degrees absolute
which is in reasonable agreement with the actual temperature of interstellar space. Yes, our Universe took some time to cool from the blistering heat of its early days to the freezing cold of today!
We discuss these predictions by Gamow and collabora-tors below.
In most textbooks nowadays we see the statement that Gamow and collaborators predicted the 2.7 K tempera-ture prior to Penzias and Wilson, while the steady-state theory of Hoyle, Narlikar and Gold did not predict this temperatu re. Therefore the correct prediction of the 2.7 K is hailed as one of the strongest arguments in favour of the Big Bang. However, these two models have one very important aspect in common: both accept the interpreta-tion of the cosmological redshift as being due to a Dop-pler effect, which means that both models accept the ex-pansion of the Universe.
But there is a third model of the Universe which has been developed in this century by several scientists in-cluding Nernst, Finlay-Freundlich, Max Born and Louis de Broglie (1966). It is based on a Universe in dynamical equilibrium without expansion and without continuous creation of matter. We reviewed this subject in earlier pa-pers (Assis 1992, 1993). Although it is not considered by almost any textbook dealing with cosmology nowadays, this third model proves to be the most important one of all of them.
In order to understand how the textbooks could ne-glect equilibrium cosmology so completely, it is worth-while to quote a letter sent by Gamow to Arno Penzias, in 1965 after Penzias and Wilson’s discovery (curiously the letter was dated 1963...). This letter was reproduced in Penzias’s article (1972), from which we quote:
Thank you for sending me your paper on 3 K radia-tion. It is very nicely written except that “early his-tory”is not “quite complete”. The theory of, what is now known, as, “primeval fireball”, was first devel-oped by me in 1946 (Phys. Rev. 70 , 572, 1946; 74, 505, 1948; Nature 162, 680, 1948). The predict
ion of the numerical value of the present (residual) tem-perature could be found in Alpher & Hermann’s paper (Phys. Rev. 75, 1093, 1949) who estimate it as 5 K, and in my paper (KongDansk. Ved. Sels 27 nº 10, 1953) with the estimate of 7 K. Even in myAPEIRON Vol. 2 Nr. 3 July 1995
Page 83popular book
Creation of the Universe (Viking 1952) you can find (on p. 42) the formulaTt K = . 1 5 1010 1 2 . / / , and the upper limit of 50 K. Thus, you see the world did not start with
almighty Dicke.
Sincerely, G. Gamow
This letter, as we have seen, does not correspond to the true facts. Gamow, in the revised edition of his book of 1952, published in 1961, calculated a temperature.
Thus, in this work Gamow did not estimate an upper limit of 50 K. The need for Gamow to convince everybody that he had predicted correctly, and before everyone else, the temperature of the cosmic background radiation is evident from another part of Penzias’s paper (1972):
It is beyond the scope of this contribution to weigh the various theoretical explanations of the 3 K. Still the unique claim of the hot evolving Universe theory is that it predicted the background radiation before the fact. At the 4th “Texas” Symposium on Relativistic Astrophysics, George Gamow was the chairman of the session on Microwave Background Radiation. He
ended his remarks with a comment which, to the best of my recollection, went, “If I lose a nickel, and someone finds a nickel, I can’t prove that it’s my nickel.
Still, I lost a nickel just where they found one.” The applause was loud and long.
As we have seen in this paper, Gamow and collaborators obtained from T ” 5 K to T = 50 K in monotonic order (5 K, . 5 K, 7 K and 50 K)... These are quite poor predictions compared with Guillaume, Eddington, Regener and Nernst, McKellar and Herzberg, Finlay-Freundlich and Max Born, who arrived at, respectively: 5 K < T < 6 K, T = 3.1 K, T = 2.8 K, T = 2.3 K, 1.9 K <
T < 6.0 K! All of these authors obtained these values from measurement and or theoretical calculations, but none of them utilized the Big Bang. This means that the discovery of Penzias and Wilson cannot be considered decisive evidence in favour of the Big Bang. Quite the contrary, as the models of a Universe in dynamical equilibrium predicted its value before Gamow and with better
accuracy. And not only this, Max Born also predicted that the cosmological redshift and the cosmic background radiation should be related with radio astronomy eleven years before the discovery of the CBR by Penzias and Wilson utilizing a horn reflector antenna built to study radio emissions!
Our conclusion is that the discovery of the CBR by Penzias and Wilson is a decisive factor in favour of a Universe in dynamical equilibrium, and against models of an expanding Universe, such as the Big Bang and the steady-state.
Acknowledgments
The authors with to thank Dr. Anthony L. Peratt for bringing Guillaume’s paper to their attention. A.K.T.A. wishes to thank CNPq, FAPESP and FAEP for financial support in the past few years.
|
|