© Copyright - Karim A. Khaidarov, 2016
Светлой памяти самых близких мне людей
- супруги Лидии и дочери Анастасии посвящаю.
Настоящий курс подготовлен для широкого круга людей, имеющих дефицит структурного мышления, - а к таковым, к сожалению, относится подавляющая часть моих современников, - с целью помочь им преодолеть этот дефицит и приобрести некоторые навыки адекватного мышления путем освоения инструмента теории иерархий в познании бесконечно сложного мира, в котором мы живем.
Мышление современных людей можно отнести всего-навсего к трем исходным типам:
Кроме трёх основных типов существуют и их комбинации, из которых можно выделить наиболее распространенный - комбинационно-имитационный тип, представляющий заимствование, мимикрию под чужие шаблоны, их комбинацию и имитацию; для таких людей главным вопросом является: «Что играть?», см. Йохан Хейзинга, Homo ludens. Фатальной проблемой такого типа мышления и поведения является необратимо нарастающая асоциализация среды с последующим ее системным разрушением.
Три основных типа соответствуют трем основным исходным видам рода человеческого Homo vulgaris: человека - «растительного» с морфологическим, чувственно-образным типом мышления, «травоядного» человека с синтаксическим типом мышления, человека - «хищника» с прагматическим типом мышления. Эти три типа мышления достались нам от наших животных предков и, к сожалению, ни один из них, включая их различные комбинации, не удовлетворяет новым требованиям к выживанию, вставшим сегодня перед человечеством. Теория иерархий является одним из тех инструментов познания, которые позволяют выйти человеку из порочного круга животного восприятия мира.
Для четкого понимания понятия иерархии необходимо определить его родовые определения — более общие понятия, на которых оно строится.
Термин «иерархия» является термином теории графов. Сама теория графов есть графоаналитическое представление логики и во многом определяет сущность таких наук, как общая теория систем, общая теория сетей, общая и дискретная топология.
Основным объектом теории графов является
Исследуемые объекты представляются как вершины, или узлы графа, а связи — как «дуги», или рёбра [1]. Для разных областей применения виды графов могут различаться направленностью, ограничениями на количество связей и дополнительными данными о вершинах или рёбрах.
Важнейшей разновидностью графа является дерево:
Понятие иерархии в общем логическом значении есть эквивалент понятия субординации, порядка подчиненности объектов любой системы между собой. Свойство иерархии — направленность связей («дуг») между узлами (объектами), выражает наличие ранговых отношений между узлами (объектами), описываемых некоей ранговой оценкой: подчиняющий - подчиненный, больше — меньше, содержит — является частью, причина — следствие, раньше — позже и т. п. В отличие от простого дерева, в котором можно произвольно принять корнем графа (корневой вершиной) любой узел и строить от него пути, в иерархии может быть только один ее узел (элемент, объект), являющийся корневой вершиной, так как отношения подчиненности определены независимо от воли стороннего наблюдателя, исследователя. При вмешательстве, изменении направлений связей в иерархии, она разрушается до простого дерева.
Понятие иерархии является основополагающим в любой науке, но прежде всего в логике, что, как правило, остается в тени, вне рассмотрения. Последнее приводит к тому, что используемая людьми логика часто является неадекватной, не приводящей к истине как основной цели логических построений.
Кроме того, сам физический мир, в котором мы живем, имеет иерархическую природу, но его иерархической реальности обыватель обычно не видит, а если видит, то не понимает. Всё в реальном мире пропитано иерархиями, построено на различных видах иерархий. Мир представляет собой вселенскую Матрону и состоит из иерархически вложенных друг в друга разнообразных объектов и процессов, которые есть ничто иное, как элементы различных систем, в свою очередь являющихся элементами более крупных систем, представляя собой иерархические системы более высоких рангов, порядков.
Любая система есть некая иерархия ее элементов и/или свойств.
Само физическое пространство, в котором мы живем, - это иерархия его свойств: местоположения точки, протяженности линии, площади поверхности, объёма пространства...
То же самое в общественных и технических системах.
Поэтому без владения понятийным аппаратом теории иерархий адекватное мышление, логика — просто невозможны, ибо без учета иерархии в рассуждениях легко происходит подмена, возникает путаница в объектах разных рангов.
К великому прискорбию надо признать, что вследствие исключения даже плоско-примитивной формальной логики, как предмета из системы обучения (исключена из программ обучения в России в 1918 г. постановлением Наркомпроса, А.В. Луначарским наряду с историей, латынью и греческим), подавляющая часть людей не владеет элементарными основами адекватного логического мышления, а пользуется той бытовой логикой, которая им досталась из бытового окружения и собственного детско-первобытного опыта. Да и сама формальная логика, не пересматривавшаяся со времен Аристотеля, не имеет адекватного аппарата работы с иерархиями. Именно поэтому в ней возникает масса парадоксов — индикаторов ее неадекватности. Ошибка парадокса в отличие от паралогизмов и софизмов не обнаружима в современной формальной логике — плоской логике аристотелевского типа из-за отсутствия аппарата идентификации рангов иерархии объектов.
В формальной логике различают такие разновидности логических парадоксов, как апория и антиномия.
Апория характеризуется наличием аргумента, противоречащего очевидному, общепринятому мнению, здравому смыслу. Антиномия — наличием двух противоречащих друг другу, якобы одинаково доказуемых суждений.
Это, к примеру, 40 апорий Зенона, Эпименидов парадокс лжеца, тролль-парадокс Бертрана Рассела к логической системе Готлоба Фреге. Все эти парадоксы, то есть приведение к противоречию или абсурду, являются рассуждениями, нарушающими иерархию логических объектов, то есть совершающих незаметную для воспринимающего подмену понятий и уровней иерархии (математическую сумму сложения копеек выдают за количество рублей).
Ярким примером является сегодняшняя физика, где засилие математиков, не смыслящих и не мыслящих, уже по определению математики — чисто количественной науки, в физических качествах — размерностях и их иерархии, завело физику в глубокий кризис - тупик. Они без тени сомнения складывают метры и секунды, и получают свою абсурдную химеру пространства-времени, заставляя всех верить в эту чепуху.
Использование приёма парадоксальности сегодня является одним из важнейших инструментов мошенников разного толка, особенно эффективных, когда сам мошенник прекрасно знает о своей подмене и ее выгодных свойствах. Поэтому, когда вам говорят о парадоксе, прежде всего надо искать обман (преднамеренную ложь).
И в таких ситуациях знание основ теории иерархий — совершенно необходимо.
Теории иерархии, созданные У. Муром, К. Дэвисом, А. Маслоу в применении к социологии и психологии, частны, не научны и явно недостаточны для построения настоящей всеобъемлющей теории, которая могла бы быть инструментом познания — анализа и синтеза в любой науке. Попытки решить проблему иерархий в «теории измерений» А.И. Орлова, «теории лингвистической переменной» или «нечеткой логике» Лютфи Заде также не дают должного эффекта. Именно дефицит такого инструмента, который позволил бы решать логические задачи без возникновения парадоксов, понимать структуру, взаимоотношения внутри сложных систем, из которых состоит окружающий нас реальный физический мир, определил задачи настоящего курса.
В «теории измерений» А. И. Орлова не идет речь о важнейшем свойстве любых реальных объектов — их качестве. Отношения между объектами А. И. Орлов пытается выстроить на количественном отношении неравенства, ранжирования, называя это измерением. Однако, следует отметить, что измерение есть процесс определения некоторой меры объекта.
Для понимания процессов ранжирования и измерения определим термины, которых будем придерживаться (часто навязываемый оппонентами спор о «правильности» терминов не имеет смысла ибо во всяком языке существуют свои внутренние правила, на которые не может посягать иной язык. Яркий пример: булка — форма единицы хлебопродукта в русском языке; булка — девушка в болгарском языке).
Это аддитивность по отношению к самой себе и инвариантность относительно каких-либо эквивалентных математических преобразований, способов измерения. То есть, чтобы какую-либо оценку называть мерой, необходимо, чтобы эта оценка давала те же самые (то есть инвариантные) результаты в процессе измерения одного и того же объекта любым способом. Кроме того, любая перестановка объектов внутри измеряемой совокупности должна давать ту же самую меру каждого объекта и их совокупности. Данные условия установлены основоположниками теории меры: Готлибом Лейбницем в конце XVII века, а затем уточнены Анри Лебегом в начале ХХ века.
Эти условия однозначно приводят к понятию аддитивности, которое является неотъемлемым свойством любой меры. Поэтому без оной нет предмета измерения, и то, что проф. А.И. Орлов называет измерениями и их теорией есть нечто иное. Это иное — ранжирование объектов, которое еще не есть их мера, но лишь их упорядочение.
Отказ А.И. Орлова от аддитивности по-видимому был попыткой распространить понятие меры на качественные отношения, однако, следует констатировать, что он не удался, ибо категория качества в «теории измерения» А.И. Орлова отсутствует.
То же самое можно сказать и о теории Л. Заде, в которой он в условиях отсутствия однозначных количественных измерений и качества принятия решений попытался заменить логику и корректные измерения неким их суррогатом — введением оценки, ансамбля произвольных вероятностных мер, к которым применяются те же действия, что и к корректным мерам, и осуществляется попытка получения на основе этих действий корректных логических результатов. В некоторых случаях это получается, но в большинстве дает сбой.
Причина ошибок коллег заключается в том, что они смешивают качественное с количественным, не обращая внимания на их антагонистически различные свойства.
К примеру, картофель (качество) — есть картофель независомо от того, это одна клетка картофеля, клубень, килограмм или вагон. То же самое с любым другим объектом-свойством. К примеру, железо есть железо будь то атом или какой-либо объект из железа: техничекая деталь, железный метеорит, железный самородок, расплав железа.
Отличительной чертой качества являются: нижняя граница его существования, «атом качества», который определяется минимальным количеством, сохраняющим данное качество, и его верхняя граница (если она существует), которая также определяет критическое количество объекта, выше которого он теряет свое качество, но взамен приобретает иное, новое качество. Пример — капля жидкости, которая перестает быть каплей при превышении количества жидкости в ней, нарушающего силы поверхностного натяжения, формирующие каплю, масса делящегося химического элемента, например, плутония, перестает быть плутонием выше критической массы, за которой следует ядерный взрыв и образование новых химических элементов. Сами химические элементы меняют качество при любом изменении количества протонов в ядре, становясь иными элементами.
Таким образом, определенное качество может существовать только в определенных количественных границах.
Таким образом,
Важной особенностью иерархий является то, что существует два типа иерархий: качественные и количественные.
Между этими двумя типами есть принципиальная разница: качественная иерархия — необратима (рубль всегда не копейка), а количественная — обратима, то есть в ней возможно изменение ранга узла от текущего количества (дотаточно для оплаты или нет).
Давайте, рассмотрим эти условия в самом общем виде и определим условия возникновения, существования и потери качества, основополагающей категории в теории иерархий. Для этого надо определиться с базовыми понятиями теории информации (просьба не путать с теорией передачи информации Клода Шеннона, рассматривающей частный случай статистических свойств каналов связи).
Для правильного представления о понятиях качества и количества необходимо определиться с их областью определения, то есть наукой, в которой эти поняния являются наиболее общими (иерархически высшими, корневыми).
Такой наукой оказывается вовсе не математика и ее теория меры, а теория информации и подчиненная ей теория измерений, но не «теория измерений» Орлова, где отсутствует мера, а теория измерений, общая для метрологии, физики, информатики и других технических наук, где оперируют с реальными измерениями, реальными сигналами, реальной информацией, поступающей в измерительный прибор, систему, устройство, процесс, программу, где на основе этой информации производятся измерительные действия.
Любая информационная система состоит, как минимум, из трех элементов:
Информационные системы могут быть различных типов - уровней:
Существует два основных типа информации: данные и сигналы.
Как уже упоминалось ранее, любой процесс измерения / идентификации есть процесс принятия решений, позволяющий снять неопределенность в рамках используемой модели целевого объекта, причем неопределенность может быть двух основных типов:
При этом возможен переход от количества к качеству и наоборот.
Ключевым понятием в этом переходе являются понятия конечности и бесконечности.
В современной науке используется весьма узкое, пригодное лишь в математике, то есть количественных операций понятие конечности. В математике оно означает возможность получения однозначной меры, количества, содержащегося в объекте. Однако более общим понятием конечности является следующее.
Противоположным понятием конечности является бесконечность.
В современной науке используется весьма узкое, пригодное лишь в математике, то есть количественных вычислениях, понятие бесконечности, с практически выхолощенным до полного утрирования качественным и информационным содержанием.
На самом деле это понятие намного шире, выходит за рамки математики, ибо математика, как частный, технологический вариант логического механизма [Готлоб Фреге, 1892], манипулирует только с количеством, не зная качества.
Понятие бесконечности напрямую связано с переходом количества в качество, и этот переход заложен в изначальном определении бесконечности.
При этом необходимо различать два следующих типа бесконечностей.
Сами процессы идентификации качества и измерения количества есть информационные процессы происходящие в конкретном техническом устройстве или конкретной нервной системе. Поэтому понятие субъектной бесконечности носит частно-субъектный, конкретный характер при принятии решения, проявляющийся для каждого объекта индивидуально. Несмотря на последнее свойство сам переход от измеримости, конечности к неизмеримости, бесконечности носит объективный характер, ибо приводит к новому качеству, идентифицируемому со стороны внешних, независимых от производящего измерения объекта, других объектов и соответствующему объективно новому качеству в данной системе и физическом мире.
Для ясного понимания приведем простой технический пример (гуманитарии этот пример могут пропустить).
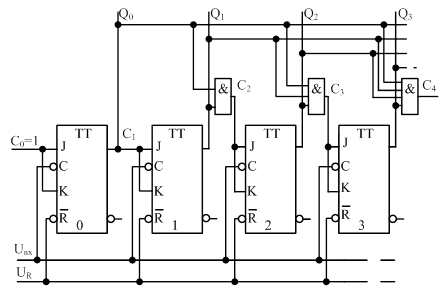
Пример 1. Переполнение счетчика. Имеется счетчик импульсов (n-разрядная, в данном случае, см. рис.1, n=4, логическая схема, наращивающая хранимую сумму идентифицированных входных сигналов на единицу (вход «1») всякий раз при поступлении на вход Uвх нового импульса).

Рис.1. Синхронный двоичный счетчик с переносом и сбросом.
Информационная ёмкость микросхемы — 2n = 16, то есть в ее памяти могут сохраняться числа от 0 до 2n-1. Сn выходов счетчика Q0... Q(n-1) в виде параллельного двоичного кода можно снять информацию о сумме (количестве) импульсов, поступивших на счетчик с момента его последнего обнуления специальным сигналом сброса UR. В случае, когда в памяти счетчика уже записано максимальное число, а на вход подается следующий импульс, ею вырабатывается так называемый сигнал переноса C4, то есть импульс, информирующий схему — потребитель информации о том, что произошло переполнение счетчика.
Таким образом, на выходе счетчика мы имеем два типа сигналов: количественный, о сумме поступивших импульсов, и качественный (логический) — о переполнении памяти счетчика.
Сигнал C4 представляет собой реализацию понятия бесконечности — неопределенно большого, неизмеримого количества. То есть для данного устройства — бесконечность — это любое число, большее емкости счетчика.
Такие числа полностью отвечают понятию бесконечности применительно к данному устройству.
Особенностью состояния переноса C4 является его необратимость, не позволяющая перейти от качества «перенос», «бесконечность» к качеству «конечное число», ибо даже подав сигнал на реверсный вход (для счетчика с реверсом) после возникновения сигнала переноса, в схеме невозможно восстановить правильное количество, так как неизвестно, какое количество импульсов было подано на вход после переполнения памяти, то есть после возникновения сигнала C4.
Пример 2. Деление на 0. Бесконечностью является и случай деления на 0 или слишком малое для данного устройства или вычислительного процесса число. В таких случаях в микросхемах и программах также предусмотрен специальный логический сигнал «деление на ноль», который имеет свойства бесконечности.
Таким образом понятие бесконечности может быть применено к конечным с точки зрения математики числам.
Пример 3. Целочисленное деление малого натурального числа на большое. То же самое и в отношении понятия бесконечно малого числа, которое в вычислительных устройствах появляется, если отношение, результат деления двух целых чисел составит величину 0 целых.
Можно привести и другие примеры из практики, которые показывают, что неопределенно большое число для данного устройства или процесса (программы) есть условная или физическая бесконечность. Условием является физическая емкость устройства или процесса, совершающего физическое измерение или математическое вычисление. При этом эта бесконечность не меняет своего качества быть бесконечностью при передаче информации другому, возможно более мощному, ёмкому устройству, ибо сам процесс измерения / вычисления происходит в первом устройстве, и ёмкость второго устройства не имеет никакого значения.
Пример 4. Переполнение памяти. Другое дело, если передается количественная информация, не помещающаяся в приемник. В этом случае информация о количестве теряется и мы снова имеем дело со случаем перехода количества в качество «бесконечность», неопределенно большое число.
Таким образом, бесконечность есть результат порогового перехода количества в новое качество, возникновение новых свойств — материально-физических или информационно-логических в состоянии системы, в которой происходит данный процесс. Порогом перехода являются физические качества системы, в которой происходит данный информационный процесс.
Здесь стоит отметить, что «старое качество» есть качество, которое атрибутивно, то есть по-определению связано с единицей количества, которым манипулируют в данном процессе. Об атрибутивности качества любому количеству, как правило, не думают или даже не ведают о нем. Именно поэтому в рассуждениях возникают парадоксы, когда, говоря школьным языком, «складывают коров, людей и трудодни», не понимая, что это есть подмена сущностей, сложение несовместимого.
Проблема физического качества рассмотрена, к примеру, в работе «Размерности физических величин», к которой отсылаю интересующегося читателя.
Для понимания последующего изложения отметим, что в связи с тем, что в реальном мире чаще всего мы имеем дело со сложными системами, характеризующимися тем, что в рамках теоретических моделей, которыми мы их представляем, а также по своей сущности сложных систем, они не имеют четких, простых границ.
Примеров таких проблем много:
На самом деле существование такой проблемы есть признак сложной системы. Причем сложность в данном случае является не результатом наличия большого количества элементов, но наличием неопределенности, отсутствия однозначной измеримости границ системы и/или её элементов.
В связи с этим, сложные качественные иерархии (сложные системы) имеют на границах (периферии) отношения, связи, свойственные количественным иерархиям. Кроме того, часто встречаются множественные иерархии — лес иерархий, а также вложенные системы иерархий — иерархии иерархий.
С понятием бесклонечности, качественного перехода тесно связано не только понятие уровня, порядка иерархии, но и понятие компоненты размерности, как новой независимой координаты, возникающей при таком переходе.
В силу несовершенства естественнного человеческого языка вместо «компонента размерности» используется слово «измерение», омонимичное понятию измерения, как процесса получения значения меры какой-либо физической величины, параметра или процесса. Для исключения неоднозначности постараемся избегать употребления слова «измерение» вместо «компонента размерности», а в тех случаях, когда это затруднительно, будем указывать значение слова в контексте.
Очень важные и часто употребляемые понятия дискретности и непрерывности требуют своего четкого определения, ибо иначе можно прийти к ложным построениям и выводам.
Таким образом, непрерывность есть одна из форм бесконечности, неопределенно большой сложности объекта. Это свойство непрерывности логически исключает ее распространение на заведомо простые, атомарные объекты. То есть атом — это всегда дискретный объект. Наличие непрерывности автоматически означает сложность объекта. Именно поэтому дискретность есть синоним простоты, а непрерывность — синоним сложности.
Данные понятия имеют большое значение в теории иерархий, и поэтому необходимо их рассмотреть хотя бы в общих чертах, а также определиться с терминологией.
Примерами нормальных иерархий являются ортогональные системы координат, Евклидово и физическое пространство, объем тела в пространстве — аналог объема иерархии.
Карим Хайдаров, Боровое, лето 2016
|
|