|
|
|
|
На вход системы передачи информации (СПИ) от источника информации подается совокупность сообщений, выбранных из ансамбля сообщений (рис. 1).
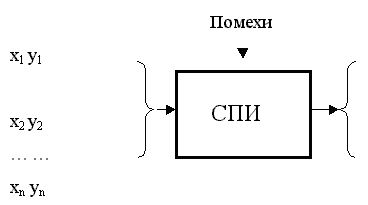
Ансамбль сообщений – множество возможных сообщений с их вероятностными характеристиками – {Х, р(х)}. При этом: Х={х1, х2,…, хm} – множество возможных сообщений источника; i = 1, 2,…, m, где m – объем алфавита; p(xi) – вероятности появления сообщений, причем p(xi) і 0 и поскольку вероятности сообщений представляют собой полную группу событий, то их суммарная вероятность равна единице
.
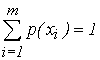Каждое сообщение несет в себе определенное количество информации. Определим количество информации, содержащееся в сообщении xi, выбранном из ансамбля сообщений источника {Х, р(х)}. Одним из параметров, характеризующих данное сообщение, является вероятность его появления – p(xi), поэтому естественно предположить, что количество информации I(xi) в сообщении xi является функцией p(xi). Вероятность появления двух независимых сообщений x1 и x2 равна произведению вероятностей p(x1, x2) = p(x1).p(x2), а содержащаяся в них информация должна обладать свойством аддитивности, т.е.:
I(x1, x2) = I(x1)+I(x2).
(1)Поэтому для оценки количества информации предложена логарифмическая мера:
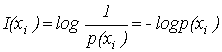. (2)
При этом наибольшее количество информации содержат наименее вероятные сообщения, а количество информации в сообщении о достоверном событии равно нулю. Т. к. все логарифмы пропорциональны, то выбор основания определяет единицу информации: logax = logbx/logba.
В зависимости от основания логарифма используют следующие единицы информации:
2 – [бит] (bynary digit – двоичная единица), используется при анализе ин-формационных процессов в ЭВМ и др. устройствах, функционирующих на основе двоичной системы счисления;
e – [нит] (natural digit – натуральная единица), используется в математических методах теории связи;
10 – [дит] (decimal digit – десятичная единица), используется при анализе процессов в приборах работающих с десятичной системой счисления.
Схожую меру другого иерархического уровня (комбинаторно-геометрического) - двоичный разряд часто путают с битом, считая, что байт (8 двоичных разрядов) = 8 битам, хотя это не так. (в двоичных разрядах не задана вероятность, а значит, не может быть определена мера от вероятности).
Среднее количество информации для всей совокупности сообщений можно получить путем усреднения по всем независимым событиям:
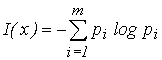. (3)
Количество информации, в сообщении, состоящем из n не равновероятных его элементов равно (эта мера предложена в 1948 г. К. Шенноном):
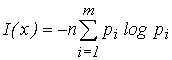. (4)
Для случая независимых равновероятных событий количество информации определяется (эта мера предложена в 1928 г. Р. Хартли):
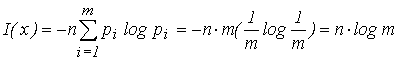(5)
Кроме этих мер информации существуют и иные, производные от энтропии статистические меры:
- расстояние Кульбака как асимметричная информационная мера:
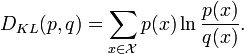
где p(x), q(x) - вероятности двух наборов случайных величин, а D - информационное расстояние от ансамбля {p} до элементов другого ансамбля {q}.
- дивергенция Кульбака как симметричная информационная мера:
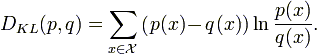
где p(x), q(x) - вероятности двух наборов случайных величин, а D - расстояние между ансамблями {p} и {q}.
1. Количество информации в сообщении обратно – пропорционально вероятности появления данного сообщения.
2. Свойство аддитивности – суммарное количество информации двух источников равно сумме информации источников.
3. Для события с одним исходом количество информации равно нулю.
4. Количество информации в дискретном сообщении растет в зависимости от увеличения объема алфавита – m.
Пример 1.
Определить количество информации в сообщении из 8 двоичных символов (n = 8, m = 2), если вероятности равны: pi0 = pi1 = 1/2.Количество информации равно:
I = n log m = 8 log2 2 = 8 бит.
Пример 2. Определить количество информации в сообщении из 8 двоичных символов (n = 8, m = 2), если вероятности равны:
pi0 = 3/4; pi1 = 1/4.
Количество информации равно:
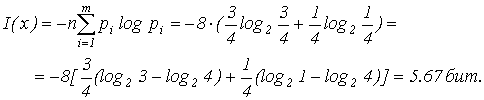
Впервые, сущность энтропии и ее меру открыл в 1871 году великий физик Людвиг Больцман. Он рассматривал количество неопределенности в ансамбле молекул газа и решил проблему физического смысла энтропии как меру хаоса в ансамбле молекул (некотором объеме газа).
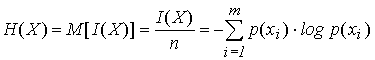. (6)
Определим максимальное значение энтропии Hmax(x). Воспользуемся методом неопределенного множителя Лагранжа -l для отыскания условного экстремума функции [6]. Находим вспомогательную функцию:
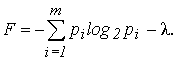(7)
Представим вспомогательную функцию
F в виде: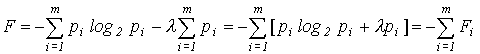
. (8)
Найдем максимум этой функции
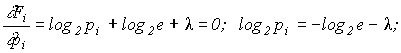т. к.
.
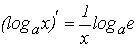Как видно из выражения, величина вероятности
pi не зависит от i, а это может быть в случае, если все pi равны, т.е. p1 =p2 =…=pm =1/m.При этом выражение для энтропии равновероятных, независимых элементов равно:
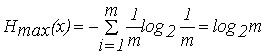. (9)
Найдем энтропию системы двух альтернативных событий с вероятностями
p1 и p2. Энтропия равна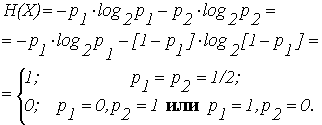
1. Энтропия есть величина вещественная, ограниченная, не отрицательная, непрерывная на интервале 0 Ј p Ј 1.
2. Энтропия максимальна для равновероятных событий.
3. Энтропия для детерминированных событий равна нулю.
4. Энтропия системы двух альтернативных событий изменяется от 0 до 1.
Энтропия численно совпадает со средним количеством информации но принципиально различны, так как:
H(x)
– выражает среднюю неопределенность состояния источника и является его объективной характеристикой, она может быть вычислена априорно, т.е. до получения сообщения при наличии статистики сообщений.I(x)
– определяется апостериорно, т.е. после получения сообщения. С получением информации о состоянии системы энтропия снижается.Одной из информационных характеристик источника дискретных сообщений является избыточность, которая определяет, какая доля максимально-возможной энтропии не используется источником
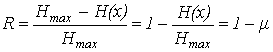, (10)
где
μ – коэффициент сжатия.Избыточность приводит к увеличению времени передачи сообщений, уменьшению скорости передачи информации, излишней загрузки канала, вместе с тем, избыточность необходима для обеспечения достоверности передаваемых данных, т.е. надежности СПД, повышения помехоустойчивости. При этом, применяя специальные коды, использующие избыточность в передаваемых сообщениях, можно обнаружить и исправить ошибки.
Пример 1. Вычислить энтропию источника, выдающего два символа 0 и 1 с вероятностями p(0) = p(1) = 1/m и определить его избыточность.
Решение: Энтропия для случая независимых, равновероятных элементов равна: H(x) = log2m = log22 = 1 [дв. ед/симв.]
При этом H(x) = Hmax(x) и избыточность равна R = 0.
Пример 2.
Вычислить энтропию источника независимых сообщений, выдающего два символа 0 и 1 с вероятностями p(0) = 3/4, p(1) = 1/4.Решение:
Энтропия для случая независимых, не равновероятных элементов равна: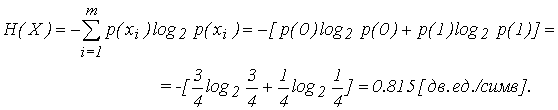
При этом избыточность равна
R = 1–0,815=0,18Пример 3.
Определить количество информации и энтропию сообщения из пяти букв, если число букв в алфавите равно 32 и все сообщения равновероятные.Решение: Общее число пятибуквенных сообщений равно: N = mn = 32
Энтропия для равновероятных сообщений равна:
H = I = – log2 1/N = log2325 = 5 log232 = 25 бит./симв.
1. Теорема Шеннона - Хартли - (на самом деле теорема Хартли, выведенная им за 15 лет до Шеннона), одна из основных теорем теории информации о передаче сигналов по каналам связи при наличии помех, приводящих к искажениям. Пусть надлежит передать последовательность символов, появляющихся с определёнными вероятностями, причём имеется некоторая вероятность того, что передаваемый символ в процессе передачи будет искажён. Простейший способ, позволяющий надёжно восстановить исходную последовательность по получаемой, состоит в том, чтобы каждый передаваемый символ повторять большое число (N) раз. Однако это приведёт к уменьшению скорости передачи в N раз, т. е. сделает её близкой к нулю. Ш. т. утверждает, что можно указать такое, зависящее только от рассматриваемых вероятностей положительное число v, что при сколько угодно малом ?>0 существуют способы передачи со скоростью v'(v' < v), сколь угодно близкой к v, дающие возможность восстанавливать исходную последовательность с вероятностью ошибки, меньшей ?. В то же время при скорости передачи v', большей v, это уже невозможно. Упомянутые способы передачи используют надлежащие «помехоустойчивые» коды. Критическая скорость v определяется из соотношения Hv = C, где Н — Энтропия источника на символ, С — ёмкость канала в двоичных единицах в секунду.
Рассматривая все возможные многоуровневые и многофазные методы шифрования, теорема Шеннона — Хартли утверждает, что пропускная способность канала C, означающая теоретическую верхнюю границу скорости передачи данных, которые можно передать с данной средней мощностью сигнала S через аналоговый канал связи, подверженный аддитивному белому гауссовскому шуму мощности N равна:
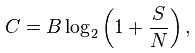
где
C — пропускная способность канала, бит/с;
B — полоса пропускания канала, Гц;
S — полная мощность сигнала над полосой пропускания, Вт или В?;
N — полная шумовая мощность над полосой пропускания, Вт или В?;
S/N — частное от деления отношения сигнала к его шуму (SNR) на гауссовский шум, выраженное как отношение мощностей.
2. Теорема Шеннона-Котельникова, теорема отсчетов - (на самом деле теорема Котельникова, доказанная им в 1933 г., когда Шеннону было еще 17 лет)
Дело в том, что в его постановке и выводах произведена подмена, аналогичная подмене в школьной шуточной задачке на сообразительность, в которой спрашивается:
- Cколько яблок на березе, если на одной ветке их 5, на другой ветке - 10 и так далее
При этом внимание учеников намеренно отвлекается от того основополагающего факта, что на березе яблоки не растут, в принципе.
В эксперименте Майкельсона ставится вопрос о движении эфира относительно покоящегося в лабораторной системе интерферометра. Однако, если мы ищем эфир, как базовую материю, из которой состоит всё вещество интерферометра, лаборатории, да и Земли в целом, то, естественно, эфир тоже будет неподвижен, так как земное вещество есть всего навсего определенным образом структурированный эфир, и никак не может двигаться относительно самого себя.
Удивительно, что этот цирковой трюк овладел на 120 лет умами физиков на полном серьезе, хотя его прототипы есть в сказках-небылицах всех народов всех времен, включая барона Мюнхаузена, вытащившего себя за волосы из болота, и призванных показать детям возможные жульничества и тем защитить их во взрослой жизни. Подробнее читайте в FAQ по эфирной физике.
|
|
 |
