Открытая система. РЕАЛЬНАЯ ФИЗИКА. Глоссарий по физике

Открытая система

Открытая система - термодинамич. система, к-рая обменивается с окружающей средой веществом, энергией и импульсом .К наиб. важному типу О. с. относятся хим. системы, в к-рых непрерывно протекают хим. реакции (извне поступают реагирующие вещества и отводятся продукты реакций). Биол. системы (живые организмы) можно также рассматривать как открытые хим. системы. Такой подход позволяет исследовать процессы их жизнедеятельности и развития на основе термодинамики неравновесных процессов, физ. и хим. кинетики.
Свойства О. с. описываются наиб. просто вблизи состояния термодинамич. равновесия. Если отклонение О. с. от термодинамич. равновесия мало, то неравновесное состояние можно охарактеризовать теми же параметрами, что и равновесное: температурой, хим. потенциалами компонентов системы и др. (но не с постоянными для всей системы значениями, а с зависящими от координат и времени). Степень неупорядоченности таких О. с., как и систем в равновесном состоянии, характеризуется энтропией. Энтропия О. с. в неравновесном (локально-неравновесном) состоянии определяется, в силу аддитивности энтропии, как сумма значений энтропии отд. малых элементов системы, находящихся в локальном равновесии (см. Локальное термодинамическое равновесие).
Отклонения термодинамич. параметров от их равновесных значений (термодинамич. силы) вызывают в системе потоки энергии вещества (см. Переноса явления ).Процессы переноса приводят к росту энтропии системы (производству энтропии).
Согласно второму началу термодинамики, в замкнутой изолиров. системе энтропия, возрастая, стремится к своему равновесному макс. значению, а произ-во энтропии - к нулю. В отличие от замкнутой системы, в О. с. возможны стационарные состоянии с пост. энтропиен при пост. произ-ве энтропии, к-рая должна при этом отводиться от системы. Стационарное состояние характеризуется постоянством скоростей хим. реакций и переноса реагирующих веществ и энергии. При таком "проточном равновесии" произ-во энтропии в О. с. минимально (Пригожина теорема ).Стационарное неравновесное состояние играет в термодинамике О. с. такую же роль, какую играет термодинамич. равновесие в термодинамике равновесных процессов. Энтропия О. с. в этом состоянии хотя и поддерживается постоянной (произ-во энтропии компенсируется её отводом), но это стационарное значение энтропии не соответствует её максимуму (в отличие от замкнутой изолпров. системы).
Наиб. интересные свойства О. с. выявляются при нелинейных процессах, когда в О. с. возможно осуществление термодинамически устойчивых неравновесных (в частном случае стационарных) состояний, далёких от состояния термодинамич. равновесия и характеризующихся определённой пространственной или временной упорядоченностью (структурой), к-рую наз. диссипативной, т. к. её существование требует непрерывного обмена веществом и энергией с окружающей средой. Нелинейные процессы в О. с. и возможность образования диссипативных структур исследуют на основе ур-ний хим. кинетики: баланса скоростей хим. реакций в системе со скоростями подачи реагирующих веществ и отвода продуктов реакций. Накопление в О. с. активных продуктов реакций или теплоты может привести к автоколебательному (самоподдерживающемуся) режиму реакций. Для этого необходимо, чтобы в системе реализовалась положительная обратная связь: ускорение реакции под воздействием либо её продукта (хим. автокатализ), либо теплоты, выделяющейся при реакции. Подобно тому как в колебат. контуре с положит. обратной связью возникают устойчивые саморегулирующиеся незатухающие колебания (автоколебания ),в хим. О. с. с положит. обратной связью возникают незатухающие саморегулирующиеся хим. реакции. Автокаталитич. реакции могут привести к неустойчивости хим. процессов в однородной среде и к появлению у О. с. стационарных состояний с упорядоченным в пространстве неоднородным распределением концентраций. В О. с. возможны также копцентрац. волны сложного нелинейного характера (автоволны ).Теория О. с. представляет особый интерес для понимания физ--хим. процессов, лежащих в основе жизни, т. к. живой организм - это устойчивая саморегулирующаяся О. с., обладающая высокой организацией как на молекулярном, так и на макроскопич. уровне. Подход к живым системам как к О. с., в к-рых протекают нелинейные хим. реакции, создаёт новые возможности для исследования процессов молекулярной самоорганизации на ранних этапах появления жизни.
Примером О. с. может служить система с четырьмя сортами молекул А, В, С, X, между к-рыми возможны две хим. реакции по схемам

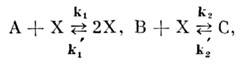
где стрелками обозначают прямую и обратную реакции, k₁, k₂, k'₁, k'₂ - константы скоростей прямой и обратной реакций. Концентрации а, b, с молекул А, В, С и константы скоростей реакций поддерживаются постоянными за счёт подвода и отвода вещества и тепла, что характерно для О. с. На практике, если кол-во веществ А, В, С велико по сравнению с кол-вом веществ X, то их концентрации можно считать постоянными.
Концентрация п веществ X может зависеть от времени t за счёт протекания хим. реакций. Из двух ур-ний баланса веществ в реакциях (с учётом действующих масс закона)следует, что

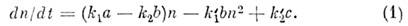
Из ур-ния (1) вытекает, что при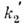 = 0 и k₁а = k₂b величина п при любом нач. условии с ростом t стремится к нулю как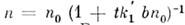 , где п₀ - нач. значение концентрации п. В этом же случае при k₁a < k₂b в пределе п также стремится к нулю, но экспоненциально, а при k₁a > k₂b величина п стремится к постоянному предельному значению, зависящему от соотношения коэф. в (1):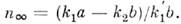 Наличие неск. предельных стационарных состояний является характерным свойством О. с., связанным с тем, что они описываются нелинейными дифференц. ур-ниями. Упрощённая модель одномодового лазера также описывается ур-нием типа (1) для числа возбуждённых атомов п при= 0 с коэф., зависящими от коэф. усиления и затухания вследствие потерь в лазере.
Учёт явлений диффузии в ур-ниях баланса хим. реакций приводит к дополнит. членам Dд²n/дx² (D - коэф. диффузии, х - пространственная координата), откуда следует, что в стационарных состояниях таких О. с. концентрации п(х)пространственно неоднородны, кроме того, при определ. условиях в них могут существовать области, где п(х)испытывает пространств. осцилляции (диссииативные структуры).
Др. примером О. с. является экологич. система "хищник - жертва", к-рая описывается ур-ниями Лотки - Вольтерры (ур-ния баланса числа "жертв" п₁ и "хищников" n₂):

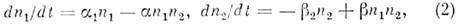
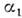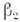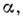
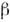где, характеризуют скорости возрастания популяций "жертв" при отсутствии "хищников" и убывания "хищников" при отсутствии "жертв". Коэф. характеризуют скорости гибели "жертв" из-за наличия "хищников" и возрастания "хищников" из-за наличия "жертв". Коэф. считаются постоянными, это означает, в частности, что запасы пищи для "жертв" достаточно велики или восполняются. Такая экологич. 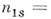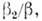система имеет два положения равновесия п_г= п₂ = 0 и 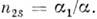Относительные числа "жертв" и "хищников" и = n₁/n_ls, v = n₂/n_2s удовлетворяют уравнению

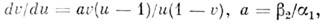
к-рое имеет решение

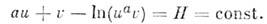
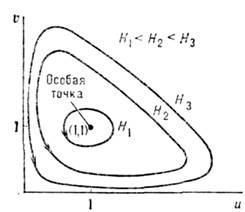
Ур-ния (2) имеют периодич. решения, к-рым соответствуют предельные циклы, изображённые на фазовой плоскости (рис.). Эти решения описывают периодич. колебания числа "жертв" и "хищников". Возможность таких незатухающих нелинейных колебаний является важным свойством О. с.
Гидродинамич. системы в турбулентном состоянии являются также примером О. с. В них возможны стационарные состояния с сильными флуктуациями из-за баланса импульса с учётом его переноса, вызванного неоднородностями флуктуации скоростей, и баланса флуктуации скоростей с учётом их релаксации и диффузии.
Открытый характер системы связан с тем, что градиент давления, обусловливающий турбулентный поток, и темп-pa поддерживаются постоянными.
Теория О. с. - одно из направлений общей теории систем, к к-рым относятся, напр., рассматриваемые в кибернетике системы переработки информации, транспортные узлы, системы энергоснабжения и др. Подобные системы, хотя и не являются термодинамическими, описываются системой ур-ний баланса, в общем случае нелинейных и сходных с аналогичными ур-ниями для физ--хим. и биол. О. с. Для всех подобных систем существуют общие проблемы регулирования и оптим. функционирования.

Литература по открытым системам

Зубарев Д. Н., Неравновесная статистическая термодинамика, М., 1971;
Гленсдорф П., Пригожин И., Термодинамическая теория структуры, устойчивости и флуктуации, пер. с англ., М., 1973;
Волькенштейн М. В., Биология и физика, "УФН", 1973, т. 109, с. 499;
Пригожин И., Николис Ж., Биологический порядок. Структура и неустойчивости, пер. с англ., там же, с. 517;
Эйген М., Самоорганизация материи и эволюция биологических макромолекул, пер. с англ., М., 1973;
Марри Д ж.. Нелинейные дифференциальные уравнения в биологии. Лекции о моделях, пер. с англ., М., 1983;
Хакен Г., Синергетика. Иерархии неустойчнвостей в самоорганизующихся системах и устройствах, пер. с англ., М., 1985.

Д. Н. Зубарев

к библиотеке к оглавлению FAQ по эфирной физике ТОЭЭ ТЭЦ ТПОИ ТИ

Знаете ли Вы, что релятивизм (СТО и ОТО) не является истинной наукой? - Истинная наука обязательно опирается на причинность и законы природы, данные нам в физических явлениях (фактах). В отличие от этого СТО и ОТО построены на аксиоматических постулатах, то есть принципиально недоказуемых догматах, в которые обязаны верить последователи этих учений. То есть релятивизм есть форма религии, культа, раздуваемого политической машиной мифического авторитета Эйнштейна и верных его последователей, возводимых в ранг святых от релятивистской физики. Подробнее читайте в FAQ по эфирной физике.

НОВОСТИ ФОРУМА

Рыцари теории эфира