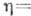
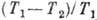 , к-рый определяется только температурой нагревателя T1 и холодильника
T2. На основании теоремы Карно удаётся построить абс. шкалу
температур (шкалу Кельвина, см. Абсолютная температура).
, к-рый определяется только температурой нагревателя T1 и холодильника
T2. На основании теоремы Карно удаётся построить абс. шкалу
температур (шкалу Кельвина, см. Абсолютная температура).Второе начало термодинамики - один из осн. законов термодинамики, устанавливающий
необратимость реальных термодинамич. процессов.
Второе начало термодинамики сформулировано как закон природы H. Л. С. Карно
(N. L. S. Carnot) в 1824, P. Клаузиусом (R. Clausius)
в 1850 и У. Томсоном (Кельвином) (W. Thomson, Kelvin) в 1851 в различных, но
эквивалентных формулировках.
Второе начало термодинамики в формулировке Клаузиуса утверждает, что
процесс, при к-ром не происходит никаких изменений, кроме передачи тепла от
горячего тела к холодному, необратим, т. е. теплота не может самопроизвольно
переходить от более холодного тела к более горячему (принцип Клаузиуса). Согласно
формулировке Томсона, процесс, при к-ром работа переходит в тепло без к--л.
иных изменений состояния системы, необратим, т. е. невозможно полностью преобразовать
в работу всё тепло,
взятое от тела, не производя никаких др. изменений состояния системы (принцип
Tомсона). Принцип Томсона эквивалентен утверждению о невозможности вечного
двигателя 2-го рода.
Второе начало термодинамики можно сформулировать также в виде принципа
Каратеодори: вблизи любого состояния термодинамич. равновесия и сколь угодно
близко к нему существует состояние, в к-рое нельзя попасть при помощи адиабатич.
процесса.
Из невозможности вечного
двигателя 2-го рода следует Карно теорема о том, что кпд любого теплового
двигателя не превосходит кпд Карно цикла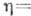
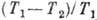 , к-рый определяется только температурой нагревателя T1 и холодильника
T2. На основании теоремы Карно удаётся построить абс. шкалу
температур (шкалу Кельвина, см. Абсолютная температура).
, к-рый определяется только температурой нагревателя T1 и холодильника
T2. На основании теоремы Карно удаётся построить абс. шкалу
температур (шкалу Кельвина, см. Абсолютная температура).
Рассматривая циклич. процесс,
при к-ром система получает (или от неё отнимают) малые кол-ва теплоты dQ при абс. температуре T, можно сформулировать
второе начало термодинамики в виде Клаузиуса
неравенства

интеграл берётся по замкнутому
циклу; если тепло отнимают, то считается, что 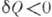 . Знак равенства относится к обратимым процессам (равенство Клаузиуса). Клаузиус
установил неравенство (1), рассматривая циклич. процесс как предел суммы большого
числа элементарных циклов Карно.
. Знак равенства относится к обратимым процессам (равенство Клаузиуса). Клаузиус
установил неравенство (1), рассматривая циклич. процесс как предел суммы большого
числа элементарных циклов Карно.
Из равенства Клаузиуса
следует, что для равновесного процесса 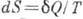 есть полный дифференциал функции состояния S, наз. энтропией. Если
учесть первое начало термодинамики ,согласно к-рому
есть полный дифференциал функции состояния S, наз. энтропией. Если
учесть первое начало термодинамики ,согласно к-рому

(U - внутр. энергия,
P - давление, V - объём), то из
второго начала термодинамики следует, что существует
интегрирующий множитель T-1, к-рый делает выражение (2) полным
дифференциалом 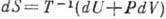 . Поэтому второе начало термодинамики можно сформулировать в виде неравенства
. Поэтому второе начало термодинамики можно сформулировать в виде неравенства 
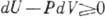 .
Неравенство Клаузиуса можно записать в
след. виде:
.
Неравенство Клаузиуса можно записать в
след. виде:  (знак равенства соответствует обратимым процессам). Это неравенство - другая,
интегральная формулировка второго начала термодинамики. Из него следует, что для адиабатически изолиров.
системы
(знак равенства соответствует обратимым процессам). Это неравенство - другая,
интегральная формулировка второго начала термодинамики. Из него следует, что для адиабатически изолиров.
системы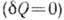 при необратимых процессах энтропия возрастает, а при обратимых - остаётся неизменной.
при необратимых процессах энтропия возрастает, а при обратимых - остаётся неизменной.
Др. эквивалентные формулировки второго начала термодинамики можно получить с помощью любого термодинамического потенциала. Напр.,
для Гельмгольца энергии (свободной энергии) 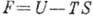 получим
получим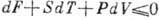 .
.
При выборе в качестве термодинамич.
потенциала Гиббса энергии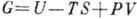 получим
получим 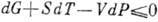
В кинетической теории газов второе начало термодинамики является следствием
Болъцмана Н-теоремы, т. к. Н-функция
Больцмана, определяемая через ср. логарифм функции распределения атомов, пропорциональна
энтропии идеального газа. Поэтому убывание энтропии имеет не абсолютный, а вероятностный
характер.
В статистич. физике выясняется физ. смысл энтропии, связанной с логарифмом термодинамической вероятности W соотношением Больцмана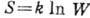 . Термодинамич. вероятность
. Термодинамич. вероятность 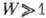 определяется статистич. весом макроскопич. состояния. Возрастание энтропии означает
переход системы из менее вероятного состояния в более вероятное.
определяется статистич. весом макроскопич. состояния. Возрастание энтропии означает
переход системы из менее вероятного состояния в более вероятное.
В термодинамике неравновесных
процессов второго начала термодинамики оказывается следствием положительности производства энтропии
(т. е. скорости её возрастания), к-рое является положительно определённой квадратичной
формой от термодинамич. сил, характеризующих отклонение системы от состояния
термодинамич. равновесия. T. о., неравновесная термодинамика даёт количественную
характеристику второго начала термодинамики.
В статистич. физике устанавливают пределы применимости второго начала термодинамики, связанные с существованием флуктуации энтропии. Вывод о "тепловой смерти" Вселенной, к-рый иногда делают на основе применения к ней второго начала термодинамики как к замкнутой термодинамич. системе, не является правомерным. Ошибочны также попытки опровергнуть этот вывод, учитывая возможность флуктуации, как это было сделано Л. Больцманом (L. Boltzmann). Дело в том, что в эволюции Вселенной существенную роль играет тяготение, которое не принималось во внимание.

|
|