 и спиновую плотность волны можно рассматривать как одно из проявлений антиферромагнетизма .Пространственное распределение М(r)описывается соотношением:
и спиновую плотность волны можно рассматривать как одно из проявлений антиферромагнетизма .Пространственное распределение М(r)описывается соотношением:
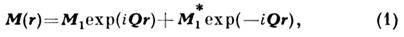
Спиновая плотность волны - термодинамически равновесное
состояние вещества, характеризующееся пространственно неоднородным периодич.
распределением плотности магн. момента М(r). При этом усреднённый
макроскопич. магн. момент системы равен нулю и спиновую плотность волны можно рассматривать как одно из проявлений антиферромагнетизма .Пространственное распределение М(r)описывается соотношением:
и спиновую плотность волны можно рассматривать как одно из проявлений антиферромагнетизма .Пространственное распределение М(r)описывается соотношением:
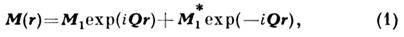
где Q - волновой вектор спиновой плотности волны.
Чаще всего под спиновой плотностью волны понимают антиферромагнетизм системы взаимодействующих коллективизиров. электронов (см. Зонный магнетизм ).Парамагн. осн. состояние однородного электронного газа может оказаться неустойчивым относительно образования спиновой плотности волны. Неустойчивость зависит от характера взаимодействия между электронами. Особенности зонной структуры могут стабилизировать спиновую плотность волны, т. е. привести к антиферромагн. осн. состоянию электронной системы.
Критерий неустойчивости парамагн. состояния зонного магнетика (см. Стонера
критерий ферромагнетизма)определяется не только величиной потенциала
межэлектронного взаимодействия, но и зависимостью магн. восприимчивости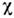 от
электронного волнового вектора q. Напр., если в силу к--л. особенности
топологии фермаповерхности
от
электронного волнового вектора q. Напр., если в силу к--л. особенности
топологии фермаповерхности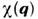 обладает резко выраженным максимумом при нек-ром значении
обладает резко выраженным максимумом при нек-ром значении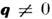 ,
то фазовый переход при
,
то фазовый переход при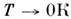 из парамагн. состояния в состояние с спиновой плотностью волны может иметь место даже при
слабом взаимодействии между электронами. Наличие конгруэнтных (совпадающих
при трансляции на волновой вектор Q)электронных и дырочных участков
на поверхности Ферми (н е с т и н г) в веществах с металлич. проводимостью
приводит к возможности триплетного электрон-дырочного спаривания с
возникновением спиновой плотности волны.
из парамагн. состояния в состояние с спиновой плотностью волны может иметь место даже при
слабом взаимодействии между электронами. Наличие конгруэнтных (совпадающих
при трансляции на волновой вектор Q)электронных и дырочных участков
на поверхности Ферми (н е с т и н г) в веществах с металлич. проводимостью
приводит к возможности триплетного электрон-дырочного спаривания с
возникновением спиновой плотности волны.
наиб. подходящей моделью для микроскопич. описания фазового перехода
в состояние с спиновой плотностью волны является модель экситонного диэлектрика. В
системах с спиновой плотностью волны появляются щель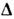 в электронном энергетич. спектре и особенности плотности состояний на
краях этой щели. С этим связаны особенности оптич., кинетич., магн., упругих
и др. свойств спиновой плотности волны. От краёв щели «отщепляются» спин-поляризов. состояния,
отсутствующие в парамагн. фазе и приводящие к резонансным аномалиям кинетич.
свойств. Необычно и поведение дефектов: в окрестности дефекта происходит
дополнит. перераспределение спиновой плотности, т. в. формируется ближний
антиферромагн. порядок, сохраняющий-
в электронном энергетич. спектре и особенности плотности состояний на
краях этой щели. С этим связаны особенности оптич., кинетич., магн., упругих
и др. свойств спиновой плотности волны. От краёв щели «отщепляются» спин-поляризов. состояния,
отсутствующие в парамагн. фазе и приводящие к резонансным аномалиям кинетич.
свойств. Необычно и поведение дефектов: в окрестности дефекта происходит
дополнит. перераспределение спиновой плотности, т. в. формируется ближний
антиферромагн. порядок, сохраняющий-
ся иногда выше точки Нееля TN (локализованная
спиновая плотность волны). На фоне осн. состояния ниже точки Нееля Т < ТN в электронном газе формируются своеобразные коллективные возбуждения
спиновой плотности (амплитудоны, фазоны, спиновая плотность волны - магноны).
Теория предсказывает также существование слабо затухающих коллективных
возбуждений выше ТN. С. п. в. образуется в результате
фазового перехода (обычно 2-го рода, хотя возможны фазовые превращения
1-го рода) при температуре ниже точки Нееля (рис.).
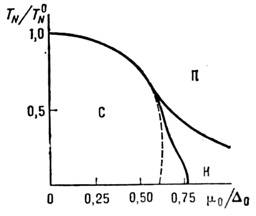
Фазовая диаграмма экситонного диэлектрика для фазового перехода в
состояние волны спиновой плотности (2-го рода): П - парамагнитная фаза;
С - антиферромагнитная соизмеримая фаза; Н - антиферромагнитная несоизмеримая
фаза;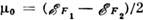 ,
,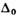 соответствует
Т = 0 К,
соответствует
Т = 0 К,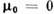 , ТN - темп-pa перехода в состояние волны спиновой плотности
при
, ТN - темп-pa перехода в состояние волны спиновой плотности
при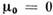
Пространственный период волны может выражаться через целое число постоянных кристаллич. решётки (соизмеримая фаза), но возможно появление и несоизмеримых сверхструктур, т. е. спиновая плотность волны, период к-рых не кратен периоду кристаллич. решётки.
В переходных металлах и их сплавах реализуется ситуация, когда Q
= G/2, где G - вектор обратной решётки, что соответствует соизмеримой фазе. В более общем случае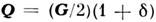 , где
, где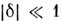 и зависит от Т, что соответствует несоизмеримой фазе.
и зависит от Т, что соответствует несоизмеримой фазе.
Среди чистых металлов, в к-рых наблюдаются спиновые плотности волн, наиб. исследован
Сr, поверхность Ферми к-рого обладает двумя конгруэнтными участками: дырочным
октаэдром, центрированным в точке Н Бриллюэна зоны, и электронным
квазиоктаэдром, центрированным в точке Г. Октаэдрич. грани перпендикулярны
к направлению [111], и электронный октаэдр меньше дырочного. Значит. часть
этих двух листов поверхности Ферми может быть совмещена трансляцией на
волновой вектор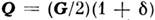 , где
, где при Т = 0 K. При этом суммарные объёмы электронного и дырочного
октаэдров примерно равны, и в фазе спиновой плотности волны эти октаэдры исчезают, перекрытые
щелью.
при Т = 0 K. При этом суммарные объёмы электронного и дырочного
октаэдров примерно равны, и в фазе спиновой плотности волны эти октаэдры исчезают, перекрытые
щелью.
Измерения нейтронной дифракции на монокристаллах Сr показали, что магн.
упорядочение в нём существенно отличается от обычного антиферромагнетизма
(см. Магнитная нейтронография ),причём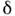 имеет слабую температурную зависимость (при Т ~ TN величина
имеет слабую температурную зависимость (при Т ~ TN величина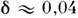 ). Выше TN ср. магн. момент на 1 атом Сr порядка
). Выше TN ср. магн. момент на 1 атом Сr порядка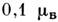 (в ферромагн. фазе он составляет
(в ферромагн. фазе он составляет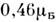 ). Темп-pa Нееля чистого
). Темп-pa Нееля чистого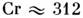 К; при Т < 120 К поперечная модуляция периодической магн. структуры
сменяется на продольную - происходит т. н. с п и н - ф л и п переход.
К; при Т < 120 К поперечная модуляция периодической магн. структуры
сменяется на продольную - происходит т. н. с п и н - ф л и п переход.
Теория зонного
антиферромагнетизма и спиновой плотности волны позволила интерпретировать
магн. свойства сплавов Сг. Концентрац. фазовые диаграммы этих сплавов,
переход из несоизмеримой структуры в соизмеримую, изменение магн. структуры
и свойств под давлением и др. особенности также хорошо описываются моделью
экситонного диэлектрика. При этом в сплавах Сг с немагнитными переходными
металлами изменение состава сплава влияет на TN и параметры
структуры спиновой плотности волны. Напр., для сплавов с Мо и W влияние примесного рассеяния
электронов - единств, причина изменения TN и параметров
структуры. Для сплавов с металламидонорами (Mn, Re, Os, Rh и др.) с ростом
их концентрации происходит выравнивание объёмов электронного и дырочного
октаэдров, и при нек-рой концентрации примеси происходит переход из модулированной
в чисто удвоенную антиферромагн. структуру. Для металлов-акцепторов (V,
Ni) с ростом их концентрации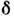 растёт. Зависимость TN от концентрации примеси для доноров
немонотонная, для акцепторов - падающая.
растёт. Зависимость TN от концентрации примеси для доноров
немонотонная, для акцепторов - падающая.
Выявлены и др. металлич. системы, в к-рых имеет место переход из парамагн.
состояния в состояние со спиновой плотностью волны. К ним относятся редкоземельные металлы
и их сплавы с переходными металлами, обладающие геликоидальной антиферромагн.
структурой. В этих веществах поверхность Ферми имеет конгруэнтные «ленточные»
участки . Примерами таких систем служат Еu и сплавы Y и Se с тяжёлыми редкоземельными
металлами (Tb, Gd, Dy, Но). В сплавах Y и Sc с Ег и Тm реализуется синусоидальная
антиферромагн. структура, т. е. спиновая плотность волны, происхождение к-рой также связано
с особенностью поверхности Ферми.
. Примерами таких систем служат Еu и сплавы Y и Se с тяжёлыми редкоземельными
металлами (Tb, Gd, Dy, Но). В сплавах Y и Sc с Ег и Тm реализуется синусоидальная
антиферромагн. структура, т. е. спиновая плотность волны, происхождение к-рой также связано
с особенностью поверхности Ферми.
Сплавы и соединения переходных металлов также испытывают переход из
парамагн. состояния в состояние спиновой плотности волны. К таким системам относятся упорядоченные
сплавы FeRh, Pt3Fe, MnNi, геликоидальные магнетики FeGe2,
MnS2, соединение СrВ2, сложные халькогени-ды ванадия
(V3S4, V5S8), возможно, сульфид
никеля NiS и интерметаллические соединения ИЗ группы фаз Лавеса
TiBe2 и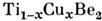 . В т. н. ф а з а х Магнелли
. В т. н. ф а з а х Магнелли при
при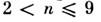 также
имеет место переход в фазу спиновой плотности волны, причём на фоне волны зарядовой
плотности. В ряде актинидных соединений с тяжёлыми фермионами (URuSi2,
UCu5, UCd11, U2Zn7, U1-xThxPt3)
Спиновая плотность волны формируется при низких температурах в фазе тяжёлой ферми-жидкости.
Конкретное применение модели спиновой плотности волны к перечисленным объектам требует
учёта дополнит. эффектов - магнитострикции, спиновой поляризации
остальных участков поверхности Ферми, наличия вблизи неё т. н. резонанса
Абрикосова - Суда (см. Промежуточная валентность).
также
имеет место переход в фазу спиновой плотности волны, причём на фоне волны зарядовой
плотности. В ряде актинидных соединений с тяжёлыми фермионами (URuSi2,
UCu5, UCd11, U2Zn7, U1-xThxPt3)
Спиновая плотность волны формируется при низких температурах в фазе тяжёлой ферми-жидкости.
Конкретное применение модели спиновой плотности волны к перечисленным объектам требует
учёта дополнит. эффектов - магнитострикции, спиновой поляризации
остальных участков поверхности Ферми, наличия вблизи неё т. н. резонанса
Абрикосова - Суда (см. Промежуточная валентность).
Особой группой веществ, в к-рых наблюдались состояния спиновой плотности волны, являются нек-рые квазиодномерные органические проводники ,напр. (TMTSF)2X - тетраметил-тетраселенфульвален, где X - анионы (X = PF6, AsF6). Установлено также существование спиновой плотности волны и с нек-рыми др. анионами. Переходу в антиферромагн. фазу отвечает спиновая плотность волны с удвоенным (по сравнению с постоянной решётки) периодом в продольном направлении. Возможно, что магн. упорядочение в металлооксидах типа La-Sr-Сu-О и Y-Ва-Сu-О также представляет собой спиновую плотность волны, что связано с проблемой высокотемпературной сверхпроводимости (см. Оксидные высокотемпературные сверхпроводники).
В широком смысле понятие спиновой плотностью волны может быть обобщено на случай произвольных периодич. сверхструктур в антиферромагнетиках (геликоидальные, синусоидальные структуры). Феноменелогич. теория магн. сверхструктур основывается на теории фазовых переходов 2-го рода. В неметаллах формирование сверхструктур происходит под влиянием релятивистских взаимодействий спин - решётка и спин - спин, а также вследствие анизотропного обменного взаимодействия. Периоды сверхструктур в антиферромагн. металлах определяются взаимодействием электронов проводимости со спинами магн. ионов и мало отличаются от величин, обратных экстремальным диаметрам поверхности Ферми.

В. В. Тугушев, Е. П. Башкин
Релятивисты и позитивисты утверждают, что "мысленный эксперимент" весьма полезный интрумент для проверки теорий (также возникающих в нашем уме) на непротиворечивость. В этом они обманывают людей, так как любая проверка может осуществляться только независимым от объекта проверки источником. Сам заявитель гипотезы не может быть проверкой своего же заявления, так как причина самого этого заявления есть отсутствие видимых для заявителя противоречий в заявлении.
Это мы видим на примере СТО и ОТО, превратившихся в своеобразный вид религии, управляющей наукой и общественным мнением. Никакое количество фактов, противоречащих им, не может преодолеть формулу Эйнштейна: "Если факт не соответствует теории - измените факт" (В другом варианте " - Факт не соответствует теории? - Тем хуже для факта").
Максимально, на что может претендовать "мысленный эксперимент" - это только на внутреннюю непротиворечивость гипотезы в рамках собственной, часто отнюдь не истинной логики заявителя. Соответсвие практике это не проверяет. Настоящая проверка может состояться только в действительном физическом эксперименте.
Эксперимент на то и эксперимент, что он есть не изощрение мысли, а проверка мысли. Непротиворечивая внутри себя мысль не может сама себя проверить. Это доказано Куртом Гёделем.
Понятие "мысленный эксперимент" придумано специально спекулянтами - релятивистами для шулерской подмены реальной проверки мысли на практике (эксперимента) своим "честным словом". Подробнее читайте в FAQ по эфирной физике.
|
|