к библиотеке к оглавлению FAQ по эфирной физике ТОЭЭ ТЭЦ ТПОИ ТИ

РЕАЛЬНАЯ ФИЗИКА

Глоссарий по физике

А Б В Г Д Е Ж З И К Л М Н О П Р С Т У Ф Х Ц Ч Ш Э Ю Я

Обратная решётка

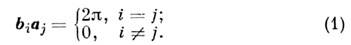
Обратная решётка - периодпч. решётка в обратном пространстве, элементарные векторы трансляции к-рой b_i связаны с осн. векторами трансляции a_iисходной Браве решётки (прямой решётки) условиями

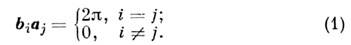
Узлы О. р. задаются соотношениями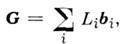где L_i - произвольные целые числа, i = 1, 2, 3 для трёхмерной решётки, i= 1, 2 для двухмерной. Размерность О. р. совпадает с размерностью прямой решётки. Так, для трёхмерной прямой решётки О. р. является трёхмерной с элементарными векторами трансляции, равными в соответствии с (1):

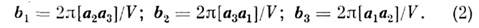
Здесь V = (а₁[а₂а₃]) - объём элементарной ячейки прямой решётки; объём элементарной ячейки О. р. равен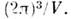 Вектор О. p. G_hkl = hb₁ + kb₂ + lb₃перпендикулярен плоскости с индексами кристаллографическими h, k, l.
Между прямыми и О. р. имеется взаимно однозначное соответствие, причём прямая решётка является обратной к обратной. Поэтому для каждого кристалла О. р. вводится однозначно, а симметрия О. р. полностью определяется симметрией решётки Браве кристалла. Напр.. О. р. для простой кубич. решётки - простая кубическая, для гранецентрир. кубической - объёмно-центрир. кубическая (и наоборот) и т. д.
Понятие О. р. является одним из основных в физике твёрдого тела. О. р. определяет структуру пространства квазиимпульсов квазичастиц. Их волновые векторы определены с точностью до векторов трансляции О. p. G; состояния квазичастиц, для которых квазиимпульсы отличаются на величину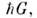 а остальные квантовые числа одинаковы, тождественны. Поэтому область всех физически неэквивалентных значений волнового вектора квазичастицы образует элементарную ячейку О. р. Соответственно энергетич. спектр квазичастиц и др. функции волнового вектора являются периодич. функциями векторов трансляции О. р. При этом мн. характеристики квазичастиц кристалла могут задаваться разложением в ряд Фурье по векторам трансляции О. р. Это позволяет перейти к квазиимпульсному представлению для операторов и волновых функций квазичастиц по аналогии с переходом к импульсному представлению для частиц в свободном пространстве (см. Импульсное представление в квантовой механике).
Экстремумы энергетич. спектра обычно соответствуют точкам высокой симметрии ячеек О. р. При столкновениях квазичастиц сумма их квазиимпульсов сохраняется с точностью до G (см. Переброса процессы). Вигнера - Зейтца ячейка О. р. является первой Бриллюэна зоной для кристалла.
О. р. - важный матем. образ, находящий многочисл. применения в кристаллографии и физике твёрдого тела. Напр., понятие О. р. удобно использовать при описании дифракции частиц на кристаллич. решётке (см. Дифракция нейтронов, Нейтронография структурная, Рентгеновский структурный анализ, Электронография). Соответственно нейтроно- и рентгенограммы кристалла могут дать "изображение" О. р.

Литература по обратным решёткам

Современная кристаллография, т. 1, М., 1979.

А. Э. Мейерович

к библиотеке к оглавлению FAQ по эфирной физике ТОЭЭ ТЭЦ ТПОИ ТИ

Знаете ли Вы, что релятивистское объяснение феномену CMB (космическому микроволновому излучению) придумал человек выдающейся фантазии Иосиф Шкловский (помните книжку миллионного тиража "Вселенная, жизнь, разум"?). Он выдвинул совершенно абсурдную идею, заключавшуюся в том, что это есть "реликтовое" излучение, оставшееся после "Большого Взрыва", то есть от момента "рождения" Вселенной. Хотя из простой логики следует, что Вселенная есть всё, а значит, у нее нет ни начала, ни конца... Подробнее читайте в FAQ по эфирной физике.

НОВОСТИ ФОРУМА

Рыцари теории эфира