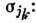
Пьезомагнетизм (пьезомагнитный эффект) - возникновение в веществе спонтанного магнитного момента при наложении
упругих напряжений. П. может сушествовать только в антиферромагнетиках и ферромагнетиках
и принципиально невозможен в пара-и диамагнетиках.
Термодинамич. рассмотрение вопроса о П. основывается
на выделении и изучении в разложении термодинамического потенциала F
членов, линейных по магн. полю Hi и по одной
из компонент тензора упругих напряжений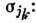
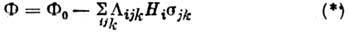
Если все преобразования магн. симметрии данного
кристалла оставляют инвариантным хотя бы один член в этом выражении, то соответствующий
коэф.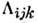 (модуль
П.) будет отличен от нуля и в кристалле будет возникать пьезомагн. момент
(модуль
П.) будет отличен от нуля и в кристалле будет возникать пьезомагн. момент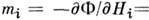 =
=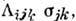 зависящий
от приложенного напряжения
зависящий
от приложенного напряжения 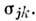 Эта идея впервые была высказана В. Фойгтом [1]. Однако он ошибочно считал, что
достаточно учитывать только кристаллографич. симметрию.
Эта идея впервые была высказана В. Фойгтом [1]. Однако он ошибочно считал, что
достаточно учитывать только кристаллографич. симметрию.
Пара- или диамагнитный кристалл не может быть
пьезомагнетиком, поскольку в группу магн. симметрии такого кристалла самостоятельно
входит элемент инверсии времени Л, к-рый изменяет знаки магн. полей и моментов
на обратные (см. Магнитная симметрия ).Поэтому для пара- и диамагнетиков
все компоненты пьезомагн. тензора 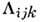 тождественно
равны нулю. В веществах, обладающих упорядоченной магн. структурой (в ферромагнетиках
и антиферромагнетиках), R встречается только в комбинациях с др. элементами
симметрии. Поэтому в принципе такие вещества могут быть пьезомагнетиками [2].
Симметрийный анализ позволил установить все классы магн. симметрии, к-рые допускают
П. Их оказалось 66, и для всех найден вид тензоров
тождественно
равны нулю. В веществах, обладающих упорядоченной магн. структурой (в ферромагнетиках
и антиферромагнетиках), R встречается только в комбинациях с др. элементами
симметрии. Поэтому в принципе такие вещества могут быть пьезомагнетиками [2].
Симметрийный анализ позволил установить все классы магн. симметрии, к-рые допускают
П. Их оказалось 66, и для всех найден вид тензоров 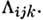 Благодаря симметрии тензора sjk пьезомагн. тензоры могут
быть представлены в виде матриц 3 x 6, и число таких матриц равно 16 [3].
Благодаря симметрии тензора sjk пьезомагн. тензоры могут
быть представлены в виде матриц 3 x 6, и число таких матриц равно 16 [3].
Пьезомагн. момент сравнительно мал. Поэтому практически
наблюдать его можно только в антиферромагнетиках, к-рые в нормальных условиях
не обладают спонтанным магн. моментом. Теоретич. исследование магн. симметрии
известных антиферромагнетиков позволило И. Е. Дзяяошинскому [4] (ещё до того,
как были найдены все магн. классы, допускающие П.) найти среди них ряд веществ
(Fe203, FeCO2, MnF2, CoF2,
FeF2), в к-рых должен наблюдаться П.
П. в антиферромагнетиках тесно связан с явлением
слабого ферромагнетизма. Так же, как и магн. момент слабых ферромагнетиков,
пьезомагн. момент может быть направлен перпендикулярно к направлению спонтанной
намагниченности магнитных подрешёток или параллельно ему. В первом случае
возникает скос векторов подрешёток, приводящий к возникновению пьезомагн. момента.
Продольный П. связан с изменением намагниченности подрешёток.
Экспериментально П. обнаружен в 1959 в антифер-ромагн.
кристаллах MnF2 и CoF2 [5]. В этих кристаллах в соответствии
с соображениями симметрии отличны от нуля только три компоненты пьезомагн. тензора:
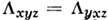 и
и 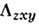 .
Для CoF2 пьезомагн. модули при температуре
20.4 R имеют следующие значения: Lxyz = 2·10-3
Гс·см2/кГ и Lzxy=0,8·10-3 Гс·см2/кГ.
На примере антиферромагн. фторидов легко понять микроскопич. природу продольного
пьезомагн. эффекта.
.
Для CoF2 пьезомагн. модули при температуре
20.4 R имеют следующие значения: Lxyz = 2·10-3
Гс·см2/кГ и Lzxy=0,8·10-3 Гс·см2/кГ.
На примере антиферромагн. фторидов легко понять микроскопич. природу продольного
пьезомагн. эффекта.
Рис. 1. Схематическое изображение деформированной
элементарной ячейки (d - период ячейки) антиферромагнитных фторидов переходных
металлов (CoF2). Ось г перпендикулярна плоскости чертежа.
Ионы, обозначенные заштрихованными кружками, сдвинуты на половину периода кристаллической
решётки вдоль оси z относительно незаштрихованных.
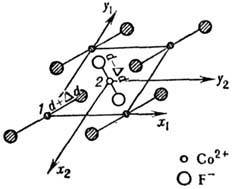
На рис. 1 показана схема расположения попив в
деформированной тетрагональной решётке, когда кристаллографически эквивалентные
узлы 1 и 2 после сдвиговой деформации в плоскости ху перестают
быть эквивалентными. При этом расстояние d до ближайших ионов фтора для
магн. ионов в подрешётке 1 увеличивается, а для ионов в подрешётке 2 - уменьшается.
Очевидно, что при этом изменения величины
намагниченности подрешёток должны быть противоположными и их равенство будет
нарушаться [6]. Из рис. 2 видно, что температурная
зависимость пьезомагн. модуля аналогична температурной зависимости намагниченности
подрешёток.
Рис. 2. Температурная зависимость модуля пьезомагнетизма
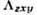 у CoF2
(точки - данные эксперимента).
у CoF2
(точки - данные эксперимента).
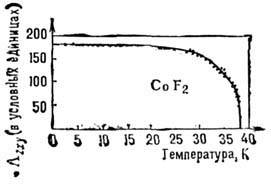
П. существенно зависит от доменной структуры
антиферромагнетика. 180-градусные домены отличаются знаком антиферромагн. вектора
 и
и 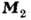 - намагниченности подрешёток), а компоненты тензора П. линейно зависят от компонент
вектора
- намагниченности подрешёток), а компоненты тензора П. линейно зависят от компонент
вектора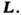 В многодоменном
антиферромагн. образце П. может быть сильно ослаблен. Поэтому П. в чистом виде
наблюдают в однодоменных образцах. При перемагничива-нии однодоменного образца,
обладающего пьезомагн. моментом, происходит переворот домена и соответственно
векторы намагниченности подрешёток поворачиваются на 180°. Используя П.,
легко получать одно-доменные антиферромагн. кристаллы, охлаждая их из парамагн.
состояния в магн. поле при соответствующей деформации. Это было подтверждено
методами нейтронографии.
В многодоменном
антиферромагн. образце П. может быть сильно ослаблен. Поэтому П. в чистом виде
наблюдают в однодоменных образцах. При перемагничива-нии однодоменного образца,
обладающего пьезомагн. моментом, происходит переворот домена и соответственно
векторы намагниченности подрешёток поворачиваются на 180°. Используя П.,
легко получать одно-доменные антиферромагн. кристаллы, охлаждая их из парамагн.
состояния в магн. поле при соответствующей деформации. Это было подтверждено
методами нейтронографии.
П. наблюдался также в FeCO3 и в низкотемпературной
модификации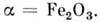 Магн. симметрия обоих веществ одинакова, и в них наблюдаются следующие отличные
от нуля компоненты тензора П.:
Магн. симметрия обоих веществ одинакова, и в них наблюдаются следующие отличные
от нуля компоненты тензора П.: 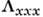 =
=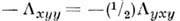 и
и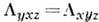 .
Их величина примерно на порядок меньше, чем у CoF2. В высокотемпературной
модификации a = Fe2O3 удалось измерить только один
модуль П.-
.
Их величина примерно на порядок меньше, чем у CoF2. В высокотемпературной
модификации a = Fe2O3 удалось измерить только один
модуль П.-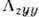 ,
величина к-рого тоже на порядок меньше, чем у CoF2.
,
величина к-рого тоже на порядок меньше, чем у CoF2.
Из ф-лы (*) видно, что наряду с П. должен существовать
обратный эффект - линейная магнитострикция ,при к-рой компоненты тензора
деформаций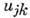 линейно связаны с магн. полем:
линейно связаны с магн. полем:  =
=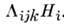 ,
Знак линейной магнитострикции, как и
,
Знак линейной магнитострикции, как и 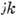 в случае П., зависит от знака вектора
в случае П., зависит от знака вектора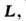 характеризующего
образовавшееся доменное состояние образца. Линейная магнитострикция наблюдалась
в CoF2 и a = Fe203 (в обеих антиферромагн.
модификациях). В ходе исследования линейной магнитострикции в этих веществах
было обнаружено, что в сильных магн. полях знак магнитострикции может скачком
изменяться, что указывает на индуцированное полем скачкообразное изменение доменной
структуры антиферромагнетика (поворот вектора антиферромагнетизма
характеризующего
образовавшееся доменное состояние образца. Линейная магнитострикция наблюдалась
в CoF2 и a = Fe203 (в обеих антиферромагн.
модификациях). В ходе исследования линейной магнитострикции в этих веществах
было обнаружено, что в сильных магн. полях знак магнитострикции может скачком
изменяться, что указывает на индуцированное полем скачкообразное изменение доменной
структуры антиферромагнетика (поворот вектора антиферромагнетизма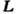 на
180°). Линейная магнитострикция наблюдалась также при спин-переориентац.
переходах в ортоферритах (YFe03 и DyFeO3) и ортохромитах
(YCrO3) (см. Магнитный фазовый переход ).В этих соединениях
в определ. интервале значений температуры направление антиферромагн. вектора
на
180°). Линейная магнитострикция наблюдалась также при спин-переориентац.
переходах в ортоферритах (YFe03 и DyFeO3) и ортохромитах
(YCrO3) (см. Магнитный фазовый переход ).В этих соединениях
в определ. интервале значений температуры направление антиферромагн. вектора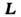 плавно
изменяется от одного кристал-лографич. направления к другому. При этом, как
показывает симметрийный анализ, должна наблюдаться линейная магнитострикция,
приводящая к моноклинному искажению орторомбич. решётки. Направление вектора
L антиферромагн. домена и в этом случае определяет знак магнитострикции. Линейная
магнитострикция даёт значит. вклад в магнитоупругие свойства антиферромагнетиков
вблизи Нееля точки
плавно
изменяется от одного кристал-лографич. направления к другому. При этом, как
показывает симметрийный анализ, должна наблюдаться линейная магнитострикция,
приводящая к моноклинному искажению орторомбич. решётки. Направление вектора
L антиферромагн. домена и в этом случае определяет знак магнитострикции. Линейная
магнитострикция даёт значит. вклад в магнитоупругие свойства антиферромагнетиков
вблизи Нееля точки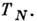
Симметрийным аналогом линейной магнитострикции является эффект линейного по магн. полю магн. двулу-чепреломления. В отличие от обычного квадратичного по полю Коттона-Мутона эффекта, линейное дву-лучепреломление наблюдается в одноосных антиферромагнетиках при приложении магн. поля вдоль оси антиферромагнетизма [7].

А. С. Боровик-Романов
Вещество и поле не есть что-то отдельное от эфира, также как и человеческое тело не есть что-то отдельное от атомов и молекул его составляющих. Оно и есть эти атомы и молекулы, собранные в определенном порядке. Также и вещество не есть что-то отдельное от элементарных частиц, а оно состоит из них как базовой материи. Также и элементарные частицы состоят из частиц эфира как базовой материи нижнего уровня. Таким образом, всё, что есть во вселенной - это есть эфир. Эфира 100%. Из него состоят элементарные частицы, а из них всё остальное. Подробнее читайте в FAQ по эфирной физике.
|
|