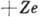Глоссарий по физике

Атом

АТОМ - наименьшая часть хим. элемента, способная к самостоят. существованию и являющаяся носителем его свойств. Каждому элементу соответствует определ. род А., обозначаемый хим. символом этого элемента. А. могут существовать в свободном состоянии в газах. В связанном состоянии А. входят в состав молекул, соединяясь химически с атомами того же элемента или др. элементов, и конденсир. тел (см. Жидкость, Твёрдое тело). В статье будут рассматриваться свободные А. Физ. и хим. свойства свободного А. определяются его составом и строением.

Общая характеристика строения атома. А. состоит из электрически положительно заряженного ядра и отрицательно заряженных электронов. Принадлежность А. данному элементу определяется величиной заряда ядра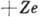 (е - величина элементарного электрич. заряда, Z - ат. номер).

Число электронов в нейтральном А. равно Z, их общий отрицат. заряд равен -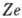. Теряя электроны, нейтральный А. превращается в ионизир. А.- положительно заряженный ион, а после присоединения одного или неск. электронов - в отрицат. ион. Число электронов, к-рое А. потерял (присоединил), определяет кратность иона. Нейтральный А. обозначают символом элемента, для ионов к символу А. добавляют индексы справа сверху, напр. 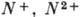(или 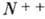), 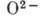- однократно и двукратно ионизированные А. азота (положит. ионы), двукратный отрицат. ион кислорода.

Нейтральный А. элемента и ионы А. др. элементов с тем же числом электронов образуют изоэлектронный ряд (напр., Водородоподобные атомы). Членам изоэлектронного ряда присуще значит. сходство в строении А., многие их свойства закономерно изменяются с изменением Z.

Размеры А. определяются размерами его электронной оболочки, не имеющей строго определ. границ, поэтому значения радиуса и объёма А. зависят от способа их эксперим. определения. Размеры А. могут быть получены из определения постоянной b в Ван-дер-Ваалъса уравнении, средней длины свободного пробега в газе, из расстояния между А. в кристаллич. решётке и др. способами. Линейные размеры А.~ 10^-8 см, площадь поперечных сечений ~10^-16см², объём ~10^-24 см³.

В теории атома Бора (см. Атомная физика)радиус простейшего А.- А. водорода - имеет точно определ. значение и равняется радиусу наименьшей возможной круговой орбиты: а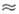0,53*10^-8 см (точнее, 0,52917*10^-8 см). Эта величина оказывается удобной естеств. единицей для измерения линейных размеров (см. Естественные системы единиц).

Линейные размеры атомных ядер много меньше линейных размеров A. (~10^-13-10^-12 см), поэтому ядро часто рассматривают как точечный заряд и лишь для тонких эффектов взаимодействия ядра с электронными оболочками учитывают его конечные размеры.

Масса А. определяется в осн. массой его ядра и возрастает пропорционально массовому числу А, т. е. общему числу протонов и нейтронов - числу нуклонов в ядре (ядро содержит Z протонов к А - Z нейтронов). Масса электрона (0,91*10^-27 г) примерно в 1840 раз меньше массы протона или нейтрона (1,67*10^-24 г), поэтому центр тяжести А. практически совпадает с ядром и можно приближённо считать, что в системе координат, связанной с А., движутся только электроны, а ядро покоится. Учёт движения ядра относительно общего центра тяжести ядра и электронов приводит в теории А. лишь к малым поправкам (см. Изотопический сдвиг).

Обычно массу A. M выражают в атомных единицах массы (относит. масса А., см Атомная масса). Наиб. точные значения M получаются методами масс-спектроскопии.

Масса А. не равна в точности сумме масс ядра и электронов, а меньше её на величину дефекта масс, дефект масс для лёгких А. значительно меньше массы электрона, растёт с увеличением Z, но не превышает массы электрона даже для самых тяжёлых А.

А характеризуется полной энергией, выделяющейся при его образовании из ядра и электронов,- т. е. энергией связи, равной сумме энергий, необходимых для последоват. отрыва от ядра всех Z электронов. Полная энергия бистро возрастает с увеличением Z. Для тяжёлых А. она составляет неск. сотен кэВ (напр., для А. урана она 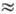400 кэВ).

Внутренняя энергия А.- его осн. характеристика. А. является квантовой системой, его внутр. энергия квантуется - принимает дискретный (прерывный) ряд значений, соответствующих устойчивым, стационарным состояниям А., промежуточные значения эта энергия принимать не может. На схемах уровней энергии возможные значения энергии А. изображаются горизонтальными линиями, расстояния между к-рыми пропорциональны соответствующим разностям энергий.

В простейшем случае А. водорода расстояния между уровнями энергии (рис. 1) закономерно уменьшаются и, бесконечно сгущаясь, уровни сходятся к границе ионизации 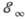, соответствующей отрыву электрона. Выше границы ионизации лежит непрерывный энергетич. спектр. Разность энергий 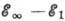есть энергия ионизации А. Схема уровней энергии водородоподобных ионов 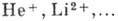отличается от приведенной на рис. только увеличением масштаба в Z² раз. Для А., содержащих 2 электрона и более, схемы уровней энергии усложняются.

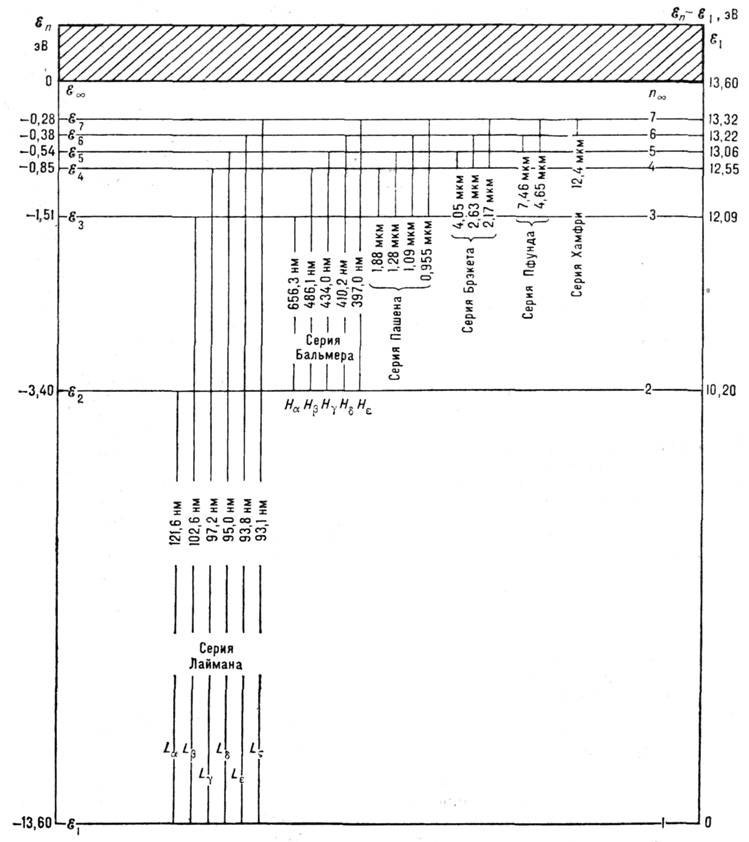
Рис. 1. Уровни энерг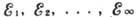ии А. водорода и квантовые переходы. Цифрами указаны длины волн спектральных линия, группирующихся в Спектральные серии. Для серий Лаймана и Бальмера даны обозначения отдельных линий.

Самый нижний (основной) уровень энергии А. соответствует состоянию А. с наименьшей энергией - его основному, или нормальному, состоянию; осн. состояние А. наиб. устойчиво, в нём свободный, не подверженный внеш. воздействиям А. может находиться неограниченно долго. Все остальные - возбуждённые - состояния А. обладают большей энергией. В возбуждённое состояние А. может перейти из основного путём излучательного квантового перехода, поглотив квант эл--магн. энергии, или получив энергию от др. частицы при столкновении с ней (безызлучательный квантовый переход).

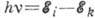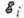Возбуждённые состояния имеют конечное время жизни (для свободного А. оно ~10^-8 с), т. к. А. стремится перейти в состояние с меньшей энергией; при этом А. испускает фотон, энергия к-рого равна , где и 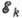- энергии верхнего и нижнего уровней А. соответственно, 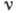- частота испускаемого эл--магн. излучения. При обратном переходе с нижнего уровня на верхний А. должна быть сообщена энергия 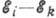. Каждому излучатель-ному квантовому переходу А. соответствует спектральная линия частоты 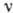(или длины волны 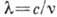), совокупность спектральных линий А. образует его спектр (см. А томные спектры). Интенсивность спектральных линий зависит от вероятностей соответствующих квантовых переходов, к-рые в свою очередь определяются т. н. Эйнштейна коэффициентами. (На рис. 1 показаны спектральные серии, в к-рые группируются спектральные линии А. водорода, для последних указаны длины волн .)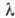

Значения дозволенных энергий А. можно определить, либо изучая возбуждение его электронным ударом - по значениям энергии возбуждающих электронов (потенциалов возбуждения), либо путём расшифровки атомных спектров; последний метод является основным для определения уровней энергии А., поскольку частоты 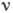испускаемых и поглощаемых фотонов определяются с гораздо большей точностью, чем потенциалы возбуждения.

Квантование энергии А. является следствием волновых свойств электрона, к-рыми он (как и др. микрочастицы) обладает наряду с корпускулярными свойствами (см. Корпускулярно-волновой дуализм ).Движению электрона в А. соответствует стоячая волна с длиной 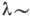10^-8 см, т. е. порядка линейных размеров А. Поскольку для стоячей волны в ограниченном объёме возможны лишь определ. значения 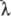, то и энергия А. также может принимать лишь дискретный ряд значений. Свободный электрон, оторванный от А., имеет непрерывный энергетич. спектр.

Теория атома водорода и водородоподобных ионов. Последовательная теория А. основана на законах квантовой механики. Квантовомеханич. теория объясняет устойчивость А., необъяснимую в рамках классич. физики, а также позволяет достаточно точно рассчитать для простейших А. уровни энергии, вероятности переходов и т. д., с помощью разл. приближённых методов можно рассчитывать характеристики сложных А. На основе квантовых представлений с единой точки зрения можно объяснить оптич., магн., электрич. и хим. (см. Квантовая химия)свойства А., а также периодическую систему элементов Менделеева.

Теорию одноэлектронного А.- А., состоящего из ядра с зарядом+Ze и одного электрона с зарядом -е, обычно наз. теорией А водорода. Движение электрона относительно ядра представляет собой движение частицы с тремя степенями свободы в кулоновском поле ядра (центр. поле). Потенциальная энергия электрона в таком поле 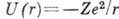, зависит только от расстояния r электрона от ядра и не зависит от направления радиуса-вектора. T. о., имеет место сферическая симметрия. Возможные значения энергии одноэлектронного А. (и соответствующие волновые функции, характеризующие состояние электрона в нём) получаются при решении Шрёдингера уравнения, в гамильтониан к-рого подставляется выражение для U(r). Когда энергия электрона отрицательна (для связанного электрона), возможные её значения задаются ф-лой:

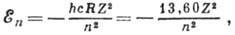
где n=1, 2, 3 ...-главное квантовое число, определяющее энергию различных состояний А., а постоянная hcR (R - Ридберга постоянная)представляет собой энергию ионизации А. водорода, равную энергии его основного состояния (Z=1, n = 1), взятой с обратным знаком.

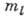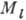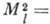
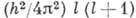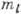Состояние А., кроме гл. квантового числа п, определяется также азимутальным (наз. также орбитальным) квантовым числом l и магн. квантовым числом . Квантовое число l = 0, 1, 2, ..., п - 1 определяет величину орбитального момента А., т. е. момента импульса электрона относительно ядра: . При заданном п число l принимает п разл. значений. 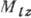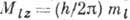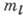Квантовое число определяет величину проекции орбитального момента на произвольно выбранное направление z: ; при заданном l число принимает 2l+1 значений: 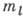- l, l - 1, ..., -l. Квантовые числа n, l и 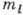полностью характеризуют состояние электрона в А. Состояния с l=0, 1, 2, 3, 4, 5, 6, ... принято обозначать буквами s, р, d, f, g, h, i, ... соответственно.

Точное положение электрона в А. в определ. момент времени установить нельзя вследствие неопределённостей соотношения. Состояние электрона в А. определяется волновой функцией 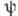, к-рая при заданных значениях п. l и 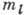определ. образом зависит от координат; 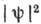даёт плотность вероятности нахождения электрона в данной точке пространства. Т.о., состояние электрона в А. можно характеризовать распределением в пространстве его электрич. заряда с некоторой плотностью - распределением электронной плотности 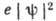(рис. 2). При этом электроны как бы размазаны в пространстве и образуют электронное облако, размеры к-рого растут ~ n². Для s-состояний (l=0) волновая функция и распределение электронной плотности обладают сферич. симметрией и обращаются в нуль на (n-1)-й сфере, то есть имеют п-1 узловую сферическую поверхность; при этом в центре (соответствующем началу координат) 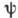и 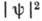отличны от нуля, что является характерной особенностью s-состояний; в точке, где находится ядро, вероятность нахождения электрона не равна нулю. Для р-состояний (l=1) и d-состояний (l=2) значения волновой функции и распределение электронной плотности в разных направлениях различны и зависят от абс. 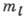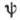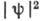значения ; при этом и обращаются в нуль на нек-рых узловых поверхностях и всегда равны нулю в начале координат.

В явном виде волновые функции получаются при решении ур-ния Шрёдингера:

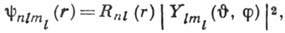
где 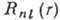- радиальная часть волновой функции, а 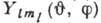- угловая часть, являющаяся сферической функцией. Электронная плотность

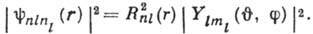
Вероятность найти электрон в элементе объёма

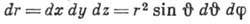
равна

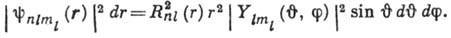
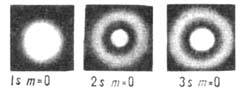
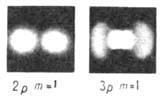
Рис. 2. Распределение электронной плотности в одноэлектронном атоме для состояний с п= 1,2 и 3, полученное фотографированием специальных моделей. При переходе от n=1 к n=2 и от п-2 к n=3 масштаб уменьшается.

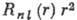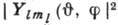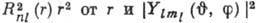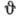Множитель определяет радиальное распределение электронной плотности - вероятность найти электрон на определ. расстоянии от ядра, рассчитанную на единицу длины; множитель определяет угловое распределение электронной плотности - зависимость от (от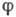 квадрат модуля сферич. функции не зависит, что приводит для состояния с заданным значением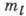 к распределению электронной плотности, обладающему аксиальной симметрией относительно выделенной оси).

Важным свойством состояний водородоподобного А. является независимость его энергии от l и 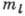. А. с определ. значением энергии может находиться в неск. состояниях с разл. значениями l и 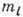, т. е. имеет место вырождение состояний (вырождение уровней энергии) А., причём число состояний с одинаковой энергией наз. степенью или кратностью вырождения. Независимость энергии А. от 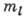(вырождение по m_l) связана со сферич. симметрией А. - энергия А. не зависит от значения проекции орбитального момента на произвольное направление, а независимость энергии от l (вырождение по l) связана с тем, что электрон в атоме движется в кулоновском поле ядра.

Для объяснения нек-рых явлений (напр., тонкой структуры, в атомных спектрах) теоретически был введён собств. момент импульса электрона - его спин (см. Дирака уравнение ),существование к-рого подтвердилось экспериментально Штерна - Герлаха опытом. Со спином электрона связан спиновый магн. момент электрона. Проекция спинового момента M_SZ электрона в А. на произвольную ось z определяется магн. спиновым (наз. также просто спиновым) квантовым числом 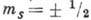: 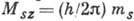. T. о., при заданных l и 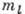возможны два разл. состояния А., отличающихся значениями 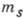. 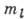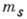Полная кратность вырождения по l, и равна .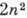

Для уровней энергии с п/2 вырождение снимается вследствие влияния спина на орбитальное движение электрона в А. - спин-орбитального взаимодействия - магн. взаимодействия магн. спинового момента электрона с его орбитальным магн. моментом, возникающим в результате орбитального движения электрона. Снятие вырождения приводит к расщеплению уровней энергии - появлению их тонкой структуры. Состояния А. характеризуются в этом случае полным моментом импульса 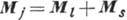. Величина 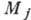определяется квантовым числом полного момента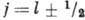 (иногда для него употребляют старый термин-внутр. квантовое число). В результате получается 2n - 1 состояний, отличающихся значениями l и j. При n = 1, 2, 3 получаются состояния:

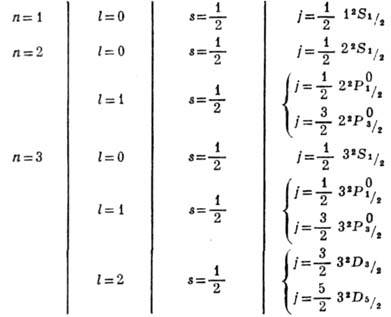
(обозначения в последнем столбце см. в ст. Атомные спектры).

Решение ур-ний квантовой механики с учётом спина электрона (релятивистская квантовая механика) приводит к изменению выражения для энергии - к ней добавляется величина

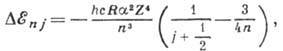
где 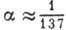-тонкой структуры постоянная .Зависимость 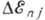от j приводит к расщеплению уровня энергии с заданным п на п подуровней. От l поправка 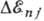не зависит, т. е. энергии состояний с одинаковыми j, но разными l должны быть равны. Величина расщепления уровней равна:

.

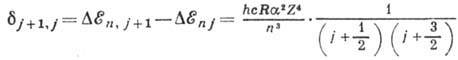Множитель 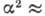1/18800, поэтому расщепление мало; так, для А. водорода при n= 2 величина 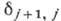получается равной 4,5*10^-5 эВ. С увеличением Z, абс. величина расщепления очень быстро растёт (как Z⁴, относит. величина расщепления).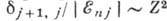

Исследования тонкой структуры спектральных линий и особенно непосредств. измерение расщепления уровней энергии А. водорода и гелия методами радиоспектроскопии с большой точностью подтвердили теоретически полученное выражение для 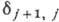. Опыт показал, что кроме расщепления наблюдается сдвиг уровней энергии - квантовый эффект, связанный с реакцией излучения. Наиб. точное определение сдвига уровней А. водорода, полученное методами радиоспектроскопии, показало, что расхождение опыта с теорией меньше 0,1%.

Наряду с тонкой наблюдается сверхтонкая структура уровней энергии, обусловленная взаимодействием магн. моментов электрона с магн. моментом ядра (см. Ядро атомное ),а также изотопич. смещение, связанное с различием масс ядер изотопов одного элемента. Нек-рое искажение сверхтонкой структуры возникает вследствие влияния квадрупольного электрич. момента ядра. Изучение всех этих малых эффектов спектроскопич. методами позволяет определять свойства и структуру атомных ядер. Для атома водорода сверхтонкая структура наблюдается и для основного уровня энергии (n=1, l=0; тонкая структура в этом случае отсутствует); это объясняется взаимодействием полного электронного момента атома 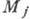со спиновым моментом ядра (протона). При переходе между двумя появляющимися подуровнями сверхтонкого расщепления основного уровня водорода возникает излучение с длиной волны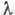=21 см, наблюдаемое для межзвёздного водорода.

Квантовомеханическая теория сложных атомов. Строение и свойства А., содержащих 2 и более электронов, значительно отличаются от теории водородоподобных атомов. Это объясняется прежде всего тем, что возникает необходимость учёта взаимодействий электронов друг с другом: электростатич. отталкивание и магн. взаимодействия спиновых и орбитальных магн. моментов электронов. Электростатич. взаимодействия электронов в А. велики по сравнению с магнитными. Они значительно ослабляют прочность связи электронов с ядром. Так, для А. гелия и гелиеподобных ионов Li⁺,Be²⁺, . . .) потенциальная энергия электронов: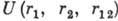

,

где r₁ и r₂ - расстояния 1-го и 2-го электронов от ядра, расстояние r_l2 между электронами определяет энергию их взаимодействия 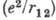, играющую весьма существ. роль; напр., энергия связи электрона в He⁺ равна 54,40 эВ, а энергия связи двух электронов в А. гелия в осн. состоянии - 78,98 эВ, т. е. меньше удвоенной энергии связи одного электрона в 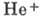, что объясняется отталкиванием электронов в Не.

Теория многоэлектронного А. должна учитывать принципиальную неразличимость и тождественность ого электронов (см. Тождественности принцип). Поэтому электронную оболочку сложного А. рассматривают как единую систему. При строгом квантовомеханич. рассмотрении сложный А. характеризуется волновой функцией, одинаково зависящей от координат всех электронов, антисимметричной относительно любой пары электронов, т. е. она должна менять знак при перестановке любых двух электронов (см. Паули принцип).

В грубом приближении можно считать, что каждый электрон в А. находится в своём квантовом состоянии, характеризуемом четырьмя квантовыми числами п, l, m_l и 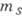, а состояние А. сводится к определ. сочетанию индивидуальных состояний отд. электронов. Тогда требование антисимметрии волновой функции А. может быть сведено к простейшей формулировке одного из осн. принципов для квантовой системы тождественных частиц - принципа Паули: в сложном А. в каждом из возможных квантовых состояний может находиться не более одного электрона, т. е. состояния электронов в А. должны отличаться хотя бы одним из 4 квантовых чисел п, l, m_l или 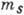. Характеристика состояний отд. электронов в сложном А. при помощи набора квантовых чисел позволяет систематизировать уровни энергии такого А.

В данном одноэлектронном состоянии энергия электрона оказывается зависящей не только от п, как в А. водорода, но и от l; от 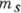и 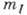она по-прежнему не зависит. Электроны с данными п и l, т.н. эквивалентные электроны, обладают одинаковой энергией и образуют электронную оболочку А.

Энергия отд. электрона в сложном А. может быть представлена в виде, аналогичном энергии А. водорода:

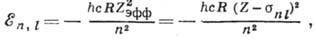
где 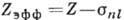, т. е. эфф. заряд, 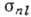- постоянная экранирования, приближённо учитывающая взаимодействие между электронами. T. о., электроны А. экранируют положительно заряж. ядро от рассматриваемого электрона. 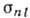возрастает с увеличением га, а при данном п - с увеличением l (чем больше l и п, тем дальше от ядра находится электрон и тем большее число электронов экранируют от него ядро). Электроны с меньшими значениями l связаны прочнее:

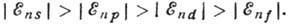
Выражение для 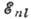соответствует предположению о том, что полное электрич. поле ядра и остальных электронов, действующее на данный электрон, обладает сферич. симметрией, как и кулоновское поле ядра в одноэлектронном А. Квантование орбитального момента импульса для многоэлектронного А. связано именно со сферич. симметрией электрич. поля, и квантовое число l сохраняет свой смысл.

Определение энергии А. с Z/2 и усреднённых полей, действующих на данный электрон со стороны остальных электронов, возможно лишь на основе приближённых квантовомеханич. методов расчёта. Так, для двух-электронного А. приближённое решение может быть получено с большой точностью путём применения вариационного метода. Приближённое квантовомеханич. решение для многоэлектронных А. может быть получено путём сведения его к задаче для одноэлектронной системы. В методе самосогласованного поля решается система ур-ний для движения каждого электрона в усреднённом поле всех остальных электронов; получающееся распределение электронной плотности отражает структуру электронных оболочек А. Хартри - Фока метод учитывает тождественность электронов.

Электронные оболочки атома. Периодическая система элементов. Индивидуальные состояния электронов в приближённой модели сложного А. группируются по значениям квантовых чисел n и l, причём число электронов в А. с заданными значениями п и l определяется принципом Паули. При заданном l магн. квантовое число m_l принимает 2l+1 значений, a m_S - два значения, поэтому число возможных состояний в электронной оболочке с данным l равно 2(2 l+1). Так, оболочка l=0 (s-оболочка) заполняется двумя электронами, оболочка l=1 (р-оболочка) - 6 электронами, оболочка l=2 (d-оболочка) - 10 электронами, оболочка l=3 (f-оболочка) - 14 электронами. Все электроны с заданным п образуют электронный слой, содержащий 2 п² электронов. Слои с n= 1,2,3,4,5,..., согласно терминологии, принятой для рентгеновских спектров, часто наз. K-, L-, M-, N-, P-слоями и т. д. Макс. число электронов в слое равно:

Рассматривая последовательное заполнение электронных слоев и оболочек, можно дать физ. объяснение пе-риодич. закона элементов Менделеева. Вблизи ядра А. находятся наиболее прочно связанные электроны с n=1, затем менее прочно связанные с n=2 и т. д. Соответственно этому происходит заполнение слоев при переходе от одного А. к другому, более тяжёлому. Так, у А. водорода и гелия имеются только один электронный слой и одна оболочка (n=1, l=0). При переходе к А. с большим Z, вследствие возрастания заряда ядра, электронный слой стягивается к ядру и начинает заполняться слой n=2 и т. д. При заданном п сначала заполняется состояния s-электронов (l=0), затем р-электронов (Z=1), d-электронов (l=2), f-электронов (n=3) и т. д. С точки зрения пространственного распределения, это означает, что сначала заполняются внутренние, более близкие к ядру слои, затем более внешние. При этом по мере возрастания Z внешние электронные оболочки периодически заполняются электронами с теми же значениями l (при возрастающих n); это приводит к периодичности хим. и физ. свойств элементов.

Периоды в периодич. системе элементов соответствуют последовательному заполнению электронных оболочек с возрастающими значениями n и l. Ядро с зарядом Z присоединяет электроны в порядке уменьшения прочности их связи. Для элементов 1-го периода происходит сначала заполнение оболочки 1 s, для элементов 2-го и 3-го периодов - оболочек 2 s, 2 р и 3 s, 3 р. Однако начиная с 4-го периода последовательность заполнения оболочек нарушается вследствие конкуренции близких по энергии связи электронов; при этом прочнее могут оказаться связанными электроны с большим n, но меньшим l (напр., электроны 4 s прочнее связаны, чем 3 d).

Распределение электронов в А. по оболочкам определяет его электронную конфигурацию. Для указания электронной конфигурации А. пишут в ряд символы заполненных электронных состояний оболочек, начиная с самой близкой к ядру; индексом справа вверху отмечают числа электронов в оболочке, находящихся в этих состояниях. Так, у атома Al (Z=13) в слое с n=1 имеются два s-электрона, в слое с n=2- два s- и шесть р-электронов, в слое с n=3 - два s- и один р-электрон. Это может быть записано в виде:

При 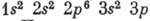заполнении 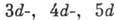-оболочек получаются группы переходных металлов, при заполнении 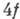- и 5f-оболочек - группа лантаноидов (редкоземельных элементов) и группа актиноидов (2-я группа редкоземельных элементов).

Порядок заполнения электронных оболочек при увеличении Z можно представить с помощью схемы:

В последующих оболочках электроны связаны менее прочно, чем в предшествующих, причём сначала заполняются оболочки с меньшими значениями n+l, а при том же значении n+l - с бблыпими значениями l (правило Клечковского).

Данная схема относится к последовательности заполнения внеш. оболочек А., что и определяет последовательность элементов в периодич. системе. При увеличении Z для внутр. оболочек восстанавливается нормальная последовательность оболочек по энергиям связи в них электронов, когда электроны с меньшим п связаны прочнее, чем электроны с большим п, независимо от значений l. Это происходит потому, что при возрастании Z разница в энергиях связи электронов с данным п, но разл. значениями l, становится менее существенной.

Наряду с нормальной электронной конфигурацией А., соответствующей наиб. прочной энергии связи всех электронов, при возбуждении одного или неск. электронов получаются возбуждённые электронные конфигурации. Каждой электронной конфигурации в случае полностью укомплектованных оболочек соответствует один уровень энергии А., а в случае недостроенных внутр. оболочек (напр., s, р, р², р³, sp,...) - ряд уровней энергии. Самый глубокий уровень энергии нормальной конфигурации А. наз. основным, все остальные уровни энергии - возбуждённые.

А. гелия имеет нормальную конфигурацию 1 s² и возбуждённые конфигурации 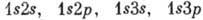, ,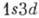 ... (возбуждён один электрон) и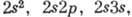 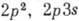, ... (возбуждены оба электрона). Нормальной электронной конфигурации и конфигурациям 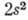, ,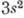 ..., содержащим электроны с одинаковым п и l=0, соответствует по одному уровню энергии, остальным конфигурациям - по нескольку уровней энергии. При этом все уровни энергии разбиваются на две системы уровней: систему уровней ортогелия и систему уровней парагелия; первая соответствует параллельной ориентации спинов электронов [спиновые моменты электронов 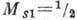и 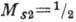(в единицах h)складываются в полный спиновый момент, равный 1], вторая - антипараллельной ориентации спинов (спиновые моменты компенсируются и полный спиновый момент равен нулю). Для нормальной конфигурации гелия 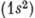вследствие принципа Паули возможна только антипараллельная ориентация спинов электронов, соответствующая парагелию.

Периодичность хим., оптич., электрич. и магн. свойств А. разл. элементов в зависимости от Z связана со сходным строением внеш. электронных оболочек, определяющим эти свойства. Эта периодичность сохраняется и для ионов: теряя один электрон, А. становится подобен по ряду свойств атомам предыдущей группы элементов (напр., однократно ионизованные щелочноземельные А.- атомам щелочных металлов). Сходными свойствами обладают члены изоэлектронного ряда. Совр. техника эксперимента позволяет получать многозарядные ионы тяжёлых элементов и исследовать их. Для таких высокоионизованных атомов 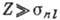и масштаб энергий возрастает ~Z².

Влияние на атом электрических и магнитных полей. А.- система электрически заряженных частиц, поэтому на него оказывают воздействие внеш. электрич. и магн. поля. Свободные А. не могут обладать постоянным электрическим дипольным моментом, но во внеш. электрич. поле они поляризуются - приобретают индуцированный дипольный момент (см. Поляризуемость атомов, ионов и молекул). Большинство А. обладают пост. магн. моментом, отличным от нуля и зависящим от того, как складываются спиновые и орбитальные моменты электронов. А. с целиком заполненными электронными оболочками, в частности А. инертных газов и щелочноземельных металлов, не имеют магн. момента, т. к. для любой заполненной оболочки все моменты (спиновые и орбитальные) отд. электронов при сложении компенсируются. А. с частично заполненными оболочками, как правило, имеют магн. моменты и являются парамагнитными (см. Парамагнетизм). Все А. обладают диамагнетизмом ,к-рый обусловлен появлением у них магн. момента под действием внеш. магн. поля.

Во внеш. поле А. приобретает дополнит. энергию и его уровни расщепляются, т. е. происходит снятие вырождения уровней энергии свободного А. кратности 2J+1, где квантовое число J определяет величину полного момента импульса А. В результате расщепления уровней энергии расщепляются и спектральные линии в спектре А. (см. Зеемана эффект, Штарка эффект). Магн. поле вызывает прецессию электронной оболочки вокруг направления поля (см. Лармора прецессия ).Дополнит. энергия, к-рую А. приобретает в магн. поле, зависит от абс. величины и знака квантового числа т_J, определяющего проекцию полного момента на некрое направление. T. к. т_J принимает 2J+1 значение, то уровень энергии в магн. поле расщепляется на 2J+1 подуровней.

Во внеш. электрич. поле дополнит. энергия, к-рую приобретает А., не зависит от знака 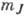, поэтому в электрич. поле происходит неполное расщепление уровней энергии - подуровни с 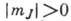дважды вырождены (уровень с 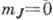невырожден).

На А., находящийся в связанном состоянии, существ. влияние оказывают неоднородные поля окружающих частиц. Особенно значительны воздействия электрич. полей, воздействия магн. полей играют меньшую роль. Уровни энергии ионов в кристалле или растворе могут сильно отличаться от уровней энергии свободного иона и терять дискретную структуру. Дискретная структура уровней может сохраняться в кристалле у ионов с достраивающимися d- и f-оболочками, действие на них полей окружающих частиц сводится к расщеплению уровней энергии, зависящему от симметрии поля. А., входящий в состав молекулы, ещё более отличается от свободного, т. к. внеш. электроны, определяющие осн. свойства А., участвуют в образовании хим. связи и лишь внутр. оболочки А. изменяются мало.

Для изучения свойств А. очень важно рассмотрение его поведения в газе и плазме, где действие на А. электрич. полей окружающих частиц приводит, в частности, к уширению спектральных линий.

Литература по физике атома

1. Шпольский Э. В., Атомная физика, т. 1, 7 изд., M., 1984;
2. Борн M., Атомная физика, пер. с англ., 3 изд., M., 1970;
3. Зоммерфельд А., Строение атома и спектры, пер. с нем., т. 1-2, M., 1956;
4. Давыдов А. С., Квантовая механика, 2 изд., M., 1973;
5. Фано У., Фано Л., Физика атомов и молекул, пер. с англ., M., 1980;
6. Moore C. E., Atomic energy levels, v. 1-3, Wash., 1949-58;
7. Bashkin S., Stoner J., Atomic energy level and grotrian diagrams, v. 1-3, Amst., 1975-81.

M. А. Ельяшевич

НОВОСТИ ФОРУМА Рыцари теории эфира

10.11.2021 - 12:37: ПЕРСОНАЛИИ - Personalias -> WHO IS WHO - КТО ЕСТЬ КТО - Карим_Хайдаров. 10.11.2021 - 12:36: СОВЕСТЬ - Conscience -> РАСЧЕЛОВЕЧИВАНИЕ ЧЕЛОВЕКА. КОМУ ЭТО НАДО? - Карим_Хайдаров. 10.11.2021 - 12:36: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ - Upbringing, Inlightening, Education -> Просвещение от д.м.н. Александра Алексеевича Редько - Карим_Хайдаров. 10.11.2021 - 12:35: ЭКОЛОГИЯ - Ecology -> Биологическая безопасность населения - Карим_Хайдаров. 10.11.2021 - 12:34: ВОЙНА, ПОЛИТИКА И НАУКА - War, Politics and Science -> Проблема государственного терроризма - Карим_Хайдаров. 10.11.2021 - 12:34: ВОЙНА, ПОЛИТИКА И НАУКА - War, Politics and Science -> ПРАВОСУДИЯ.НЕТ - Карим_Хайдаров. 10.11.2021 - 12:34: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ - Upbringing, Inlightening, Education -> Просвещение от Вадима Глогера, США - Карим_Хайдаров. 10.11.2021 - 09:18: НОВЫЕ ТЕХНОЛОГИИ - New Technologies -> Волновая генетика Петра Гаряева, 5G-контроль и управление - Карим_Хайдаров. 10.11.2021 - 09:18: ЭКОЛОГИЯ - Ecology -> ЭКОЛОГИЯ ДЛЯ ВСЕХ - Карим_Хайдаров. 10.11.2021 - 09:16: ЭКОЛОГИЯ - Ecology -> ПРОБЛЕМЫ МЕДИЦИНЫ - Карим_Хайдаров. 10.11.2021 - 09:15: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ - Upbringing, Inlightening, Education -> Просвещение от Екатерины Коваленко - Карим_Хайдаров. 10.11.2021 - 09:13: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ - Upbringing, Inlightening, Education -> Просвещение от Вильгельма Варкентина - Карим_Хайдаров.