Магнитные поверхностные уровни. РЕАЛЬНАЯ ФИЗИКА. Глоссарий по физике

Магнитные поверхностные уровни - квантовые энергетич. уровни электронов проводимости, движущихся в проводнике вблизи его поверхности под действием параллельного ей постоянного магн. поля. Для возникновения М. п. у. необходимы: большая длина свободного пробега электронов и большая вероятность их зеркального отражения при столкновенип с поверхностью проводника. Выполнение этих условии достигается при гелиевых температурах (4,2 К) в очень чистых монокристаллах проводников, имеющих оптически гладкую поверхность.

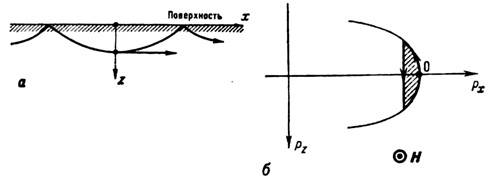
Рис. 1, а - траектория электрона, "скачущего" внутри проводника по его поверхности под действием силы Лоренца, создаваемой магнитным полем; б - траектория "скачущего" электрона в импульсном пространстве; показано сечение поверхности Ферми плоскостью рисунка; О - опорная точка.

Квазиклассич. картина явления состоит в следующем. М. п. у. возникают в проводнике для электронов, фермиевская скорость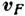

к-рых почти параллельна поверхности образца. В пространстве импульсов эти электроны находятся на ферми-поверхности в малой окрестности её т. н. опорной точки О, в к-рой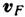

точно параллельна поверхности образца. Магн. поле, воздействуя на электроны этой группы силой Лоренца, удерживает их у поверхности образца. В этих условиях электроны движутся по дугам малой кривизны, возвращаясь к поверхности образца и зеркально отражаясь от неё. Тем самым электроны совершают периодич. движение (электроны "скачут" по поверхности, рис. 1, а), к-рое должно быть квантовано. Разрешёнными оказываются орбиты, для к-рых магн. поток через сегмент, образуемый дугой траектории и поверхностью образца, равен

где n=1, 2, ..., е - элементарный заряд. В импульсном пространстве движению по скачущим орбитам соответствует движение по замкнутой орбите на поверхности Ферми в малой окрестности точки О (рис. 1, б), к-рое квантуется.

Квантовое рассмотрение движения электронов приводит к выражению для значений магн. поля Я_пь при к-рых имеют место максимумы резонансного поглощения эл--магн. поля частоты

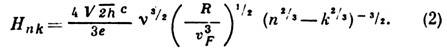
Здесь п, k=1, 2, 3, ...;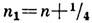

;

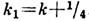; R - радиус кривизны орбиты электронов в точке О.

Экспериментально существование М. п. у. обнаруживается как осцилляции (с амплитудой

0,1%) полного поверхностного сопротивления проводника (

10-100 ГГц) в зависимости от магн. поля, изменяющегося в пределах 0,1-100 Э (рис. 2). М. п. у. изучались на монокристаллах Sn, Bi, In, Cd, Al, Cu [1, 2]. Природа осцилляции аналогична эффекту де Гааза - ван Альфена (см. Квантовые осцилляции в магнитном поле). Вычисленные по ф-ле (2) и по известным параметрам поверхности Ферми Bi значения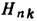

точно совпадают с измеренными максимумами реактивного поверхностного сопротивления образца Bi [3-5].

Ф-ла (2) верна для образцов с плоской поверхностью; если же образец имеет цилиндрич. поверхность, то спектр

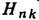изменяется. Наблюдается смещение и уширение линий спектра [6]. К изменению ширины и амплитуды линий приводит также изменение состояния поверхности образца (полировка, травление и др.).

Рис. 2, а - измеренные осцилляции поверхностного сопротивления (реактивного X)образца Bi при температуре 1,7 К на частоте 9,7 Ггц; б - рассчитанный спектр значений

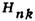поля резонансного поглощения излучения электронами, находящимися на магнитных поверхностных уровнях.

В образце сверхпроводника первого рода в магн. поле, меньшем критического, существует лишь один М. п. у. нормальных электронов. Положение и ширина единств. линии поглощения определяется характером проникновения магн. поля в поверхностный слой сверхпроводника [7].

Исследование М. п. у. даёт возможность измерять параметры поверхности Ферми, изучать распределение магн. поля в поверхностном слое проводника и характер взаимодействия электронов с его поверхностью.

Литература по магнитным поверхностным уровням

Знаете ли Вы, почему "черные дыры" - фикция?
Согласно релятивистской мифологии, "чёрная дыра - это область в пространстве-времени, гравитационное притяжение которой настолько велико, что покинуть её не могут даже объекты, движущиеся со скоростью света (в том числе и кванты самого света). Граница этой области называется горизонтом событий, а её характерный размер - гравитационным радиусом. В простейшем случае сферически симметричной чёрной дыры он равен радиусу Шварцшильда".
На самом деле миф о черных дырах есть порождение мифа о фотоне - пушечном ядре. Этот миф родился еще в античные времена. Математическое развитие он получил в трудах Исаака Ньютона в виде корпускулярной теории света. Корпускуле света приписывалась масса. Из этого следовало, что при высоких ускорениях свободного падения возможен поворот траектории луча света вспять, по параболе, как это происходит с пушечным ядром в гравитационном поле Земли.
Отсюда родились сказки о "радиусе Шварцшильда", "черных дырах Хокинга" и прочих безудержных фантазиях пропагандистов релятивизма.
Впрочем, эти сказки несколько древнее. В 1795 году математик Пьер Симон Лаплас писал:
"Если бы диаметр светящейся звезды с той же плотностью, что и Земля, в 250 раз превосходил бы диаметр Солнца, то вследствие притяжения звезды ни один из испущенных ею лучей не смог бы дойти до нас; следовательно, не исключено, что самые большие из светящихся тел по этой причине являются невидимыми." [цитата по Брагинский В.Б., Полнарёв А. Г. Удивительная гравитация. - М., Наука, 1985]
Однако, как выяснилось в 20-м веке, фотон не обладает массой и не может взаимодействовать с гравитационным полем как весомое вещество. Фотон - это квантованная электромагнитная волна, то есть даже не объект, а процесс. А процессы не могут иметь веса, так как они не являются вещественными объектами. Это всего-лишь движение некоторой среды. (сравните с аналогами: движение воды, движение воздуха, колебания почвы). Подробнее читайте в FAQ по эфирной физике.