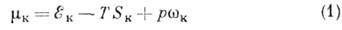
Кристаллизация - образование кристаллов из газа, раствора, расплава, стекла или кристалла др.
структуры (полиморфные превращения). К. состоит в укладке атомов, молекул или
ионов в кристаллическую решётку. К. определяет образование минералов,
льда, играет важную роль в атм. явлениях, в живых организмах (образование зубной
эмали, костей, почечных камней). Путём К. получают и массивные монокристаллы,
и тонкие кристаллич. плёнки полупроводников, диэлектриков и металлов. Массовая
К.- одноврем. рост множества мелких кристаллов - лежит в основе металлургии
и широко используется в хим., пищевой и медицинской промышленности.
Термодинамика кристаллизации. Расположение частиц в кристалле упорядочено (см. Дальний и ближний порядок), и их энтропия SK меньше энтропии Sc в неупорядоченной
среде (паре, растворе, расплаве). Поэтому снижение температуры Т при пост.
давлении р ведёт к тому, что химический потенциал вещества в кристалле
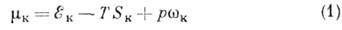
становится меньше его потенциала
в исходной среде:
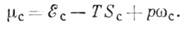
Здесь 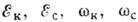 - энергии взаимодействия частиц и уд. объём вещества в кристаллич. и неупорядоченном
состояниях (фазах), SK и SС - энтропии. Т. о., кристаллич. фаза оказывается "выгоднее", происходит К.,
сопровождаемая выделением т.н. скрытой теплоты К.:
- энергии взаимодействия частиц и уд. объём вещества в кристаллич. и неупорядоченном
состояниях (фазах), SK и SС - энтропии. Т. о., кристаллич. фаза оказывается "выгоднее", происходит К.,
сопровождаемая выделением т.н. скрытой теплоты К.: 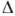 H=T(SC-SK)
H=T(SC-SK)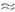 0,5-5
эВ, а также скачком уд. объёма
0,5-5
эВ, а также скачком уд. объёма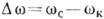 (фазовый переход первого рода). Если р
(фазовый переход первого рода). Если р 104
атм, то член
104
атм, то член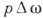 в соотношении (1) мал, и при
в соотношении (1) мал, и при теплота
К. равна
теплота
К. равна 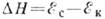 ,
т. е. является мерой изменения энергии связи между частицами при К. [при К.
из расплава
,
т. е. является мерой изменения энергии связи между частицами при К. [при К.
из расплава 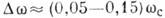 и может иметь разл. знаки].
и может иметь разл. знаки].
К. при полиморфных превращениях
(см. Полиморфизм)может быть фазовым переходом второго рода. В случае
переходов первого рода граница раздела кристалл - среда локализована в пределах
неск. межатомных расстояний, и её уд. свободная энергия 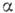 >0.
>0.
Для переходов 2-го рода
граница не локализована и
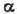 =0.
=0.
Условия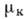 (р,
Т, Ск) =
(р,
Т, Ск) =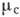 (р,
Т, Сс) для каждого из компонентов кристалла и среды определяют
связь р, Т и концентрации компонентов С, при к-рых кристалл
находится в равновесии со средой, т. е. диаграмму состояния вещества.
Разность
(р,
Т, Сс) для каждого из компонентов кристалла и среды определяют
связь р, Т и концентрации компонентов С, при к-рых кристалл
находится в равновесии со средой, т. е. диаграмму состояния вещества.
Разность 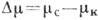 , являющаяся мерой отклонения от равновесия, наз. термодинами ч. движущей силой
К. Обычно она создаётся понижением температуры ниже равновесного значения Т0, т.е. переохлаждением системы на
, являющаяся мерой отклонения от равновесия, наз. термодинами ч. движущей силой
К. Обычно она создаётся понижением температуры ниже равновесного значения Т0, т.е. переохлаждением системы на 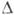 Т-Т0-Т. Если
Т-Т0-Т. Если
 Т
Т  Т0, то
Т0, то

Если давление р паров
или концентрация С в растворе больше равновесных значений р0 и С0, то говорят об абс. пересыщении (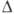 р=р-
р0 или
р=р-
р0 или  С=С-С0)
либо относит. пересыщении (
С=С-С0)
либо относит. пересыщении (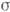 =
= р/р0 или
р/р0 или  С/С0).
В этом случае в разреженных парах и разведённых растворах
С/С0).
В этом случае в разреженных парах и разведённых растворах
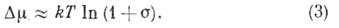
В процессе выращивания
монокристаллов из растворов обычно 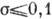 , из паров и при хим. реакциях
, из паров и при хим. реакциях 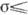 1,
при конденсации молекулярных пучков
1,
при конденсации молекулярных пучков 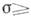 102-104.
102-104.
К. может происходить в
результате или с участием хим. реакций. Равновесное состояние смеси газов при
возможной хим. реакции между составляющими её веществами Ai можно
обобщённо записать в виде 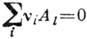 , где
, где 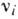 - стехиометрич. коэф. (
- стехиометрич. коэф. (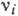 <0
для прямой реакции,
<0
для прямой реакции,
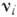 >0
- для обратной). В этом случае
>0
- для обратной). В этом случае
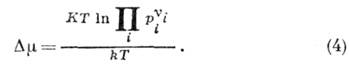
Здесь К - константа
равновесия реакции, рi - парциальные давления (или концентрации,
если реакция протекает в растворе). В случае электролитов

где Ze - заряд иона
(Z - ат. номер), 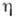 -
отклонение разности потенциалов между кристаллом и раствором от равновесного
значения.
-
отклонение разности потенциалов между кристаллом и раствором от равновесного
значения.
Зародыши кристаллизации.
Пересыщенная или переохлаждённая фаза может сохранять своё состояние чрезвычайно
долго (К. не идёт). Такое состояние наз. метастабилъным. Расплавы чистых металлов
переохлаждаются на 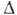 Т= (0,3-0,5) Т0, вода - на
Т= (0,3-0,5) Т0, вода - на 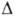 Т
Т
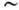 40 К
40 К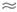 0,15
T0, пары - до s
0,15
T0, пары - до s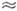 10,
растворы - до
10,
растворы - до 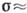 3. Стёкла могут быть охлаждены до ОК (см. Аморфное состояние ).Загрязнённые
среды кристаллизуются на посторонних частицах (центры К.) при небольших
3. Стёкла могут быть охлаждены до ОК (см. Аморфное состояние ).Загрязнённые
среды кристаллизуются на посторонних частицах (центры К.) при небольших 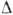 Т. Критич. переохлаждение
Т. Критич. переохлаждение 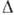 Т зависит также от температуры, материала и состояния стенок сосуда, действия
излучений. Причина такой устойчивости - в трудности зарождения кристаллов. Атомы
и молекулы газа или жидкости могут при соударениях соединяться в агрегаты из
2, 3 и т. д. частиц. Часть их распадается вследствие флуктуации колебат. энергии
частиц. Если кол-во частиц N в агрегате охватывает 2-4 координац. сферы,
то к нему можно применять макроскопич. понятия поверхностной энергии и хим.
потенциала и др. Ат. структура зародышей пока недостаточно выяснена. Однако
есть данные о том, что она может отличаться от структуры устойчивой макроскопической
фазы.
Т зависит также от температуры, материала и состояния стенок сосуда, действия
излучений. Причина такой устойчивости - в трудности зарождения кристаллов. Атомы
и молекулы газа или жидкости могут при соударениях соединяться в агрегаты из
2, 3 и т. д. частиц. Часть их распадается вследствие флуктуации колебат. энергии
частиц. Если кол-во частиц N в агрегате охватывает 2-4 координац. сферы,
то к нему можно применять макроскопич. понятия поверхностной энергии и хим.
потенциала и др. Ат. структура зародышей пока недостаточно выяснена. Однако
есть данные о том, что она может отличаться от структуры устойчивой макроскопической
фазы.
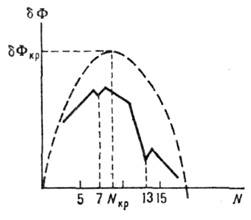
Рис. 1. Работа образования
зародыша кристаллизации 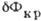 как функция числа частиц в нём Nkp для феноменологической (пунктир)
и микроскопической (сплошная линия) моделей.
как функция числа частиц в нём Nkp для феноменологической (пунктир)
и микроскопической (сплошная линия) моделей.
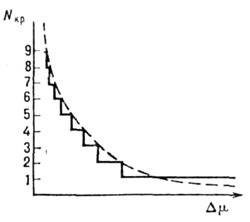
Рис. 2. Зависимость числа частиц в критическом зародыше Nkp от переохлаждения для феноменологической (пунктир) и микроскопической (сплошные линии) моделей.
Переохлаждение в однородной
гомогенной фазе определяется работой образования границы раздела при появлении
кристаллич. фазы внутри материнской. Эта работа положительна, если удельная
свободная энергия границы 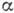 >0.
Образование агрегата новой кристаллич. фазы из N частиц с поверхностью
>0.
Образование агрегата новой кристаллич. фазы из N частиц с поверхностью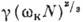 увеличивает термодинамич. потенциал Ф системы на величину, равную
увеличивает термодинамич. потенциал Ф системы на величину, равную 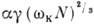 , где число
, где число 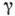 зависит от формы агрегата. Одновременно Ф уменьшается на
зависит от формы агрегата. Одновременно Ф уменьшается на 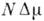 ,
т. к. новая фаза "выгоднее"
старой
,
т. к. новая фаза "выгоднее"
старой 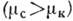 . В результате работа образования зародыша
. В результате работа образования зародыша 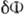 =
=
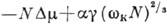 достигает
максимума
достигает
максимума 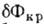 =
=
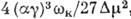 , когда
размер зародыша приобретает критич. значение Nkp=
, когда
размер зародыша приобретает критич. значение Nkp= (рис. 1). Работа образования критич. зародыша
(рис. 1). Работа образования критич. зародыша 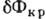 минимальна для кристалликов равновесной формы, у к-рых минимальна поверхностная
энергия при данном объёме. Критич.
зародыши образуются
в результате тепловых флуктуации. Увеличение степени отклонения от равновесия
минимальна для кристалликов равновесной формы, у к-рых минимальна поверхностная
энергия при данном объёме. Критич.
зародыши образуются
в результате тепловых флуктуации. Увеличение степени отклонения от равновесия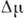 уменьшает работу образования зародыша. Скорость зарождения
уменьшает работу образования зародыша. Скорость зарождения
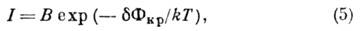
где В пропорционально
плотности частиц в среде и скорости их присоединения к критич. зародышу (в очищенных
парах и растворах В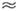 1025-1030
см-3с-1, в расплавах В
1025-1030
см-3с-1, в расплавах В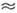 1037-1042
см-3 с-1). Число частиц в критич. зародыше убывает с переохлаждением
(в расплаве Ga при
1037-1042
см-3 с-1). Число частиц в критич. зародыше убывает с переохлаждением
(в расплаве Ga при 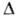 T=0,5
Т0, Nkp
T=0,5
Т0, Nkp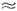 10
атомов, радиус зародыша r3
10
атомов, радиус зародыша r3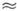 4
А). Т. к. Nkp не может меняться меньше чем на 1, то существуют интервалы
изменения
4
А). Т. к. Nkp не может меняться меньше чем на 1, то существуют интервалы
изменения 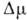 , в пределах к-рых Nkp постоянно (рис. 2). Эти интервалы малы
в области умеренных пересыщении, но проявляются при больших, напр. в условиях
конденсации молекулярных пучков и электролитич. осаждения, когда Nkp
, в пределах к-рых Nkp постоянно (рис. 2). Эти интервалы малы
в области умеренных пересыщении, но проявляются при больших, напр. в условиях
конденсации молекулярных пучков и электролитич. осаждения, когда Nkp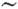 1-10.
В результате зависимости
1-10.
В результате зависимости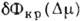 и I (
и I (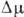 )
становятся ломаными линиями (рис. 1).
)
становятся ломаными линиями (рис. 1).
К зародышам из неск. атомов
понятие поверхностной энергии не применимо, и описание зарождения ведётся на
конкретных микроскопич. моделях. Однако для оценок можно пользоваться феноменологич.
представлениями, дающими несколько заниженную скорость зарождения (рис. 1, 2).
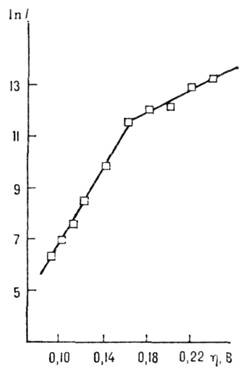
Рис. 3. Скорость зарождения
In I на аморфном углероде при электролитической кристаллизации в зависимости
от перенапряжения h: левая прямая отвечает первому атому в зародыше, правая
- второму.
Упаковка частиц в малых
зародышах может не совпадать с упаковкой в массивном кристалле, напр. обнаружено
неск. метастабильных фаз в каплях Ga и Вr, замёрзших при глубоких переохлаждениях.
Масс-спектральный анализ агрегатов в парах Pb и в Хе обнаружил повышение
содержания кластеров из 7, 13, 19 и т. д. атомов, характерных для некристаллографич.
пентагональной упаковки (рис. 4). Поверхностные атомы в этих кластерах образуют
завершённую координац. сферу. Поэтому работа их образования минимальна, а их
число максимально по сравнению с зародышами, содержащими на 1 атом больше или
меньше.
Образование зародыша на
хорошо смачиваемой поверхности кристалла требует преодоления меньшего барьера,
и потому такое гетерогенное зарождение происходит при меньших переохлаждениях
(см. Эпитаксия).

Рис. 4. Кристаллографическая
плотнейшая (вверху) и пентагональная (внизу) упаковки.
Понижение температуры не только
уменьшает работу образования зародыша, но и экспоненциально повышает вязкость
расплава, т. е. снижает частоту присоединения новых частиц к зародышу (рис.
5, а). В результате I(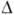 Т)сначала достигает максимума, а затем становится столь малой (рис. 5, б), что при низких темп-pax расплав затвердевает, оставаясь аморфным. В расплавах
со сравнительно малой вязкостью это возможно лишь при очень быстром (
Т)сначала достигает максимума, а затем становится столь малой (рис. 5, б), что при низких темп-pax расплав затвердевает, оставаясь аморфным. В расплавах
со сравнительно малой вязкостью это возможно лишь при очень быстром ( 106
К/с) охлаждении. Так получают аморфные сплавы металлов (см. Аморфные металлы). В жидком гелии образование зародышей возможно не переходом системы через
барьер, а туннельным просачиванием сквозь него. При выращивании крупных совершенных
кристаллов на "затравках" избегают появления спонтанных зародышей,
используя слабо пересыщенные растворы или перегретые расплавы. Наоборот, в металлургии
стремятся получить максимальное число центров К., создавая глубокие переохлаждения
(см. ниже).
106
К/с) охлаждении. Так получают аморфные сплавы металлов (см. Аморфные металлы). В жидком гелии образование зародышей возможно не переходом системы через
барьер, а туннельным просачиванием сквозь него. При выращивании крупных совершенных
кристаллов на "затравках" избегают появления спонтанных зародышей,
используя слабо пересыщенные растворы или перегретые расплавы. Наоборот, в металлургии
стремятся получить максимальное число центров К., создавая глубокие переохлаждения
(см. ниже).
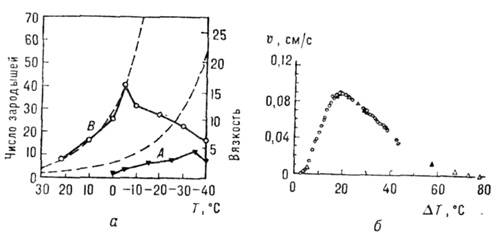
Рис. 5. Температурные зависимости
скорости зарождения и роста кристалла: а) сплошные кривые - температурная зависимость
числа зародышей цитриновой кислоты в переохлаждённом водном растворе
(температуры насыщения: А-62 °С, В - 85 °С); пунктир - увеличение
вязкости (в пуазах) растворов с понижением Т; б) скорость роста v кристаллов бензофенона из расплава как функции  Т.
Т.
Рост кристалла может
быть послойным и нормальным в зависимости от того, является ли его поверхность
в атомном масштабе
гладкой или шероховатой. Атомные плоскости, образующие гладкую грань, почти
полностью укомплектованы и содержат сравнительно небольшое число вакансий и атомов, адсорбированных в местах, соответствующих узлам кристаллич. решётки
следующего слоя. Края незавершённых атомных плоскостей образуют ступени (рис.
6, в). В результате тепловых флуктуации ступень содержит нек-рое число трёхмерных
входящих углов - изломов. Присоединение новой частицы к излому не изменяет энергии
поверхности и поэтому является элементарным актом роста кристалла. С увеличением
отношения тепловой энергии kT к поверхностной энергии 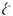 (в расчёте на 1 атомное место на поверхности) плотность изломов увеличивается.
Соответственно увеличивается конфигурац. энтропия и падает свободная линейная
энергия ступени. При определ. отношениях
(в расчёте на 1 атомное место на поверхности) плотность изломов увеличивается.
Соответственно увеличивается конфигурац. энтропия и падает свободная линейная
энергия ступени. При определ. отношениях 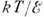 (близких к 1, но несколько различных для разных граней) линейная энергия ступени
обращается в 0, и ступень "размазывается" по грани, к-рая превращается
в шероховатую, т. е. равномерно и плотно покрытую изломами поверхность (рис.
6, б). Связь поверхностной энергии с теплотой К. позволяет заключить,
что для веществ и температур, для к-рых изменение энтропии при К. таково, что
(близких к 1, но несколько различных для разных граней) линейная энергия ступени
обращается в 0, и ступень "размазывается" по грани, к-рая превращается
в шероховатую, т. е. равномерно и плотно покрытую изломами поверхность (рис.
6, б). Связь поверхностной энергии с теплотой К. позволяет заключить,
что для веществ и температур, для к-рых изменение энтропии при К. таково, что 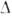 S/k>4,
все плотноупакованные грани - гладкие. Эта ситуация характерна для равновесия
кристалл - пар, а также (для нек-рых веществ) для границы кристалл -расплав.
Переход от шероховатости к огранению возможен при изменении концентрации в двухкомпонентных
системах (К. из растворов). Если
S/k>4,
все плотноупакованные грани - гладкие. Эта ситуация характерна для равновесия
кристалл - пар, а также (для нек-рых веществ) для границы кристалл -расплав.
Переход от шероховатости к огранению возможен при изменении концентрации в двухкомпонентных
системах (К. из растворов). Если  S/k<2 (типично для плавления металлов), то поверхности любой ориентации шероховаты.
При
S/k<2 (типично для плавления металлов), то поверхности любой ориентации шероховаты.
При 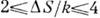 отдельные
гладкие грани сосуществуют с шероховатыми поверхностями (напр., кристаллы Ge
и Si в расплавах, гранаты в расплавах и высокотемпературных растворах). Зависимость
свободной энергии и скорости К. от ориентации поверхности имеет острые (сингулярные)
минимумы для гладких (сингулярных) граней и округлённые (несингулярные) для
шероховатых поверхностей.
отдельные
гладкие грани сосуществуют с шероховатыми поверхностями (напр., кристаллы Ge
и Si в расплавах, гранаты в расплавах и высокотемпературных растворах). Зависимость
свободной энергии и скорости К. от ориентации поверхности имеет острые (сингулярные)
минимумы для гладких (сингулярных) граней и округлённые (несингулярные) для
шероховатых поверхностей.
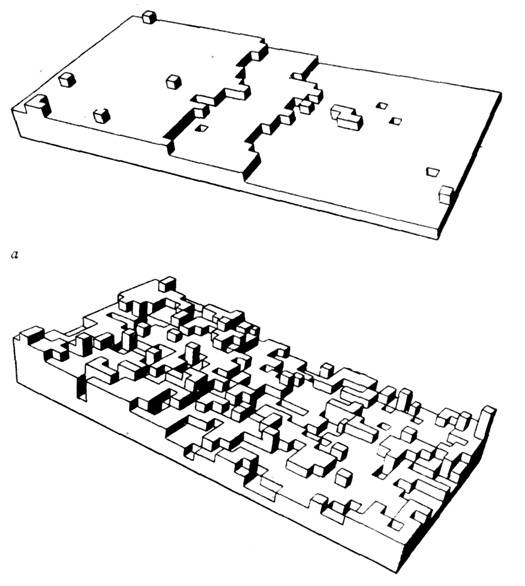
Рис. 6. Атомно-гладкая
(а) и шероховатая (б) поверхности (моделирование на ЭВМ).

Рис. 7. Концентрические ступени на грани (100) NaCl при росте из молекулярного пучка. Высота ступени 2,82 А (декорированы мелкими кристалликами специально осаждённого золота).
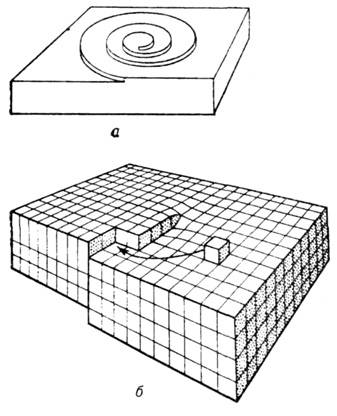
Рис. 8. а - Спиральная форма роста; б - ступень, оканчивающаяся на поверхности в точке её пересечения винтовой дислокацией.
Присоединение нового атома
в любом положении на поверхности кроме излома меняет её энергию. Заполнение
немногочисленных вакансий, снижающее эту энергию, не может дать начала новому
атомному слою, а концентрация атомов в местах, соответствующих узлам решётки
следующего слоя, повышает энергию и поэтому мала. В результате необратимое присоединение
частиц к кристаллу, т. е. его рост, возможен только когда на его поверхности
есть изломы. На шероховатых поверхностях плотность изломов велика, и рост вдоль
нормали к поверхности возможен практически в любой точке. Такой
рост наз. нормальным. Он лимитируется скоростью присоединения отд. частиц к
изломам. Его скорость R линейно увеличивается с переохлаждением на фронте
К.:
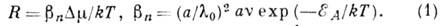
Здесь а - межатомное
расстояние,l0 - расстояние между изломами, 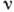 - эффективная частота тепловых колебаний,
- эффективная частота тепловых колебаний, 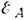 -
энергия, необходимая для присоединения частиц к излому (энергия активации).
Она учитывает перестройку ближнего порядка в жидкости, десольватацию строит.
частиц и изломов в растворах, хим. реакции и т. д. В простых расплавах коэф.
-
энергия, необходимая для присоединения частиц к излому (энергия активации).
Она учитывает перестройку ближнего порядка в жидкости, десольватацию строит.
частиц и изломов в растворах, хим. реакции и т. д. В простых расплавах коэф.
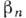 велики,
что обеспечивает рост
с заметной скоростью, когда переохлаждение на фронте К.
велики,
что обеспечивает рост
с заметной скоростью, когда переохлаждение на фронте К. 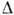 Т
Т 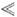 1К.
Так, для роста Si
1К.
Так, для роста Si 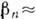 106 см/с R= (3-5)*10-3 см/с достигается при
106 см/с R= (3-5)*10-3 см/с достигается при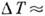 10-5 К. При достаточно низких темп-pax подвижность частиц падает
и скорость роста уменьшается, подобно скорости зарождения (рис. 5, б).
10-5 К. При достаточно низких темп-pax подвижность частиц падает
и скорость роста уменьшается, подобно скорости зарождения (рис. 5, б).
Если поверхность гладкая,
то изломы существуют только на ступенях, рост идёт последоват. отложением слоев
и наз. послойным. Если поверхность образована лестницей одинаковых ступеней
и в среднем отклонена от ближайшей сингулярной грани на угол с тангенсом р, то ср. скорость её роста вдоль нормали к этой сингулярной ориентации

где 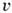 - скорость роста ступени вдоль грани,
- скорость роста ступени вдоль грани,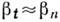 (В растворах
(В растворах 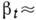 10-1-10-3
см/с.)
10-1-10-3
см/с.)
Плотность ступеней определяется
тем, генерируются ли они двумерными зародышами или дислокациями .Образование
двумерных зародышей требует преодоления потенциального барьера, высота к-рого
пропорциональна линейной энергии ступеней и обратно пропорциональна 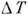 .
Соответственно, скорость К. экспоненциально мала при малых
.
Соответственно, скорость К. экспоненциально мала при малых 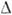 Т [для роста грани (III) Si с R=(3-5)*10-3 см/с необходимо
Т [для роста грани (III) Si с R=(3-5)*10-3 см/с необходимо 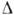 Т
Т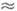 0,ЗК;
см. выше]. При К. из молекулярных пучков, если есть места преимущественного
образования двумерных зародышей, ступени имеют вид замкнутых колец (рис. 7).
Возможно, что образование зародышей "облегчается" точками выхода
на поверхность краевых дислокаций.
0,ЗК;
см. выше]. При К. из молекулярных пучков, если есть места преимущественного
образования двумерных зародышей, ступени имеют вид замкнутых колец (рис. 7).
Возможно, что образование зародышей "облегчается" точками выхода
на поверхность краевых дислокаций.
При росте на винтовой дислокации,
образуемая ею ступень в процессе роста приобретает спиральную форму (рис. 8),
т. к. в точке окончания ступени на дислокации её скорость роста равна 0. В процессе
спирального роста новый слой "накручивается" сам на себя вокруг
точки выхода дислокации и на поверхности возникает пологий (вицинальный) холмик
роста. Часто холмики образуются группой дислокаций, суммарный вектор Бюргерса
к-рых имеет в направлении нормали к поверхности составляющую Ь, равную
неск. параметрам а решётки. Точки выхода этих дислокаций могут занимать
на поверхности некоторую область (с периметром
2L, рис. 9, а, в). В этом случае склон кругового вицинального
холмика образует с сингулярной гранью угол с тангенсом р =b/(19rc
+2h) (рис. 9,б). Наклоны холмиков измеряются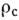 методами
оптич. интерферометрии (рис. 10), методом цветов тонких пластинок, а иногда
непосредственно визуализацией ступеней.
методами
оптич. интерферометрии (рис. 10), методом цветов тонких пластинок, а иногда
непосредственно визуализацией ступеней.
-
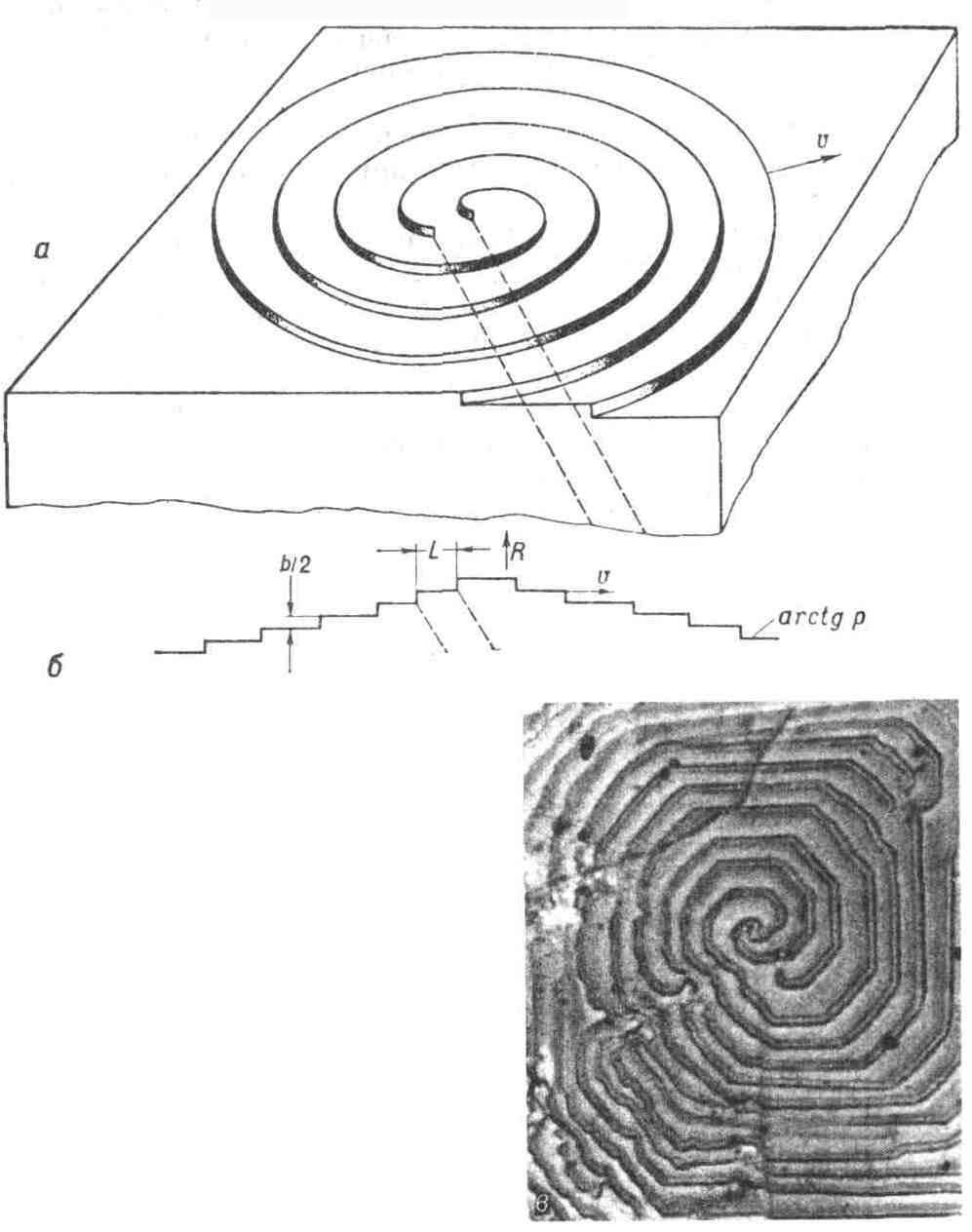
Рис. 9. Двухзаходная спираль,
образующая вицинальный холмик вокруг точек выхода на поверхность двух дислокаций:
о) общий вид холмика; б) его сечение плоскостью, перпендикулярной грани и проходящей
через точки выхода дислокаций; в) спираль на грани (100) синтетического алмаза.

Рис. 10. Интерференционные
полосы от вицинального холмика на грани призмы кристалла ADP (рост из
водного раствора).
Радиус двумерного критяч.
зародыша 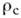 пропорционален линейной энергии ступени и обратно пропорционален
пропорционален линейной энергии ступени и обратно пропорционален  Т. Поэтому с увеличением
Т. Поэтому с увеличением 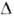 Т крутизна холмика р линейно увеличивается при малых
Т крутизна холмика р линейно увеличивается при малых  Т и стремится к насыщению при больших (при L
Т и стремится к насыщению при больших (при L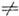 0).
Соответственно, нормальная скорость роста R квадратично увеличивается
с пересыщением
0).
Соответственно, нормальная скорость роста R квадратично увеличивается
с пересыщением 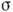 при
малых переохлаждениях и линейно - при больших (рис. 11). Вариации вектора
Бюргсрса и протяжённость
L дислокац. источника определяют разброс значений скорости роста кристаллографически
идентичных граней (или одной и той же грани) в одинаковых условиях. В процессе
роста грани точка выхода не перпендикулярной ей дислокации смещается и может
достигнуть одного из рёбер. После этого ступень исчезает. Дальше К. идёт лишь
путём двумерного зарождения, и скорость роста при малых переохлаждениях
падает (по крайней мере в неск. раз при К. из расплава и на неск. порядков при
К. из раствора). Из-за относительно малых значений линейной энергии ступеней
на границе кристалл - расплав и отсутствия проблемы доставки кристаллизующегося
вещества
при
малых переохлаждениях и линейно - при больших (рис. 11). Вариации вектора
Бюргсрса и протяжённость
L дислокац. источника определяют разброс значений скорости роста кристаллографически
идентичных граней (или одной и той же грани) в одинаковых условиях. В процессе
роста грани точка выхода не перпендикулярной ей дислокации смещается и может
достигнуть одного из рёбер. После этого ступень исчезает. Дальше К. идёт лишь
путём двумерного зарождения, и скорость роста при малых переохлаждениях
падает (по крайней мере в неск. раз при К. из расплава и на неск. порядков при
К. из раствора). Из-за относительно малых значений линейной энергии ступеней
на границе кристалл - расплав и отсутствия проблемы доставки кристаллизующегося
вещества 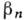 ,
,
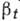 и Л
на неск. порядков выше, чем для К. из растворов и газовой фазы.
и Л
на неск. порядков выше, чем для К. из растворов и газовой фазы.
Ввиду малой плотности газовой
фазы послойная К. из неё идёт в осн. не прямым попаданием частиц на ступени,
а за счёт диффузии частиц, адсорбированных на атомно-гладких "террасах"
между ступенями. За время между моментами прилипания к поверхности и десорбции
такая частица совершает случайные блуждания по поверхности и уходит от точки
прилипания на расстояние порядка ср. длины диффузионного пробега ls.
Поэтому достичь ступени могут лишь частицы, адсорбировавшиеся вокруг неё в полосе
шириной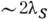 Большинство частиц, падающих на поверхность с малой плотностью ступеней, испаряются
- коэф. конденсации для таких поверхностей мал. Он приближается к 1 при большой
плотности ступеней, т. е. при значит. пересыщениях. По той же причине скорость
К. из газовой фазы даже на одной дислокации квадратично увеличивается с пересыщением
при малых пересыщениях и линейно - при больших. При конденсации молекулярных
пучков ступени образуются путём двумерного зарождения в местах, где пересыщение
в адсорбционном слое достигает критического, и потому ср. расстояние между ступенями
определяется длиной пробега адсор-биров. частиц.
Большинство частиц, падающих на поверхность с малой плотностью ступеней, испаряются
- коэф. конденсации для таких поверхностей мал. Он приближается к 1 при большой
плотности ступеней, т. е. при значит. пересыщениях. По той же причине скорость
К. из газовой фазы даже на одной дислокации квадратично увеличивается с пересыщением
при малых пересыщениях и линейно - при больших. При конденсации молекулярных
пучков ступени образуются путём двумерного зарождения в местах, где пересыщение
в адсорбционном слое достигает критического, и потому ср. расстояние между ступенями
определяется длиной пробега адсор-биров. частиц.
Подвод вещества к растущей
поверхности и отвод от неё теплоты К. ограничивает скорость К., когда эти процессы
протекают медленнее поверхностных. Такой диффузионный режим типичен для К. из
расплавов и неперемешиваемых растворов. Высокая скорость К. из расплава лежит
в основе всех широко используемых методов выращивания монокристаллов, в к-рых
скорость К. задаётся механич. движением кристалла относительно независимо формируемого
теплового поля. Кинетич. режим К., когда скорость К. лимитируется поверхностными
процессами, характерен для К. из перемешиваемых растворов, из газовой фазы и
роста из перемешиваемого расплава кристаллов с высокой энтропией плавления.
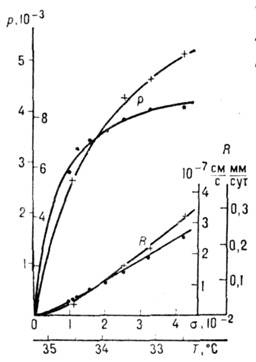
Рис. 11. Наклоны р вицинальных
холмиков, образованных двумя разными дислокационными источниками, и задаваемые
ими скорости роста грани R в зависимости от пересыщения 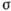 .
.
Формы роста кристаллов
(габитус) определяются анизотропией скорости К. и условиями тепло- и массопереноса.
Кристаллы с шероховатыми поверхностями имеют обычно округлую форму. Атомно-гладкие
поверхности проявляются в виде граней. Стационарная форма кристаллич. многогранника
такова, что расстояние от центра до каждой грани пропорционально её скорости
роста. В результате кристалл оказывается образованным гранями с мин. скоростями
роста (грани с большими скоростями постепенно уменьшаются и исчезают). Они параллельны
плоскостям с наиб. плотной упаковкой и наиб. сильными связями в атомной структуре
кристалла. Поэтому кристаллы с цепочечной и слоистой структурой имеют игольчатую
или таблитчатую форму. Анизотропия скоростей роста и, следовательно, форма роста
кристалла в разл. фазах зависят от состава, Т, 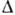 Т и сильно меняются под действием поверхностно-активных примесей.
Т и сильно меняются под действием поверхностно-активных примесей.
Из-за большой скорости
поверхностных процессов К. переохлаждение  Т на атомно-шероховатых поверхностях мало, т. е. Т=Т0 (отсюда
назв. изотермы). Плотноупакованные грани с простыми индексами в случае неметаллов
часто остаются сингулярными и появляются на округлом фронте К. в виде плоского
среза в форме круга, эллипса или кольца (рис. 12, а) в зависимости от формы
изотермы К. Темп-ра вдоль такой грани не постоянна и достигает минимума в точках,
наиб. удалённых от изотермы Т=Т0. В этих точках наивысшего
переохлаждения генерируются слои, определяющие скорость роста грани. Поэтому
стационарный размер грани тем больше, чем большее
Т на атомно-шероховатых поверхностях мало, т. е. Т=Т0 (отсюда
назв. изотермы). Плотноупакованные грани с простыми индексами в случае неметаллов
часто остаются сингулярными и появляются на округлом фронте К. в виде плоского
среза в форме круга, эллипса или кольца (рис. 12, а) в зависимости от формы
изотермы К. Темп-ра вдоль такой грани не постоянна и достигает минимума в точках,
наиб. удалённых от изотермы Т=Т0. В этих точках наивысшего
переохлаждения генерируются слои, определяющие скорость роста грани. Поэтому
стационарный размер грани тем больше, чем большее  Т нужно для её роста со скоростью, равной скорости округлого фронта К.
в направлении вытягивания кристалла. Шероховатые и гранные поверхности захватывают
разные кол-ва примесей, и кристалл с сосуществующими гранными и шероховатыми
формами вырастает неоднородным (рис. 12, б).
Т нужно для её роста со скоростью, равной скорости округлого фронта К.
в направлении вытягивания кристалла. Шероховатые и гранные поверхности захватывают
разные кол-ва примесей, и кристалл с сосуществующими гранными и шероховатыми
формами вырастает неоднородным (рис. 12, б).
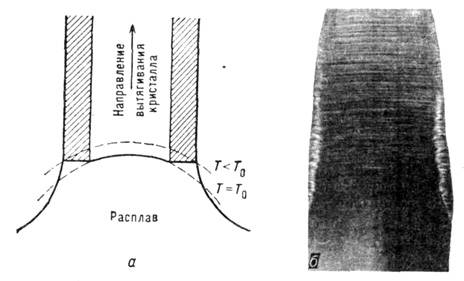
Рис. 12. Образование плоской
грани на округлом фронте кристалла (кристалл вытягивается из расплава): а
- осевое сечение кристалла с фронтом кристаллизации, вогнутым в сторону кристалла
в центре и плоским по периферии; б-продольное сечение кристалла Si (периферич.
область обогащена примесью).
Если Т в расплаве убывает по мере удаления от фронта К., то фронт неустойчив: случайно возникший на нём выступ попадает в область большего переохлаждения, скорость роста вершины выступа становится ещё больше и т. д. В результате плоский фронт распадается на прилегающие друг к другу пластинчатые или игольчатые кристаллы - в сечении, параллельном фронту, возникает полосчатая или ячеистая структура. Ячейки характерны для больших градиентов температуры и имеют обычно гексагональную форму независимо от симметрии кристалла (рис. 13). Неустойчивость не совместима с выращиванием совершенных монокристаллов, т. к. ведёт к захвату включений маточной среды. Сферич. кристалл, растущий в переохлаждённом расплаве или растворе, сохраняет свою форму, пока его радиус не достигнет критич. значения, зависящего от радиуса критич. зародыша и скорости поверхностных процессов К. В дальнейшем развиваются выступы, и кристалл приобретает скелетную (рис. 14, а, б)или дендритную форму (рис. 14, в, г). Название последней связывается с появлением вторичных ветвей после достижения первичным выступом критич. длины.
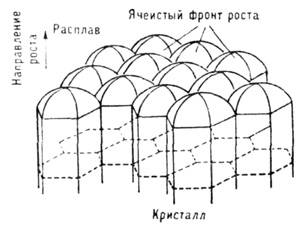
Рис. 13. Схема ячеистой
структуры фронта кристаллизации.
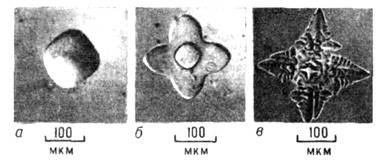
Рис. 14. Исходный округлый кристалл циклогексанола в расплаве (а), начальная стадия роста скелетного кристалла (б), дендрит (в), дендрит при большом переохлаждении (г).
Примесь, отталкиваемая
фронтом К. из расплава, скапливается перед ним и, меняя равновесную температуру
К., вызывает т. н. концентрац. переохлаждение, увеличивающееся по мере удаления
от фронта. Если равновесная темп-pa в расплаве увеличивается с расстоянием от
фронта быстрее, чем истинная, то возникает концентрационная неустойчивость.
Она исчезает при достаточно высоких отношениях градиента температуры на фронте К.
к его скорости.
Фронт К. из раствора всегда
неустойчив, т. к. пересыщение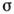 увеличивается
по мере удаления от растущей поверхности. Для огранённых кристаллов характерно
большое пересыщение около вершин и рёбер, причём перепад
увеличивается
по мере удаления от растущей поверхности. Для огранённых кристаллов характерно
большое пересыщение около вершин и рёбер, причём перепад 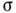 увеличивается
с размером грани. При достаточно больших пересыще-нии и размере грани вершины
становятся ведущими источниками ступеней роста, а в центр. частях граней возникают
провалы - начинается скелетный рост (рис. 15). Ему способствуют нек-рые примеси.
Неустойчивость К. из растворов подавляется интенсивным перемешиванием, снижением
пересыщения, а иногда введением примесей.
увеличивается
с размером грани. При достаточно больших пересыще-нии и размере грани вершины
становятся ведущими источниками ступеней роста, а в центр. частях граней возникают
провалы - начинается скелетный рост (рис. 15). Ему способствуют нек-рые примеси.
Неустойчивость К. из растворов подавляется интенсивным перемешиванием, снижением
пересыщения, а иногда введением примесей.

Рис. 15. Скелетный кристалл шпинели.
Захват примесей. Отношение
концентраций примеси в кристалле и исходном веществе наз. коэф. захвата К. При К<1 К. ведёт к очистке от примеси кристалла, при К>1 - к очистке
исходной среды, К=1 соответствует сохранению концентрации. Коэф. захвата разными
гранями различны и не совпадают с термоди-намич. равновесными, определяемыми
диаграммой состояния. Поэтому состав кристалла отклоняется от термодинамически
равновесного. Так, при лазерной или электронной импульсной рекристаллизации
тонких приповерхностных слоев Si со скоростями К. до
неск. м/с концентрация
примесей As, Sb, In, Bi в кристалле Si превосходит равновесную в 3-600 раз,
причём подавляющее большинство примесных атомов находится в узлах решётки. Это
связано, во-первых, со статистич. отбором: каждый узел решётки при К. окончательно
заполняется тем или иным атомом после множества попыток (от 106-107
при скоростях 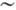 10-3
см/с и до 10 при скоростях
10-3
см/с и до 10 при скоростях 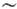 м/с).
Во-вторых, в условиях быстрой К. не успевает протекать диффузия в расплаве.
м/с).
Во-вторых, в условиях быстрой К. не успевает протекать диффузия в расплаве.
Неравновесный захват примеси
при послойном росте связан со статистич. отбором на ступенях, а также с тем,
что даже равновесная концентрация примеси в поверхностном слое кристалла и торце
ступени заметно отличается от объёмной. При достаточно быстром отложении слоев
следующий слой замуровывает предыдущий вместе с содержащейся в нём примесью.
В результате каждая грань захватывает примесь в кол-ве, отвечающем концентрации
в её поверхностном слое, и кристалл оказывается сложенным из секторов роста
разных граней, с разл. концентрациями примесей и др. дефектов - возникает
т. н. секториальное строение кристалла (рис. 16). Количество примеси, захватываемое
при движении ступени по грани, зависит от ориентации этой ступени. Поэтому сектор
роста данной грани, в свою очередь, разбивается на области, отложенные вициналями разной ориентации с разным содержанием примеси (вицинальная секториальность,
рис. 17).
Темп-pa и концентрация
примеси на фронте К. из расплава флуктуируют из-за конвекции расплава и вращения
кристалла и тигля в обычно слегка несимметричном тепловом поле. Соответствующие
положения фронта К. отпечатываются в кристалле в виде полос (зонар-ное строение,
рис. 16). Флуктуации температуры могут быть столь сильны, что рост кристалла сменяется
плавлением и ср. скорость оказывается на порядок меньше мгновенной. Интенсивность
конвекции и амплитуда полосчатости уменьшаются при выращивании кристаллов в
невесомости.

Рис. 16. Секториальное
и зонарное строение кристалла алюмокалиевых
квасцов.
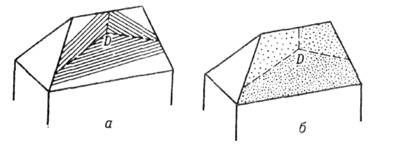
Рис. 17. Вицинальный холмик,
образованный на грани ступенями трёх разных ориентации вокруг краевой дислокации
D(a). Разные склоны холмика захватывают разные количества примеси (б).
Образование дефектов.
Посторонние газы, растворимые в растворах и расплавах лучше, чем в кристаллах,
выделяются на фронте К. Пузырьки газа захватываются растущим кристаллом, если
они превышают критич. размер, убывающий с увеличением скорости роста (аналогично
захватываются твёрдые частицы). При К. в невесомости конвективный отвод пузырьков
от фронта К. затруднён и кристалл обогащается газовыми включениями. Специально
создавая пузырьки, получают пеноматериалы. Реальные кристаллы всегда имеют зонарно
и секториально распределённые примеси, к-рые изменяют параметр решётки, что
вызывает внутр. напряжения, дислокации и трещины. Последние возникают также
из-за несоответствия параметров решёток затравки (подложки) и нарастающего на
ней кристалла. Источниками внутр. напряжений и дислокаций
являются также включения маточной среды и посторонних частиц.
При К. из расплава дислокации
возникают из-за термоупругих напряжений, вызванных нелинейным распределением
температуры; при охлаждении уже выросших частей кристалла снаружи; при линейном
распределении температуры вдоль нормали к достаточно протяжённому фронту К., если
свободный температурный изгиб кристалла невозможен; наследованием из затравки.
Поэтому выращивание бездислокационных кристаллов Si, GaAs, IP начинают с затравок
малого диаметра и ведут в максимально однородном температурном ноле. Кристаллы
могут содержать петли дислокаций размером меньше 1 мкм. Петли образуются как
контуры дискообразных скоплений (кластеров) межузельных атомов (или вакансий),
возникших в результате распада пересыщенного твёрдого раствора при охлаждении
выросшего кристалла. Атомы примеси могут быть центрами зарождения кластеров.
Массовая К. При
определ. условиях возможен одноврем. рост множества кристаллов. Спонтанное массовое
появление зародышей и их рост происходят, напр., при затвердевании отливок металлов.
Кристаллы зарождаются прежде всего на охлаждаемых стенках изложницы, куда заливается
перегретый металл. Зародыши на стенках ориентированы хаотично, однако в процессе
роста "выживают" те из них, у к-рых направление макс. скорости роста
перпендикулярно стенке (геометрич. отбор кристаллов). В результате у поверхности
возникает т.н. столбчатая зона, состоящая из узких кристаллов, вытянутых вдоль
нормали к поверхности.
Массовая К. в растворах начинается либо на спонтанно возникших зародышах, либо на специально введённых затравках. Сталкиваясь в перемешиваемом растворе между собой, со стенками сосуда и мешалкой, кристаллики разрушаются и дают начало новым центрам К. (вторичное зарождение). Причиной вторичного зарождения могут быть также мелкие обломки нависающих над гранью слоев, "запечатывающих" плоские параллельные грани, включения маточного раствора. В металлургии используют сильные конвективные потоки, обламывающие дендритные кристаллы и разносящие центры К. по всему объёму, иногда применяют УЗ-дробление растущих кристаллов. Массовой К. очищают вещества от примеси (К<1). Массовая К. из газовой фазы (в т. ч. из плазмы) используется для получения ультрадисперсных порошков с размерами кристалликов до 10-6 см и менее. Необходимые для этого высокие переохлаждения достигаются резким охлаждением пара смеси химически реагирующих газов или плазмы. Известен способ массовой К. капель, кристаллизующихся во время падения в охлаждаемом газе.

А. А. Чернов
|
|