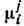каждого компонента i во всех фазах j:Диаграмма состояния (фазовая диаграмма) - диаграмма, изображающая зависимость устойчивого фазового
состояния одно- или многокомпонентного вещества от термодинамич. параметров,
определяющих это состояние (температуры T, давления P, напряжённостей
магн. H или электрич. E полей, концентрации с и др.). Каждая
точка Д. с. (фигуративная точка) указывает на фазовый состав вещества при заданных
значениях термодинамич. параметров (координатах этой точки). В зависимости от
числа внеш. параметров Д. с. может быть двумерной, трёхмерной и многомерной.
При исследовании равновесия фаз в условиях перем. давления строят изобарич.
и изоконцентрац. сечения и проекции на плоскости T-P или Р-с. Наиб.
полно изучены изобарич. Т-с сечения Т-Р-с Д. с., соответствующие
атм. давлению.
Устойчивому состоянию системы
при заданных T и P соответствует минимум Гиббса энергии системы
G. Из этого условия вытекают ур-ния равновесия, определяющие границы
фаз на Д. с. Ур-ние фазового равновесия однокомпонентного вещества выражается
равенством мольных энергий Гиббса этих фаз; в дифференц. форме - это Клапейрона-Клаузиуса
уравнение. Ур-ния равновесия многокомпонентной системы сводятся к равенству
хим. потенциалов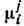
каждого компонента i во всех фазах j:
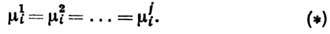
Анализ системы ур-ний (*)
приводит к Гиббса правилу фаз. Это правило определяет наиб. число фаз,
к-рые могут находиться в равновесии, и число независимых параметров (степеней
свободы), изменение к-рых не нарушает фазового состояния вещества. Нонвариантному
равновесию (0 степеней свободы) соответствуют на Д. с. точки, одновариантному
- линии, двухвариантному - участки плоскости и т. д.
Д. с. однокомпонентного
вещества обычно строится на плоскости в координатах T-P, T-V, P-V, T-H и
др. Темп-pa равновесия двух фаз однокомпонентного вещества при заданном давлении
определяется точкой пересечения кривых G(T)этих фаз (рис. 1). В тройных
точках пересекаются три кривые попарного
равновесия фаз, эти точки соответствуют равновесию трёх фаз. Равновесие большего
числа фаз невозможно. Кривая равновесия двух фаз может оканчиваться в критической
точке.
Для двухкомпонентных веществ
система ур-ний (*) геометрически соответствует условиям общего касания к кривым
G(с) (рис. 2) сосуществующих фаз;
точки касания определяют структуру и составы фаз, находящихся в равновесии при
заданных условиях. Концентрации фаз в двухфазном состоянии определяют с помощью
конод (изотермич. прямых на изобарич. сечениях, соединяющих точки фазовых границ;
см. рис. 3, а). Относит. количества фаз в двухфазном состоянии определяются
правилом рычага.
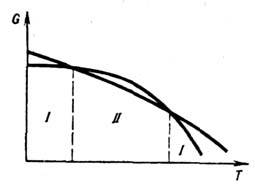
Рис. 1. Зависимость энергии
Гиббса G двух
фаз I и II от температуры.
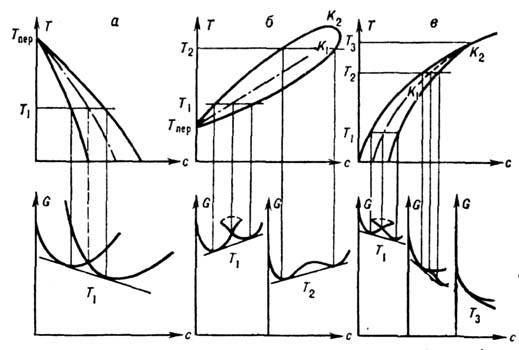
Рис. 2. Участки диаграммы состояния разных типов (вверху) и соответствующие им кривые G(с).
При фазовых переходах 2-го рода правило фаз Гиббса неприменимо, поэтому на T-с Д. с. такие
фазы не всегда разделяются двухфазными областями, в отличие от переходов 1-го
года (см. рис. 2,в, выше K2).
На рис. 2 показаны участки
Д. с. разных типов и соответствующие им кривые G(с). На рис. 2, а изображено равновесие
фаз с разными структурами, на рис. 2, б - равновесие изоструктурных фаз
с критич. точками изоконцентрационного превращения К1 ирасслоения
K2; на рис. 2, в - переход порядок-беспорядок с двумя
критич. точками изоконцентрац. перехода K1 (трикритич. точка)
и расслоения K2. Когда фазы имеют разную структуру
(рис. 2, а), каждой из них соответствует своя зависимость G(C),
а в случае изоструктурных фаз (рис. 2, б)и переходов типа порядок -беспорядок
(рис. 2, в) обе фазы описываются единой зависимостью G(с) (одной
кривой с "петлёй" и без неё). Знание положения линий Т0(с)
- линий равных энергий Гиббса обеих фаз одного и того же состава (см. штриховые
линии на рис. 2) - важно в тех случаях, когда из-за малой диффузионной подвижности
реализуются изоконцентрац. ("бездиффузионные") превращения (см.
Мартенситное превращение, Кристаллизация). При отсутствии пересечения
линий G(c) (рис. 2, б, в при T>TK1)
изоконцентрац. равновесия нет. В интервале TK1<Т<TK2
имеет место расслоение, аналогичное расслоению жидких и твёрдых растворов.
На рис. 2, в (Т>TK1)на кривых G(C) имеется
точка ветвления, соответствующая фазовому переходу 2-го рода.
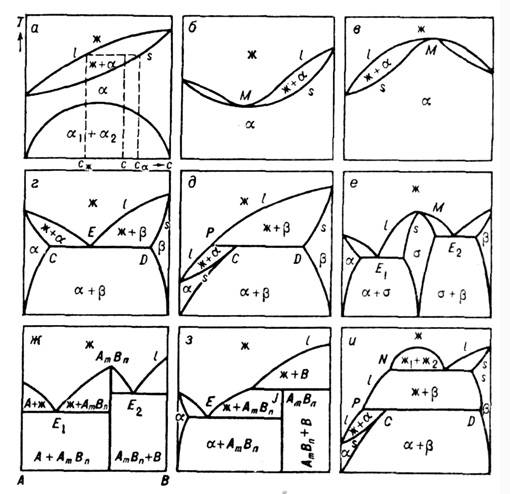
Рис. 3. Диаграммы состояний
разных типов в координатах T-с: ж - жидкая фаза,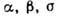
- твёрдые фазы, AmBn - хим. соединение компонентов,
С, D - тройные точки, E, E1, E2 - эвтектические
точки, M - точки максимума и минимума, P - перитектическая точка.
Д. с. могут иметь разнообразную
форму (рис. 3). К одному типу могут быть отнесены Д. с., на к-рых сохраняются
неизменными число, размерность и взаимное расположение всех геом. элементов
(характерных точек, линий, областей). Форма и размер отрезков линий и областей
могут изменяться при сохранении типа Д. с. К характерным точкам относятся: критич.
точки, точки фазовых переходов 2-го рода, трикритич. точки, точки равных концентраций
с максимумом или минимумом M (рис. 3, б, в, е), точки равновесия
трёх фаз (тройные точки на Д. с. однокомпонентного вещества), эвтектическая
E (рис. 3, г), перитектическая P (рис. 3 д, и),
монотектическая (рис. 3, и)точки, точка инконгруэнтного плавления соединения
J (рис. 3, з). К характерным точкам можно также отнести точки
фазовых переходов компонентов и соединений (в последнем случае при наличии сингулярной
точки Д. с. разбивается на две: см. рис. 3, ж), точки максимумов и минимумов
на их кривых плавления. На одной Д. с. может быть неск. характерных точек. Появление
или исчезновение одной из них меняет тип Д. с. Эволюция T-с изобарич.
сечений Т-Р-с Д. с. при изменении давления может привести к смене типов
этих сечений (рис. 4) при переходе через граничные (переходные) Д. с. (рис.
4, б, д).
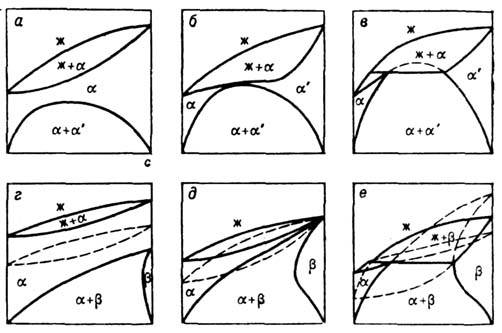
Рис. 4. Эволюция изобарических
сечений диаграммы состояний двухкомпонентного вещества: а, б, в - простейшие
Д. с., г, д,е - сложные. Пунктиром показаны метастабильные диаграммы
состояний или их участки: ж - жидкая фаза,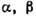 
- твёрдые фазы.
Д. с. трёхкомпонентного
вещества при пост. P трёхмерна. Система координат, в к-рой она изображается,
представляет собой рёбра трёхгранной призмы, основанием к-рой служит концентрац.
треугольник; ось T перпендикулярна основанию, а грани являются Д. с.
бинарных систем.
На плоскости строят изотермич.
(рис. 5), политермич. и квазибинарные сечения трёхмерной Д. с. Политермическими
наз. сечения плоскостью, параллельной оси T. Квазибинарными - Д. с. систем,
компонентами к-рых являются соединения, образующиеся в двух бинарных системах,
или соединение и один из компонентов. Относит. количества фаз, находящихся в
равновесии, определяются правилом центра тяжести. Как и правило рычага, оно
следует из условия сохранения количества каждого компонента. Д. с. n-компонентной
системы при перем. T и P - (n+1)-мерны. Для их изображения
разрабатывают спец. методы.
Рис. 5. Изотермическое
сечение диаграммы состояний трёхкомпонентного вещества в случае ограниченной
растворимости в твёрдых растворах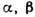 
и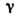
Имеется ряд ограничений
на структуру Д. с. Так, согласно третьему началу термодинамики, при T=0
К энтропия S=0, откуда вытекает неустойчивость растворов при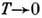 
К, они должны расслаиваться на смеси компонентов, соединений и стехиометрически
упорядоченных фаз. Однако из-за малой диффузионной подвижности при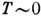 
К в большинстве случаев полного расслоения растворов наблюдать не удаётся. Границы
равновесия двух фаз могут сливаться только в точках превращений чистых компонентов
или в точках минимума или максимума этих границ.
Д. с., как правило, являются
сложными и могут быть расчленены на простейшие. Д. с. на рис. 4, а-в являются
простейшими. Д. с. на рис. 4, г-е расчленяются на три простейшие:
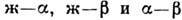, к-рые полностью
или частично метастабильны. Д. с. одного и того же типа может быть как простейшей,
так и сложной (ср. рис. 4, в, е). На Д. с. рис. 4, а-в
можно нанести только одну линию T0(с)изоконцентрац. равновесия,
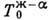; на Д. с. рис.
4, г-е три такие линии: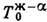 
,
. При изменении
давления (или смене одного из компонентов) простейшие Д. с., составляющие сложную,
смещаются относительно друг друга, что приводит к стабилизации одних участков
Д. с. и дестабилизации других. Тип простейших Д. с. определяется термодинамич.
свойствами компонентов в сосуществующих фазах и термодинамич. свойствами растворов.
Для построения Д. с. используют
данные разл. методов: рентгеноструктурного, калориметрического, термического,
дилатометрического, оптич. и электронной микроскопии, ЯМP и др.
Д. с. можно рассчитать,
если известны аналитич. выражения для G(T,P,с)всех фаз, образующихся
в данной системе. Для определения вида G(T, P, с)достаточно иметь эксперим.
данные о термодинамич. свойствах системы. Однако обычно такие данные либо отсутствуют,
либо неполны. Для конструирования G(T, P, с)используют поэтому теорию
растворов, электронную теорию вещества, разл. рода эмпирич. и полуэмпирич. соотношения.
Привлекают закономерности изменения свойств элементов с изменением их атомного
номера и положения в таблице Менделеева, а также имеющиеся данные об известных
участках Д. с., метастабильных фазах в рассматриваемой системе, её физ. свойствах.
Наиб. перспективным путём построения Д. с. является оптим. сочетание всех методов
(эксперим. и теоретич.) нахождения функций G(T, P, с) и последующего расчёта
с помощью ЭВМ.
Д. с. используют на практике
в материаловедении, металлургии, металловедении, химии, геологии и др.
И. Л. Аптекарь, Д. С. Каменецкая
Дело в том, что в его постановке и выводах произведена подмена, аналогичная подмене в школьной шуточной задачке на сообразительность, в которой спрашивается:
- Cколько яблок на березе, если на одной ветке их 5, на другой ветке - 10 и так далее
При этом внимание учеников намеренно отвлекается от того основополагающего факта, что на березе яблоки не растут, в принципе.
В эксперименте Майкельсона ставится вопрос о движении эфира относительно покоящегося в лабораторной системе интерферометра. Однако, если мы ищем эфир, как базовую материю, из которой состоит всё вещество интерферометра, лаборатории, да и Земли в целом, то, естественно, эфир тоже будет неподвижен, так как земное вещество есть всего навсего определенным образом структурированный эфир, и никак не может двигаться относительно самого себя.
Удивительно, что этот цирковой трюк овладел на 120 лет умами физиков на полном серьезе, хотя его прототипы есть в сказках-небылицах всех народов всех времен, включая барона Мюнхаузена, вытащившего себя за волосы из болота, и призванных показать детям возможные жульничества и тем защитить их во взрослой жизни. Подробнее читайте в FAQ по эфирной физике.
|
|
 |
