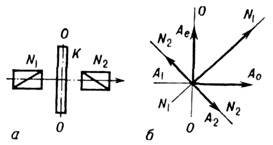
Рис. 1. Наблюдение интерференции поляризованных лучей в параллельных лучах:
а - схема; б - определение амплитуд колебаний, соответствующих схеме а.
Интерференция поляризованных лучей исследовалась в классич. опытах О. Френеля (A. Fresnel) и Д. Ф. Араго (D. F. Arago) (1816). Наиб, контраст интерференц. картины наблюдается при сложении когерентных колебаний одного вида поляризации (линейных, круговых, эллиптич.) с совпадающими азимутами. Интерференция никогда не наблюдается, если волны поляризованы во взаимно перпендикулярных плоскостях. При сложении двух линейно поляризованных взаимно перпендикулярных колебаний в общем случае возникает эллиптически поляризованное колебание, интенсивность к-рого равна сумме интенсивностей исходных колебаний. Интерференцию поляризованных лучей можно наблюдать, напр., при прохождении линейно поляризованного света через анизотропные среды. Проходя через такую среду, поляризованное колебание разделяется на два когерентных элементарных ортогональных колебания, распространяющихся с разл. скоростью. Далее одно из этих колебаний преобразуют в ортогональное (чтобы получить совпадающие азимуты) или выделяют из обоих колебаний составляющие одного вида поляризации с совпадающими азимутами. Схема наблюдения интерференции поляризованных лучей в параллельных лучах дана на рис. 1, а. Пучок параллельных лучей выходит из поляризатора N1 линейно поляризованным в направлении N1N1 (рис. 1, б). В пластинке К, вырезанной из двоякопреломляющего одноосного кристалла параллельно его оптич. оси ОО и расположенной перпендикулярно падающим лучам, происходит разделение колебания N1N1 на составляющие Ае, параллельную оптич. оси (необыкновенную), и A0, перпендикулярную оптич. оси (обыкновенную). Для повышения контраста интерференц. картины угол между N1N1 и А0 устанавливают равным 45°, благодаря чему амплитуды колебаний Ае и А0 равны. Показатели преломления nе и n0 для этих двух лучей различны, а следовательно, различны и скорости их распространения в К, вследствие чего на выходе пластины К между ними возникает разность фаз d=(2p/l)(n0-nе), где l - толщина пластинки, l - длина волны падающего света.
|
Рис. 1. Наблюдение интерференции поляризованных лучей в параллельных лучах: |
Анализатор N2 из каждого луча Ае и А0 пропускает только составляющие с колебаниями, параллельными его направлению пропускания N2N2. Если гл. сечения поляризатора и анализатора скрещены (N1^N2), то амплитуды слагающих А1 и А2 равны, а разность фаз между ними D=d+p. Т. к. эти составляющие когерентны и линейно поляризованы в одном направлении, то они интерферируют. В зависимости от величины D на к--л. участке пластинки наблюдатель видит этот участок тёмным [d=(2k+1)pl, k - целое число] или светлым (d=2kpl) в монохроматич. свете и различно окрашенным в белом свете (т.н. хроматич. поляризация). Если пластинка неоднородна по толщине пли по показателю преломления, то места её с одинаковыми этими параметрами будут соответственно одинаково тёмными или одинаково светлыми (или одинаково окрашенными в белом свете). Кривые одинаковой цветности наз. изохромами. Пример схемы наблюдения интерференции поляризованных лучей в сходящихся лунах показан на рис. 2. Сходящийся плоскополяризованный пучок лучей из линзы L1 падает на пластинку, вырезанную из одноосного кристалла перпендикулярно его оптич. оси. При этом лучи разного наклона проходят разные пути в пластинке, а обыкновенный и необыкновенный лучи приобретают разность хода D=(2pl/lcosy)(n0-nе), где y - угол между направлением распространения лучей и нормалью к поверхности кристалла. Наблюдаемая в этом случае интерференц. картина дана на рис. 1, а к ст. Коноскопические фигуры. Точки, соответствующие одинаковым разностям фаз D,
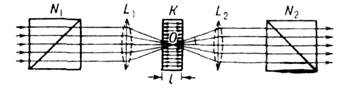
Рис. 2. Схема для наблюдения интерференции поляризованных лучей в сходящихся лучах: N1, - поляризатор; N2, - анализатор, К - пластинка толщиной l, вырезанная из одноосного двупреломляющего кристалла; L1, L2 - линзы.
расположены по концентрич. окружности (тёмным или светлым в зависимости от D). Лучи, входящие в К с колебаниями, параллельными гл. плоскости или перпендикулярными ей, не разделяются на два слагающих и при N2^N1 не будут пропущены анализатором N2. В этих плоскостях получится тёмный крест. Если N2||N1, крест будет светлым. Интерференция поляризованных лучей применяется в кристаллооптике, минералогии и петрографии для диагностики минералов и горных пород, для определения ориентации кристаллов и изучения их дефектов. На использовании интерференции поляризованных лучей основан ряд различных по устройству и назначению поляризационных приборов: поляриметры для исследования механич. напряжений в деталях машин и сооружений (поляризационно-оптический метод исследования напряжений); интерференционно-поляризац. фильтры с шириной полосы в сотые доли нм, используемые для гелиофиз. исследований и в практике физ. эксперимента; компенсаторы, фазовые модуляторы.

|
|