К сожалению, в течение ХХ века, когда реальная физика была попрана захватившими ее паразитарными общественными силами, превративших физику в предмет и инструмент манипулирования сознанием и общественным положением людей, понятие физическое электрической емкости было превращено в некий схоластический абсурд. В частности, в системе СГСЭ, нарушающей физические размерности, электрическая ёмкость уединённого проводящего шара в вакууме равна его радиусу r [cm]. На самом деле электрическая емкость не имеет размерности длины, а отражает физическую ёмкость проводящего тела по отношению к электрическому заряду, что непосредственно отражается в самой размерности [C/V], то есть то, насколько увеличится заряд [C] проводящего тела при изменении его электрического потенциала на 1V.
Исходя из последнего, электрическая ёмкость шара, расположенного в однородной изотропной среде с абсолютной диэлектрической проницаемостью εa, равна
С = 4πεаr [F].
В математико-теоретическом, упрощенном случае электрическая ёмкость геометрически подобных проводящих тел пропорциональна их линейным размерам, то есть для ёмкостей "лабораторных" масштабов - масштабов мезофизики (примерно от миллиметра до километра) имеет место свойство автомодельности. В микромире и мегамире - масштабах, существенно отличных от мезомира линейный характер зависимости емкости от размеров нарушается.
Традиционно, то есть с позитивистски-релятивистских позиций, электрические емкости делят на уединённые и сложные (системные).
Таким образом уединённую ёмкость не считают конденсатором, а её свойства считаются простыми.
Реально дело обстоит иначе. Уединённая ёмкость в отличие от составной создает в окружающем пространстве (Эфире) электрическое поле весьма сложного, часто непредсказуемого математической моделью поведения при любых изменениях внешних по отношению к этой ёмкости факторов. Примерами могут служить излучение электромагнитных волн, облучение (приём) электромагнитных волн, обмен энергией, импульсом и моментом с внешним полем, к примеру, в результате движения внешних тел или самой ёмкости в Эфире (относительно "лабораторной" системы). Кроме того, уединённой ёмкость является только в теории. Реально - это конденсатор, имеющий удаленные друг от друга обкладки. Второй часто является поверхность Земли, имеющая нулевой потенциал и неявно для теоретика, но физически реально соединённая с вторым выводом источника э.д.с., создающего потенциал на уединённой ёмкости. Отключение источника э.д.с. по завершении процесса зарядки ёмкости не говорит об отсутствии двухполюсности, но лишь об отключении ее после завершения процесса, то есть временном отсутствии тока. Уже по своему определению уединённая ёмкость - это тоже конденсатор, накапливающий заряд.
Бо́льшая часть электрического поля составной ёмкости состедоточена внутри нее самой. Таким образом поведение этого поля предсказуемо и просто. Оно определяется геометрической конфигурацией ёмкости. Составная ёмкость может играть роль уединённой без каких-либо конструктивных изменений, - достаточно только, чтобы заряжающий и разряжающий ёмкость источник создавал на ее обкладках одинаковый потенциал. Последнее показывает, что форма, конструкция проводников ёмкости сама по себе не определяет тип ёмкости - уединенная или составная.
Таким образом традиционная классификация емкостей является фукнционально неопределённой. Поэтому видится видится целесообразным дополнительное введение функциональной классификации емкостей.
Традиционно, электрическую ёмкость рассматривают и рассчитывают, как атрибут электростатики. Однако это не соответствует физическим реалиям, ограничивая видение физического явления электрической ёмкости узкой областью электростатики. Реально, явление электрической ёмкости возникает как в электростатике, так и в электродинамике. Поэтому, существуют две ее разновидности:
Существует два вида электрических емкостей, превосходящих по плотности заряда и, соответственно, своей ёмкости остальные.
Есть еще пара разновидностей характеристик ёмкости.
В СИ единицей измерения ёмкости является фарада [F]. В мезофизической системе n проводящих тел связь зарядов тел с их потенциалами линейная (см., напр., [1-3]) и описывается тремя способами:
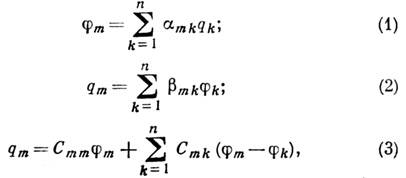
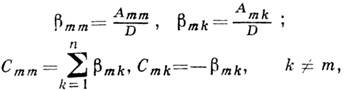
В электротехнике обычно пользуются коэффициентом Сmm и Cmk. Частичная собственная ёмкость Cmm = qm/φm при равенстве потенциалов всех тел, а частичная взаимная ёмкость Cmk = Ckm = -qm/φk при нулевых потенциалах всех тел, кроме потенциала тела k.
В практически интересном случае двух проводящих тел их электрическая емкость численно равна заряду q, который нужно перенести с одного тела на другое, с тем чтобы изменить разность потенциалов φ1 - φ2 на единицу, и определяется соотношением С = q/(φ1-φ2). Из (3) следует, что в этом случае
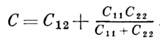
Как правило, частичная взаимная электрическая емкость C12 двух тел, расположенных на расстояниях, соизмеримых с их размерами, значительно больше частичных собственных электрических емкостей C11 и С22. Электрическая емкость двух близко расположенных проводящих пластин без учёта влияния краевых эффектов (в СИ):
С =εaS/d,
где d - расстояние между пластинами, S - площадь пластины.
Электрическая емкость двух сферических проводящих поверхностей с общим центром:
С=4πεаr1r2/(r1-r2),
где r1 и r2 - радиусы внутр. и внеш. поверхностей. Электрическая емкость двух соосных цилиндрич. проводящих поверхностей без учёта эффектов на концах цилиндров:
С= 2πεаl//ln(r2/r1),
где r1 и r2 - радиусы поверхностей, l - длина цилиндров.
Электрическая емкость двухпроводной линии:
C = pεаl/ln(d/a-1),
где a - радиус проводов, d - расстояние между осями проводов, l - длина линии.
Электрическая емкость провода воздушной трёхфазной линии, расположенной над Землёй:
C = 2πεаl/ln[2hd/(aD)],
где l - длина линии, h - среднее геометрическое значение высоты проводов над землёй, d - среднее геометрическое значение расстояний между проводами, D - ср. геом. значение расстояний между проводами и зеркальными (относительно Земли) изображениями соседних проводов.
В технике для получения нужных величин электрической емкости используются специальные устройства - конденсаторы. Все другие элементы и устройства, применяемые в электрических цепях различного назначения, также обладают электрической емкостью. Так, например, трансформаторы имеют межвитковую ёмкость, ёмкость между выводами, ёмкость между обмотками и тому подобное, все электронные приборы - межэлектродные ёмкости, протяжённые устройства обладают распределённой по длине электрической емкости и т. д. Влияние этих ёмкостей в некоторых режимах может быть существенным.
В теории электрических цепей электрическая емкость - параметр ёмкостного элемента электрической схемы, представляющего собой двухполюсник, характеризующийся зависимостью заряда от напряжения q(U), которая может быть линейной (в случае линейной ёмкости) или нелинейной (в случае нелинейной ёмкости; см., например, Варикап ).
Действующие значения синусоидальных токов I и напряжения в линейной ёмкости связаны соотношением:
U=xcI,
где xс=(ωС)-1 - ёмкостное сопротивление, ω - круговая частота синусоидальных токов и напряжения.
В нелинейных ёмкостях синусоидальное напряжение вызывает несинусоидальный ток. Электрическая емкость как элемент схемы соответствует элементу цепи - конденсатору при его идеализации.
В металлах имеются свободные носители электричества – электроны проводимости (электронный газ), которые под действием внешнего электрического поля могут перемещаться в пределах всего объема металла. Под действием внешнего электрического поля электроны в металле перераспределяются таким образом, чтобы в любой точке внутри проводника электрическое поле электронов проводимости и положительно заряженных "атомных остатков" полностью скомпенсировало внешнее поле. В этом случае имеет место
Возникающие при этом на поверхности заряды называются индуцированными зарядами, которые исчезают, как только металл удаляется из электрического поля. Вектор напряженности внешнего поля у поверхности металла направлен по нормали к поверхности, так как касательная составляющая вектора вызывала бы перемещение носителей тока по поверхности. Таким образом:
так как во всех точках поверхности S, проходящей внутри металла, Е=0.
где Dn и Еn – проекции векторов D и Е на внешнюю нормаль к поверхности металла, ε – диэлектрическая проницаемость среды.
Уединённым проводником называется металлическое тело, находящееся столь далеко от других металлических тел и заряженных объектов, что влиянием их электрических полей можно пренебречь.
Значение 
больше там, где меньше радиус кривизны поверхности.
где r – расстояние от заряда σdS малого элемента поверхности до какой-либо точки на этой поверхности. Интеграл зависит только от размеров и формы проводника.
где величина С называется электрической емкостью проводника
Электрическая емкость уединённого проводника зависит от его размеров и формы, а также от диэлектрических свойств окружающей среды. Электрическая емкость уединённого проводника не зависит от материала проводника и его агрегатного состояния, а также от формы и размеров полостей внутри проводника..
Электрическая емкость проводника становится больше, если вблизи есть другие проводники. Для двух близко расположенных проводников взаимная емкость равна
Взаимная емкость двух проводников зависит от их формы, размеров и взаимного расположения, а также от диэлектрических свойств окружающей среды.
Система из двух проводников, равномерно заряженных равными по величине и противоположными по знаку зарядами, называется конденсатором, если создаваемое ими поле локализовано в ограниченной области пространства. Емкость плоского конденсатора из двух пластин с площадью S каждая, расположенных на расстоянии d друг от друга, равна
(справедливо при 
)
Емкость сферического конденсатора
Емкость цилиндрического конденсатора
Пробивное напряжение (напряжение пробоя) – минимальная разность потенциалов обкладок конденсатора, при которой происходит электрический разряд через слой диэлектрика. Зависит от формы и размеров обкладок и от свойств диэлектрика. При последовательном соединении конденсаторов емкость батареи
При параллельном соединении конденсаторов емкость батареи
Работа против кулоновских сил при заряде проводника идет на увеличении электрической энергии проводника, которая аналогична механической потенциальной энергии. Работа dA по перенесению заряда dq из бесконечности на уединённый проводник определяет величину электрической энергии (потенциальной) этого проводника
→ 
Энергия заряженного конденсатора
Энергия любой системы неподвижных зарядов
Энергия однородного поля плоского конденсатора
Объемная плотность энергии однородного поля
Объемная плотность энергии неоднородного поля
→ 
→ 
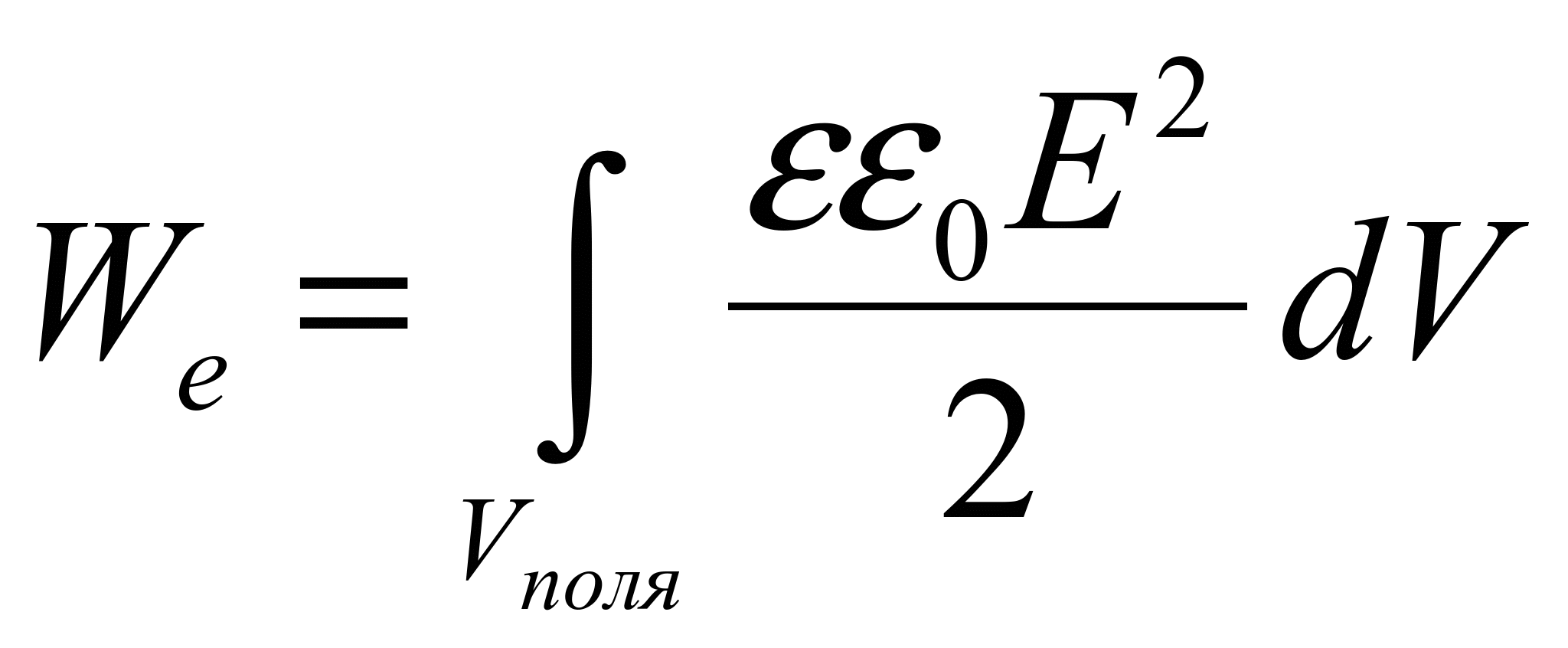
Пример: Энергия и объемная плотность энергии поля заряженной сферы
Действующие в электрическом поле силы могут совершать работу по перемещению заряженных тел. Такие силы называются пондемоторные силы.
Пример: сила притяжения пластин конденсатора может быть определена из предположения, что действующая сила, уменьшая расстояние между пластинами, уменьшает потенциальную энергию системы
Из выражения для энергии поля и емкости конденсатора следует
и 
→ 
Тогда сила действующая на пластины
будет силой притяжения.
Энергия электрического поля системы заряженных тел изменяется, если тела системы перемещаются и/или изменяются их заряды. При этом совершается работа внешними силами и источниками электрической энергии. Для малого изменения состояния системы (свойства системы не изменяются)
(закон сохранения энергии)
где 
- работа внешних сил, 
- работа источников электрической энергии, 
- изменение энергии электрического поля системы, 
- изменение кинетической энергии системы, 
- теплота, выделяющаяся при изменении или перераспределении заряда системы.
Если перемещение заряженных тел происходит медленно (квазистатически), то можно пренебречь кинетической энергией и считать, что работа внешних сил численно равна и противоположна по знаку работе пондемоторных сил 
. Тогда
Если заряд системы не изменяется, то
и 
→ 
работа пондемоторных сил равна убыли энергии электрического поля системы.
К.А. Хайдаров
|
|
 |
