Рассеяние волн на случайной поверхности - рассеяние волн на статистически неровной
границе раздела двух сред. Рассеяние волн на случайной поверхности оказывает существ. влияние на характер
распространения радиоволн в естеств. условиях: рассеяние на неровностях рельефа
земной поверхности, взволнованной поверхности моря, ниж. границе ионосферы приводит
к флуктуациям параметров радиосигналов. При передаче сигналов по вол-новодным
или квазиоптич. линиям передачи шероховатость поверхности является причиной
появления паразитных мод, искажения передаваемых сигналов и их дополнит. затухания.
При работе радиолокац. и радиометрич. систем Р. в. на с. п., с одной стороны,
является источником пассивных помех, маскирующих полезный сигнал, а с другой
- содержит полезную информацию о параметрах рассеивающей поверхности, являясь
физ. основой методов дистанц. зондирования окружающей среды, напр. для определения
по радиолокац. (радиометрич.) данным параметров морского волнения, состояния
ледового и снежного покрова, степени расчленённости рельефа и т. д. В задачах
гидро- и сейсмоакустики аналогичную роль играет рассеяние звука на поверхности
и дне океана, на др. границах раздела сред с различающимися физ. параметрами.
В оптике Р. в. на с. п. приводит к нарушению законов зеркального отражения и
преломления, является причиной искажений изображения в реальных оптич. системах
и диффузного рассеяния света разл. матовыми поверхностями. В физике твёрдого
тела рассеяние разл. квазичастиц, трактуемых как волны, на естеств. шероховатой
поверхности образца приводит к уменьшению времени их жизни, затуханию собств.
состояний (напр., магн. поверхностных уровней), влияет на характер скин-эффекта
и др. кинетич. явлений (электро- и теплопроводность тонких плёнок, расширение
линий резонансных переходов между разл. квантовыми состояниями и т. д.).

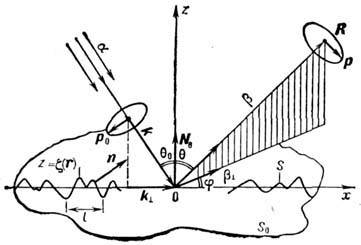
Отклонения неровной поверхности S (рис.)
от ср. плоскости г = 0 описываются случайной функцией z = = x(r),
где r = (х, у), усреднение по ансамблю реализаций этой
функции обозначается <...>. Скалярное волновое поле U(R, t), R
= (r, z) (либо любая компонента векторного) в результате
Р. в. на с. п. также становится случайным и может быть представлено в виде суммы
среднего (когерентного) поля <U> и флуктуаци-онного (некогерентного)
поля и. Для описания Р. в. на с. п. в качестве первичного поля достаточно,
в силу принципа суперпозиции, рассмотреть плоскую монохроматич. волну Ui
= exp[i(kR - wt)] с волновым вектором k
и частотой w, падающую из верх. полупространства под углом q0
на границу раздела двух сред. Ниже описываются только отражённые волны, рассеянные
в верх. полупространство. Для решения задачи о Р. в. на с. п. используют след.
приближённые методы.
Метод малых возмущений (ММВ) применяют
для достаточно низких и пологих неровностей:
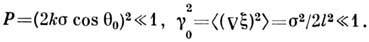
Здесь P - параметр Рэлея, 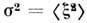 - дисперсия высот неровностей, l -
их радиус корреляции,
- дисперсия высот неровностей, l -
их радиус корреляции,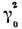 -
дисперсия наклонов. При скользящем распространении (q0 :
p/2) вместо P следует требовать малости параметра Фейнберга:
-
дисперсия наклонов. При скользящем распространении (q0 :
p/2) вместо P следует требовать малости параметра Фейнберга: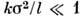 Рассеянное волновое поле U представляют в виде ряда U = U0
+ u1 + u2 + ···, где U0 - отражённое (преломлённое) поле на плоской границе (x = 0), а ип
~ ~ xn - малые поправки к U0. Если
ограничиться только первыми двумя слагаемыми в ряде ММВ, то ср. поле
Рассеянное волновое поле U представляют в виде ряда U = U0
+ u1 + u2 + ···, где U0 - отражённое (преломлённое) поле на плоской границе (x = 0), а ип
~ ~ xn - малые поправки к U0. Если
ограничиться только первыми двумя слагаемыми в ряде ММВ, то ср. поле 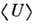 совпадает с невозмущённым U0, а флуктуац. поле и -
с однократно рассеянным полем и1 (борновское приближение).
совпадает с невозмущённым U0, а флуктуац. поле и -
с однократно рассеянным полем и1 (борновское приближение).
Рассеивающие свойства неровной поверхности характеризуют
уд. эфф. поверхностью рассеяния 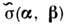 ,
к-рая определяется как умноженное на 4p отношение ср. потока энергии флуктуац.
поля и, рассеянного с единицы площади S0 в
единичный телесный угол в направлении b, к плотности потока энергии
в падающей волне, распространяющейся в направлении a = k/k:
,
к-рая определяется как умноженное на 4p отношение ср. потока энергии флуктуац.
поля и, рассеянного с единицы площади S0 в
единичный телесный угол в направлении b, к плотности потока энергии
в падающей волне, распространяющейся в направлении a = k/k:
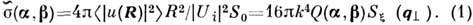
Здесь R - расстояние от центра рассеивающей
площадки S0 до точки наблюдения R, находящейся
в дальней зоне (зоне Фраунгофера); q = = k(b-a)
- вектор рассеяния, 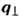 - его проекция на плоскость z = 0,
Sx(q)- пространств. спектральная плотность неровностей,
связанная преобразованием Фурье с их корреляционной функцией
- его проекция на плоскость z = 0,
Sx(q)- пространств. спектральная плотность неровностей,
связанная преобразованием Фурье с их корреляционной функцией 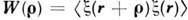 , для пространственно однородной статистически неровной поверхности
, для пространственно однородной статистически неровной поверхности
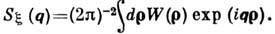
Явный вид не зависящего от параметров неровностей
множителя Q(a, b) определяется конкретными условиями.
Напр., при рассеянии звука на абсолютно мягкой поверхности (U|S
= 0)
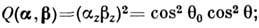
на абсолютно жёсткой поверхности (9Ul9n|S
= 0)
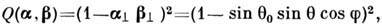
здесь f - угол между плоскостью падения
(a, N0) и плоскостью рассеяния (b,
N0), N0 -
орт вдоль оси Оz. При рассеянии эл--магн. волны на идеально проводящей
поверхности
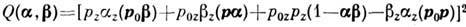 ,
,
где p0, p
- единичные векторы поляризации падающей волны и приёмника, ортогональные
к направлениям распространения волн: (р0a)
= (рb) = 0. При обратном рассеянии b = -a
(в радиолокации) на неровной границе раздела двух сред с диэлектрич. проницаемостя-ми
e1 = 1 и e2 = e:
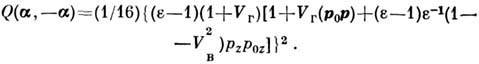
Здесь Vг,в(q0) - коэф.
отражения Френеля для горизонтальной (Г) и вертикальной (В) поляризации (см.
Френеля формулы).
Р. в. на с. п. в борновском приближении, как
следует из ф-лы (1), является резонансным: из направления a в
направление b рассеивает только одна пространств. гармоника из спектра
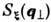 неровностей
поверхности, волновой вектор к-рой совпадает с проекцией вектора рассеяния q
на плоскость z = 0.
неровностей
поверхности, волновой вектор к-рой совпадает с проекцией вектора рассеяния q
на плоскость z = 0.
Модифицированная теория возмущений (МТВ) учитывает
при расчёте ср. поля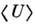 многократное
рассеяние. Отражение ср. поля
многократное
рассеяние. Отражение ср. поля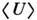 от
случайной поверхности происходит так же, как и от плоской границы раздела z
= 0, но с эфф. поверхностным импедансом
от
случайной поверхности происходит так же, как и от плоской границы раздела z
= 0, но с эфф. поверхностным импедансом 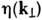 , зависящим от длины волны l и направления облучения, т. е. при Р. в.
на с. п. имеет место дисперсия пространственная .Для абсолютно жёсткой
поверхности
, зависящим от длины волны l и направления облучения, т. е. при Р. в.
на с. п. имеет место дисперсия пространственная .Для абсолютно жёсткой
поверхности 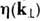 выражается через интеграл по всем направлениям рассеяния b от величины
выражается через интеграл по всем направлениям рассеяния b от величины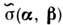 ,
аналитически продолженной
,
аналитически продолженной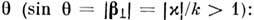 в
область комплексных углов рассеяния
в
область комплексных углов рассеяния
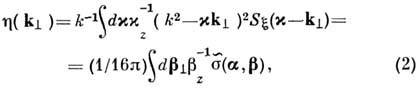
где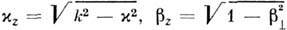
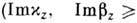
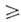 0). Активная часть импеданса
0). Активная часть импеданса 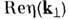 пропорциональна энергии, рассеянной во флуктуац.
поле, и определяется интегралом (2) только по вещественным углам рассеяния
пропорциональна энергии, рассеянной во флуктуац.
поле, и определяется интегралом (2) только по вещественным углам рассеяния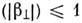 ,
рассеяние происходит в однородные уходящие
от поверхности волны; реактивная часть
,
рассеяние происходит в однородные уходящие
от поверхности волны; реактивная часть 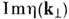 связана с рассеянием в неоднородные волны
связана с рассеянием в неоднородные волны 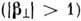 , ею обусловлены сдвиг фаз между падающей и отражённой волнами и замедление
поверхностных волн, распространяющихся над шероховатой жёсткой поверхностью.
, ею обусловлены сдвиг фаз между падающей и отражённой волнами и замедление
поверхностных волн, распространяющихся над шероховатой жёсткой поверхностью.
При рассеянии эл--магн. волн статистически неровная
поверхность по отношению к когерентному полю эквивалентна импедансной, вообще
говоря, анизотропной плоскости, описываемой тензором поверхностного импенданса
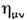 : m, v
= x, у, связывающего тангенц. компоненты ср. электрич. E
и магн. H полей:
: m, v
= x, у, связывающего тангенц. компоненты ср. электрич. E
и магн. H полей:
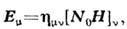
для идеально проводящей поверхности (|e|:,)
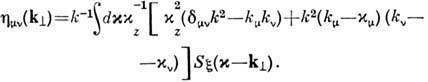
При рассеянии волн на изменяющейся во времени
границе раздела, возмущения к-рой можно представить в виде суперпозиции бегущих
плоских волн с волновыми векторами p и частотами W(p),
происходит изменение частоты рассеянных волн по сравнению с частотой падающей
волны w. В борновском приближении спектр рассеянного поля в зоне Фраунгофера
состоит из двух комбинац. частот:
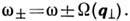
Затухание поверхностных волн [ImW(p).0],
а также след. порядки в ММВ отражаются в расширении спектра рассеянного поля
и появлении др. комбинац. частот.
В ближней зоне (зоне Френеля) интерференция рассеянных
волн приводит к флуктуациям амплитуды и фазы волнового поля, характер к-рых
определяется значением волнового параметра D = R/kl2cosq0, равного по порядку величины ср. числу неровностей в первой зоне Френеля:
при D 1
- флуктуации амплитуды малы, а дисперсия флуктуации фазы равна параметру Рэлея
Р; при D
1
- флуктуации амплитуды малы, а дисперсия флуктуации фазы равна параметру Рэлея
Р; при D  1 - флуктуации амплитуды и фазы некоррелиро-ваны,
а их дисперсии совпадают и равны Р/2.
1 - флуктуации амплитуды и фазы некоррелиро-ваны,
а их дисперсии совпадают и равны Р/2.
Метод касательной плоскости (МКП), или
метод Кирхгофа, применяют для решения задач о Р. в. на с. п. с большими по сравнению
с l неровностями. При этом допустимы сколь угодно большие значения параметра
Рэлея, однако неровности должны быть достаточно гладкими -kacos3q'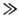 1,
где а - характерный радиус кривизны поверхности, а q' - локальный
угол падения, соsq' = -(па). В основе МКП лежит предположение
о том, что поле U в каждой точке RS поверхности S можно представить в виде суммы полей падающей волны и волны, зеркально отражённой
от плоскости, касательной к поверхности в точке Rs; поле
в произвольной точке R затем определяют по Грина формуле в
соответствии с принципом Гюйгенса - Френеля. После усреднения по ансамблю реализаций
x(r)когерентное поле <U> распространяется только
в направлении зеркального отражения от ср. плоскости z = 0, отличаясь
от поля нулевого приближения U0 на эфф. коэф. отражения VЭ:
1,
где а - характерный радиус кривизны поверхности, а q' - локальный
угол падения, соsq' = -(па). В основе МКП лежит предположение
о том, что поле U в каждой точке RS поверхности S можно представить в виде суммы полей падающей волны и волны, зеркально отражённой
от плоскости, касательной к поверхности в точке Rs; поле
в произвольной точке R затем определяют по Грина формуле в
соответствии с принципом Гюйгенса - Френеля. После усреднения по ансамблю реализаций
x(r)когерентное поле <U> распространяется только
в направлении зеркального отражения от ср. плоскости z = 0, отличаясь
от поля нулевого приближения U0 на эфф. коэф. отражения VЭ:
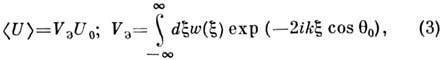
w(x) - плотность распределения
вероятности случайных отклонений x от ср. плоскости z = 0. Для нормальной
случайной поверхности, отклонения к-рой от ср. плоскости соответствуют Гаусса
распределению, VЭ = exp (- P/2).
Некогерентное рассеяние в заданном направлении
при больших значениях параметра Рэлея определяется вероятностью зеркально отражающих
из a в b наклонов поверхности g3 = -q^/qz
(с нормалью n3 = q/q):
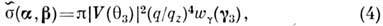
где wg - плотность
распределения вероятностей наклонов g =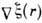 ,
a V(q3) - коэф. отражения Френеля при зеркальных углах
падения, cosq3 = (n3b)
= - (n3a).
,
a V(q3) - коэф. отражения Френеля при зеркальных углах
падения, cosq3 = (n3b)
= - (n3a).
Учёт затенений поверхности в рамках МКП сводится
к тому, что в ф-лах (3) и (4) под функциями w(x) и wg
следует понимать плотности распределения высот и наклонов
только освещённых (но отношению к направлениям a и b) участков поверхности.
Величина 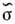 в
форме (4) не зависит от длины волны излучения и по сути является следствием
применения геометрической оптики метода .Расчёт дифракц. эффектов приводит
к поправкам к МКП ~ s2/k2l4,
а для эл--магн. волн в радио-локац. случае (b = -a) - к появлению
деполяризации рассеянного поля, что не удаётся выявить в рамках ММВ и МКП.
в
форме (4) не зависит от длины волны излучения и по сути является следствием
применения геометрической оптики метода .Расчёт дифракц. эффектов приводит
к поправкам к МКП ~ s2/k2l4,
а для эл--магн. волн в радио-локац. случае (b = -a) - к появлению
деполяризации рассеянного поля, что не удаётся выявить в рамках ММВ и МКП.
Двухмасштабную модель (ДММ) применяют
для интерпретации эксперим. данных по Р. в. на с. п. с широким спектром вертикальных
и горизонтальных масштабов неровностей, когда не выполняются условия применимости
ни ММВ, ни МКП. Шероховатую поверхность в ДММ рассматривают как суперпозицию
мелкомасштабной "ряби" (для расчёта рассеяния на к-рой применим
ММВ) и гладких крупномасштабных неровностей z = Z(r)с наклонами
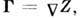 удовлетворяющими
МКП. В результате
удовлетворяющими
МКП. В результате 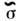 представляется в виде суммы (4) (где следует заменить g на Г) и
усреднённой по наклонам крупномасштабной поверхности Г величины
представляется в виде суммы (4) (где следует заменить g на Г) и
усреднённой по наклонам крупномасштабной поверхности Г величины 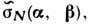 рассчитанной по ф-ле (1) для шероховатой плоскости со ср. нормалью N
= (N0 - Г)(1 + Г2)-1/2:
рассчитанной по ф-ле (1) для шероховатой плоскости со ср. нормалью N
= (N0 - Г)(1 + Г2)-1/2:
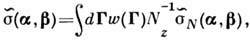
где w(Г) - плотность распределения
вероятностей наклонов Г. С помощью ДММ описывают рассеяние радиоволн взволнованной
морской поверхностью и поверхностью Луны, рассеяние звука поверхностью и дном
океана.
Метод малых наклонов (ММН) применяют для
расчёта Р. в. на с. п. с неровностями произвольной высоты, но достаточно пологими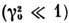 .
Для низких неровностей ММН приводит к ф-лам
ММВ, для высоких - к МКП. Первый член ряда по g0 получается
из ф-лы (1) борновского приближения для
.
Для низких неровностей ММН приводит к ф-лам
ММВ, для высоких - к МКП. Первый член ряда по g0 получается
из ф-лы (1) борновского приближения для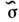 (определённого для полного рассеянного поля, а не только флуктуационного) заменой:
(определённого для полного рассеянного поля, а не только флуктуационного) заменой:
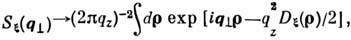
где Dx (r) = < [x(r+r) - x(r)]2 > - структурная функция неровностей нормальной (гауссовой) поверхности. Учёт когерентности волн, испытывающих многократные рассеяния на сильношероховатой поверхности и распространяющихся в противоположных направлениях по одним и тем же траекториям, приводит к явлению усиления обратного рассеяния, аналогичного тому, к-рое имеет место при рассеянии волн на объёмных неод-нородностях. См. также Дифракция волн, Рассеяние звука, Рассеяние света.

И. М. Фукс
|
|