Френеля формулы - определяют отношения амплитуды, фазы и состояния поляризации отражённой и преломлённой
световых волн, возникающих при прохождении света через границу раздела двух
прозрачных диэлектриков, к соответствующим характеристикам падающей волны. Установлены
О. Ж. Френелем в 1823 на основе представлений об упругих поперечных колебаниях
эфира. Однако те же самые соотношения - Ф. ф.- следуют в результате строгого
вывода из эл--магн. теории света при решении ур-ний Максвелла.
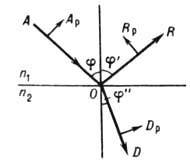
Пусть плоская световая
волна падает на границу раздела двух сред с показателями преломления п1
и п2 (рис.). Углы j, j' и j'' есть соответственно
углы падения, отражения и преломления, причём всегда n1
sinj=n2sinj'' (закон преломления)
и |j|=|j'| (закон отражения). Амплитуду электрического
вектора падающей волны А разложим на составляющую
с амплитудой Ар, параллельную плоскости падения, и
составляющую с амплитудой As, перпендикулярную плоскости
падения. Аналогично разложим амплиту ды отражённой волны R на составляющие
Rp и Rs, а преломлённой волны D - на
Dp и Ds (на рис. показаны только р-составляющие).
Ф. ф. для этих амплитуд имеют вид
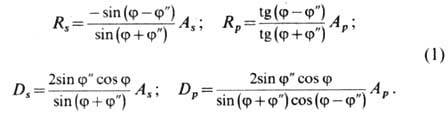
Из (1) следует, что при
любом значении углов j и j'' знаки Ар и Dp совпадают. Это означает, что совпадают и фазы, т. е. во всех случаях преломлённая
волна сохраняет фазу падающей. Для компонент отражённой волны (Rp и Rs)фазовые соотношения зависят от j, n1
и n2; если j=0, то при n2>n1
фаза отражённой волны сдвигается на p.
В экспериментах обычно
измеряют не амплитуду световой волны, а её интенсивность, т. е. переносимый
ею поток энергии, пропорциональный квадрату амплитуды (см.
Пойнтинга вектор ).Отношения
средних за период потоков энергии в отражённой и преломлённой волнах к среднему
потоку энергии в падающей волне наз. коэф. отражения r и коэф. прохождения
d. Из (1) получим Ф. ф., определяющие коэф. отражения и преломления для
s- и р-составля-ющих падающей волны, учтя, что
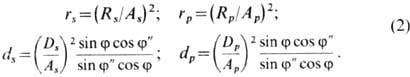
В отсутствие поглощения
света между коэффициентами в соответствии с законами сохранения энергии
существуют отношения rs+ds=1 и rp+dp=1.
Если на границу раздела падает естественный свет ,т. е. все направления
колебаний электрич. вектора равновероятны, то энергия волны поровну делится
между р- и s-колебаниями, полный коэф. отражения в этом случае
r=(1/2)(rs+rp) Если j+j''=90o,
то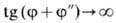 
и
rp=0 т. е. в этих условиях свет, поляризованный так, что его
электрич. вектор лежит в плоскости падения, совсем не отражается от поверхности
раздела. При падении естеств. света под таким углом отражённый свет будет полностью
поляризован. Угол падения, при к-ром это происходит, наз. углом полной поляризации
или у г л о м Б р ю с т е р а (см. Брюстера закон ),для него справедливо
соотношение lgjБ=n2/n1.
При нормальном падении
света на границу раздела двух сред (j = 0) Ф. ф. для амплитуд отражённой и преломлённой
волн могут быть приведены к виду
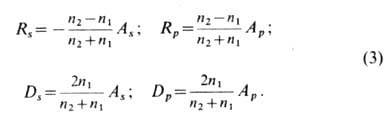
Здесь исчезает различие
между составляющими s и p, т. к. понятие плоскости падения теряет
смысл. В этом случае, в частности, получаем
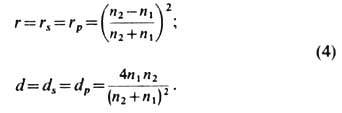
Из (4) следует, что отражение
света на границе раздела тем больше, чем больше абс. величина разности n2
- n1; коэф. r и d не зависят от того, с
какой стороны границы раздела приходит падающая световая волна.
Условие применимости Ф. ф.- независимость показателя преломления среды от амплитуды вектора электрич. напряжённости световой волны. Это условие, тривиальное в классич. (линейной) оптике, не выполняется для световых потоков большой мощности, напр. излучаемых лазерами. В таких случаях Ф. ф. не дают удовлетворит. описания наблюдаемых явлений и необходимо использовать методы и понятия нелинейной оптики.
|
|
 |
