Парадоксы кинетической теории, газов возникли в связи с попытками обоснования второго начала термодинамики исходя из ур-ний механики. Обратимость ур-ний механики по отношению к обращению времени (замене t - > - t)связана с тем, что (в отсутствие магн. поля) они содержат лишь вторые производные по времени, и поэтому нельзя отличить ур-ния механики, написанные для возрастающего времени, от ур-ний для убывающего времени. Если Н-функцию Больцмана можно было бы получить лишь на основе механики, это привело бы к противоречию со вторым началом термодинамики о возрастании энтропии, т. к. для газов энтропия равна Н-функции Больцмана (умноженной на k) с обратным знаком.
При формулировке П. о. предполагается, что кинетич. ур-ние можно вывести из ур-ний механики без привлечения к--л. вероятностных гипотез. В действительности в выводе Больцмана неявно содержится предположение вероятностного характера о том, что число столкновений пропорц. произведению функций распределения сталкивающихся частиц, т. е. состояния между каждым столкновением не коррелируют (гипотеза "молекулярного хаоса"). Более строгий выво;(, кинетич. ур-ния, данный Н. Н. Боголюбовым в 1946 [3], явпо использует граничное условие "ослабления корреляции", имеющее вероятностный смысл.
Кроме того, для разъяснения П. о. существенно, что при учёте флуктуации (даже для газа) нет простой связи между энтропией S и одночастичной функцией распределения f1, к-рая следует из ур-ния Больцмана (S = - k (lnf1)). На самом деле это лишь первый член разложения S по степеням плотности. Энтропия может зависеть от флуктуации, к-рые описываются корреляционными функциями. Корреляц. часть энтропии установлена Г. Грином в 1953 [4].
П. о. существенно проясняется теорией флуктуации, т. к. она показывает, что равновесное состояние соответствует максимуму вероятности, а отклонения от него, связанные с заметными флуктуациями, маловероятны. Относит. флуктуация наблюдаемых физ. величин (пропорциональных числу частиц N)имеет порядок
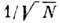(вдали от точек фазового перехода).
Связь явлений необратимости с флуктуациями рассмотрел М. Смолуховский в 1906 - 16 [5] на примерах броуновского движения частиц под действием сил и диффузии в коллоидных растворах. Он исследовал непрерывный переход от необратимого поведения (движения около положения равновесия, замедленного внутр. трением) к неупорядоченному броуновскому движению. Дли коллоидных растворов он исследовал непрерывный переход от обычной необратимой диффузии концентрации примеси к неупорядоченным, случайным флуктуацням концентрации. Кроме того, он дал оценку времени возврата (см. Парадокс возврата)для макроскопич. состояний, к-рое вполне наблюдаемо (для микроскопич. состояний время возврата чрезвычайно велико и находится далеко за пределами возможных наблюдений). Оценки Смолуховского получили эксперим. подтверждение.
Для конденсиров. сред кинетич. ур-ние, вообще говоря, несправедливо, и система описывается функцией распределения fN всех её частиц по координатам и импульсам, удовлетворяющей Лиувилля уравнению, выражающему закон сохранения вероятности в фазовом пространстве. Однако П. о. имеет место и в этом случае. Он связан с кажущимся противоречием между существованием необратимых процессов и обратимым характером ур-ния Лиувилля: симметрией относительно замены времени t
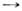- t импульсов частиц pi
- pi при неизменных координатах.
Возможность возрастания энтропии может быть обоснована методами статистич. механики, к-рая приводит к выражению для положительного локального производства энтропии, связанного с внутр. неравновесностью системы, что соответствует термодинамике неравновесных процессов. При этом для кинетических коэффициентов получаются выражения, пропорц. пространственно-временным корреляц. функциям потоков энергии, импульса и вещества (Грина - Кубо формулы ).Энтропия системы в неравновесном случае определяется через локально-равновесное распределение fлок ф-лой
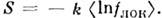Она соответствует максимуму информац. энтропии при условии, что средние
локально-равновесные значения плотности энергии, импульса и числа частиц
равны их средним значениям, причём эти средние вычислены с помощью функции
распределения, удовлетворяющей ур-нию Лиувилля (хотя fлок
ему не удовлетворяет). Возрастание энтропии связано с отбором запаздывающих
решений ур-ния Лиувилля. Опережающие решения должны быть отброшены, т.
к. приводили бы к убыванию энтропии [6]. Отбор запаздывающего решения ур-ния
Лиувилля осуществляется введением в него бесконечно малого члена, нарушающего
его симметрию относительно обращения времени.
