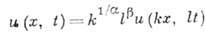,Например, если состояние системы характеризуется
функцией и(х, t), где х - координата, t - время, то условие инвариантности относительно изменения масштабов x'-kx,
t'=lt и преобразования подобия таково:
,
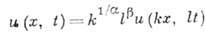где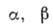 
- числа. Выбор 
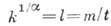, где m - подобия критерий (параметр), придаёт первонач. функции автомодельный вид
.
Т. о., функция и при постоянном т зависит только от комбинации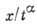 
.
Автомодельность возможна, если набор параметров, определяющих состояние системы, не
содержит характерных масштабов независимых переменных. Поскольку в
большинстве задач форма преобразования подобия заранее неизвестна,
автомодельную подстановку надо в каждом случае находить отдельно. Для
этого имеются 3 способа:
1. Размерностей анализ .Состояние системы характеризуется набором размерных параметров и функций, зависящих от координат х, у, z и времени t. Если один из безразмерных критериев подобия имеет вид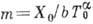 
, где b - параметр, имеющий размерность 
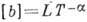, Х0, Т0 - характерные длина и промежуток времени, L, Т - единицы длины и времени соответственно, то в качестве автомодельных переменных можно выбрать безразмерные комбинации 
,
, 
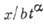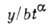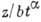. В том случае, когда имеется не более двух определяющих параметров с
независимыми размерностями, отличными от длины и времени, переход к
автомодельным переменным превращает ур-ние с частными производными в
обыкновенное дифференц. ур-ние.
2. Непосредственный подбор. Формально вводится автомодельная замена переменных 
или, в более общем виде,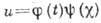 
, 
.
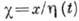Ур-ния, начальные и граничные условия должны иметь структуру,
допускающую такую замену. Решение существует не для любых значений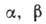 
и не для любых функций 
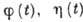. Для получения подходящих значений необходимо решить нелинейную задачу на собств. значения.
3. Исследование групповых свойств ур-ний. Рассмотрим систему дифференц. ур-ний с частными производными 1-го порядка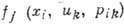 
=0, где 
-независимые переменные,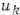 
-искомые функции,
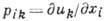Всевозможные замены переменных 
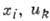, допускаемые системой, образуют группу
Ли. Автомодельные замены являются её однопараметрич. подгруппой
растяжений. В нек-рых случаях найти такие замены позволяет след.
процедура.
В пространстве переменных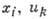 
группа Ли задаётся своими генераторами, имеющими общий вид X=
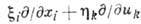, где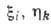
-нек-рые функции переменных х, и; по повторяющимся индексам производится суммирование. В пространстве переменных
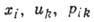группа Ли задаётся генераторами 
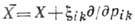, где
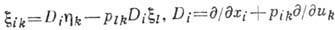. Система ур-ний 
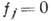определяет гиперповерхность в пространстве переменных 
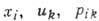, к-рая является инвариантом группы при условии 
,
когда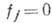 
; эти условия
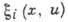служат для определения функций
и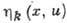
.
Комбинации переменных, дающие искомую
замену, являются первыми интегралами ур-ния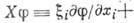
.
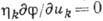Напр., для двух независимых переменных x, t и одной искомой функции
и оператор растяжений имеет
вид
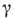- числа. Набор первых интегралов ур-ния
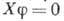таков: 
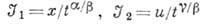, поэтому автомодельное решение ур-ний, допускающих группу растяжений, будет
иметь вид
, 
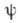-новая
искомая функция.
Рассмотрим, напр., Кортевега - де
Фриса уравнение 
, где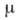 
-пост.
параметр; оно инвариантно относительно преобразования 
, 
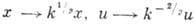. Генератор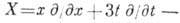
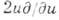-оператор растяжений, и автомодельное решение имеет вид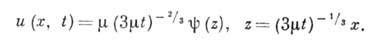 
Подставляя это решение в исходное ур-ние, получаем обыкновенное дифференц. ур-ние для функции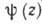
:
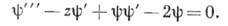
Однопараметрич. группа растяжений абелева. Если система допускает
решения, построенные на др. одно-параметрич. абелевых подгруппах, то
подходящей заменой этим решениям можно придать автомодельный вид, что
является следствием подобия этих групп. В частности, автомодельные
движения тесно связаны с нелинейными бегущими волнами, т. е. решениями вида 
, для к-рых место преобразования подобия занимает преобразование сдвига.
Замена х=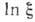
, 
, 
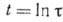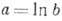переводит волновое решение f в автомодельное:
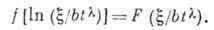
Автомодельность, отражающая внутр. симметрию, присуща
многим явлениям и используется при решении разл. физ. задач, особенно в механике
сплошных сред (см. Автомодельное течение).
Метод ренормализационной группы в квантовой теории поля,
по существу, также основан на использовании автомодельного
преобразования переменных. Интересно, что в автомодельных переменных
ур-ние ренормгруппы оказывается тождественным одномерному ур-нию переноса излучения.
В физике элементарных частиц автомодельность выражается в том, что сечения нек-рых процессов
при высоких энергиях зависят лишь от безразмерных автомодельных
комбинаций импульсов. Общие принципы квантовой теории поля допускают
широкий класс таких автомодельных асимптотик.
В. Е. Рокотян.
Когда тот или иной физик использует понятие "физический вакуум", он либо не понимает абсурдности этого термина, либо лукавит, являясь скрытым или явным приверженцем релятивистской идеологии.
Понять абсурдность этого понятия легче всего обратившись к истокам его возникновения. Рождено оно было Полем Дираком в 1930-х, когда стало ясно, что отрицание эфира в чистом виде, как это делал великий математик, но посредственный физик Анри Пуанкаре, уже нельзя. Слишком много фактов противоречит этому.
Для защиты релятивизма Поль Дирак ввел афизическое и алогичное понятие отрицательной энергии, а затем и существование "моря" двух компенсирующих друг друга энергий в вакууме - положительной и отрицательной, а также "моря" компенсирующих друг друга частиц - виртуальных (то есть кажущихся) электронов и позитронов в вакууме.
Однако такая постановка является внутренне противоречивой (виртуальные частицы ненаблюдаемы и их по произволу можно считать в одном случае отсутствующими, а в другом - присутствующими) и противоречащей релятивизму (то есть отрицанию эфира, так как при наличии таких частиц в вакууме релятивизм уже просто невозможен). Подробнее читайте в FAQ по эфирной физике.
|
|
 |
