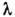 к характерному
размеру течения L - т. н. Кнудсена число
к характерному
размеру течения L - т. н. Кнудсена число 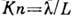 .
.Динамика разреженных газов - раздел механики газов, в к-ром изучаются явления,
требующие учёта молекулярной структуры, привлечения представлений и методов
кинетической теории газов. Толчком к бурному росту исследований в этой
области и образованию на стыке газовой динамики и кинетич. теории газов
самостоятельной дисциплины - Д. р. г.- послужило развитие вакуумной техники
и космонавтики, что и обусловило её название; Д. р. г. наз. также молекулярной
газодинамикой.
В Д. р. г. фундаментальное
значение имеет отношение ср. длины свободного пробега молекул между столкновениями
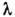 к характерному
размеру течения L - т. н. Кнудсена число
к характерному
размеру течения L - т. н. Кнудсена число 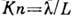 .
.
Классич. газовая динамика
справедлива при 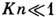 T. к. в этом случае на длине пробега параметры газа изменяются мало, то благодаря
столкновениям молекул в окрестности каждой точки течения устанавливается локальное,
близкое к равновесию состояние, к-рое можно характеризовать неск. макроскопич.
параметрами (плотностью, скоростью, температурой) и производными от них. Это позволяет
прийти к локальному макроскопич. газодинамич. описанию, к представлению о газе
как о сплошной среде (континууме), наделённой нек-рыми
свойствами (вязкостью, теплопроводностью, диффузией и т. д.). Число Kn можно
выразить через параметры континуальной газодинамики - Маха число M и
Рейнольдса число
T. к. в этом случае на длине пробега параметры газа изменяются мало, то благодаря
столкновениям молекул в окрестности каждой точки течения устанавливается локальное,
близкое к равновесию состояние, к-рое можно характеризовать неск. макроскопич.
параметрами (плотностью, скоростью, температурой) и производными от них. Это позволяет
прийти к локальному макроскопич. газодинамич. описанию, к представлению о газе
как о сплошной среде (континууме), наделённой нек-рыми
свойствами (вязкостью, теплопроводностью, диффузией и т. д.). Число Kn можно
выразить через параметры континуальной газодинамики - Маха число M и
Рейнольдса число 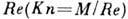 . Отсюда следует, что континуальная газодинамика имеет место при фиксированном
M и
. Отсюда следует, что континуальная газодинамика имеет место при фиксированном
M и  либо при
либо при 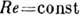 и
и 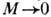 .
.
По мере возрастания числа
Kn состояние газа всё больше отличается от локально равновесного, его
нельзя охарактеризовать конечным числом макропараметров и необходимо перейти
к кинетическому его описанию с помощью функции распределения молекул 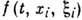 , где t- время, хi - пространств. координаты,
, где t- время, хi - пространств. координаты,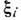 -
компоненты вектора скорости молекул (i=l, 2, 3). Величина
-
компоненты вектора скорости молекул (i=l, 2, 3). Величина 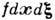 определяет число молекул в момент времени t, имеющих скорости в интервале
определяет число молекул в момент времени t, имеющих скорости в интервале
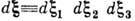 около скорости
около скорости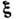 в
элементе пространства
в
элементе пространства 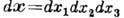 около точки
около точки 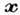 .
Изменение функции f во времени и пространстве описывается кинетическим
уравнением Больцмана:
.
Изменение функции f во времени и пространстве описывается кинетическим
уравнением Больцмана:
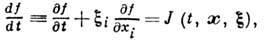
где J - интеграл
столкновений, характеризующий изменение функции распределения f, обусловленное
столкновениями молекул.
Свободномолекулярное
течение. Если 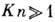 , то столкновениями можно пренебречь. В этом случае
, то столкновениями можно пренебречь. В этом случае 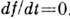 , т. е. функция распределения не изменяется вдоль траектории молекул. Такие течения
наз. свободномолекулярными. Характер явлений при этом определяется столкновением
молекул с ограничивающими течение поверхностями, а следовательно, законами взаимодействия
молекул с жидкими или твёрдыми телами. Явления в свободномолекулярной области
имеют характер, существенно отличный от аналогичных явлений в континуальной
области
, т. е. функция распределения не изменяется вдоль траектории молекул. Такие течения
наз. свободномолекулярными. Характер явлений при этом определяется столкновением
молекул с ограничивающими течение поверхностями, а следовательно, законами взаимодействия
молекул с жидкими или твёрдыми телами. Явления в свободномолекулярной области
имеют характер, существенно отличный от аналогичных явлений в континуальной
области 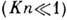 .
Пусть, напр., с двух сторон от нек-рой плоскости газ находится в равновесии
(в покое) при темп-pax T1 и T2 и давлениях
р1 и р2. Если в плоскости имеется отверстие,
диаметр к-рого
.
Пусть, напр., с двух сторон от нек-рой плоскости газ находится в равновесии
(в покое) при темп-pax T1 и T2 и давлениях
р1 и р2. Если в плоскости имеется отверстие,
диаметр к-рого 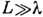 ,
т. е.
,
т. е. 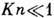 ,
то, согласно законам континуальной газодинамики, газ не будет перетекать через
отверстие, если р1=р2, независимо от температур
T1 и Т2. Если же
,
то, согласно законам континуальной газодинамики, газ не будет перетекать через
отверстие, если р1=р2, независимо от температур
T1 и Т2. Если же 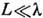 ,
то перетекание отсутствует при условии
,
то перетекание отсутствует при условии 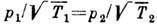 ,
т. к. малое отверстие не нарушает равновесия в каждом из сосудов, а при равновесии
число молекул, проходящих из каждого из сосудов через единицу площади отверстия,
пропорционально произведению плотности
,
т. к. малое отверстие не нарушает равновесия в каждом из сосудов, а при равновесии
число молекул, проходящих из каждого из сосудов через единицу площади отверстия,
пропорционально произведению плотности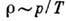 на
ср. скорость теплового движения молекул, пропорциональную
на
ср. скорость теплового движения молекул, пропорциональную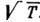 .
.
Характерные особенности
обтекания тел в свободномолекулярном режиме особенно наглядны при гипертермич.
скоростях набегающего потока, т. е. когда скорость потока v много больше
ср. скоростей теплового движения молекул, так что, пренебрегая последними, можно
считать, что все молекулы набегающего потока движутся с одной скоростью v. Если п - число молекул в единице объёма набегающего потока и S - площадь миделевого сечения обтекаемого тела, то число молекул,
падающих на тело, равно 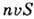 ,
а приносимый ими импульс
,
а приносимый ими импульс 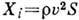 , где
, где 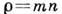 -
плотность, т - масса молекулы. Полная сила сопротивления тела X=Хi+Хr,
где Xr - реактивный импульс отражённых от тела молекул. В
аэродинамике силы, действующие на тело, принято характеризовать безразмерными
аэродинамическими коэффициентами. Если пренебречь импульсом отражённых
молекул, то коэф. сопротивления
-
плотность, т - масса молекулы. Полная сила сопротивления тела X=Хi+Хr,
где Xr - реактивный импульс отражённых от тела молекул. В
аэродинамике силы, действующие на тело, принято характеризовать безразмерными
аэродинамическими коэффициентами. Если пренебречь импульсом отражённых
молекул, то коэф. сопротивления 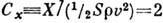 ,
т. о., коэф. сопротивления
,
т. о., коэф. сопротивления 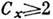 независимо от формы тела. В континуальном же режиме для хорошо обтекаемых тел
Cx порядка сотых или десятых единицы, а для плохо обтекаемых
близок к 1. В свободномолекулярном гипертермич. режиме подъёмная сила обусловлена
лишь реактивным импульсом отражённых молекул. В условиях космич. полёта, напр.,
скорость отражённых молекул
независимо от формы тела. В континуальном же режиме для хорошо обтекаемых тел
Cx порядка сотых или десятых единицы, а для плохо обтекаемых
близок к 1. В свободномолекулярном гипертермич. режиме подъёмная сила обусловлена
лишь реактивным импульсом отражённых молекул. В условиях космич. полёта, напр.,
скорость отражённых молекул 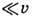 и
и 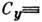
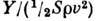 мал, а следовательно, и аэродинамическое
качество
мал, а следовательно, и аэродинамическое
качество 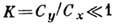 независимо
от формы обтекаемого тела, в то время как в условиях континуума аэродинамич.
качество тел типа крыла может достигать единиц или даже десятков. В условиях
континуума наивысшая темп-pa в потоке, а следовательно, и тел, помещённых в
поток, равна температуре торможения. А в гипертермич. свободномолекулярном потоке
температура теплоизолированного тела (термометра) больше температуры торможения. Если
в условиях континуума в потоке поместить вращающийся цилиндр (рис. 1), то на
него действует подъёмная
сила, направленная вверх,- Магнуса эффект .В свободномолекулярном потоке
отражённые молекулы приобретают составляющую скорости, параллельную поверхности,
так что реактивная сила, действующая на тело, направлена вниз. T. о., характер
явлений в предельных ситуациях
независимо
от формы обтекаемого тела, в то время как в условиях континуума аэродинамич.
качество тел типа крыла может достигать единиц или даже десятков. В условиях
континуума наивысшая темп-pa в потоке, а следовательно, и тел, помещённых в
поток, равна температуре торможения. А в гипертермич. свободномолекулярном потоке
температура теплоизолированного тела (термометра) больше температуры торможения. Если
в условиях континуума в потоке поместить вращающийся цилиндр (рис. 1), то на
него действует подъёмная
сила, направленная вверх,- Магнуса эффект .В свободномолекулярном потоке
отражённые молекулы приобретают составляющую скорости, параллельную поверхности,
так что реактивная сила, действующая на тело, направлена вниз. T. о., характер
явлений в предельных ситуациях 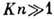 и
и 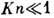 существенно различен. Промежуточная область. Между предельными режимами - континуальным
и свободномолекулярным - лежит переходная область, в к-рой непригодны как континуальное
описание, так и упрощения свободномолекулярного случая. Здесь приходится иметь
дело с решением полного кинетич. ур-ния Больцмана, к-рое много сложнее ур-ний
газовой динамики. Имеется лишь небольшое число точных и аналитич. решений этого
ур-ния для весьма вырожденных ситуаций. Для практически интересных течений решения
получают численными методами. Большое распространение для решения сложных
задач получил метод статистич. моделирования (Монте-Карло метод ),в к-ром
моделируются перелёты и столкновения молекул. Часто для получения приближённых
решений применяют модельные ур-ния с упрощённым интегралом столкновений.
существенно различен. Промежуточная область. Между предельными режимами - континуальным
и свободномолекулярным - лежит переходная область, в к-рой непригодны как континуальное
описание, так и упрощения свободномолекулярного случая. Здесь приходится иметь
дело с решением полного кинетич. ур-ния Больцмана, к-рое много сложнее ур-ний
газовой динамики. Имеется лишь небольшое число точных и аналитич. решений этого
ур-ния для весьма вырожденных ситуаций. Для практически интересных течений решения
получают численными методами. Большое распространение для решения сложных
задач получил метод статистич. моделирования (Монте-Карло метод ),в к-ром
моделируются перелёты и столкновения молекул. Часто для получения приближённых
решений применяют модельные ур-ния с упрощённым интегралом столкновений.
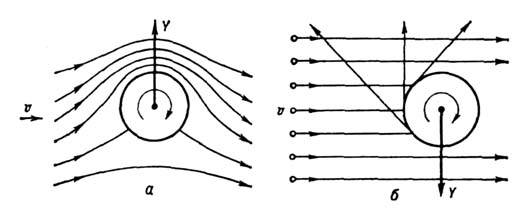
Рис. 1. Схема взаимодействия вращающего цилиндра с потоком: а - континуальным Кn"1 (эффект Магнуса), б - свободномолекулярным Кn"1.
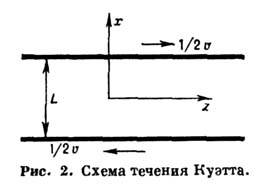
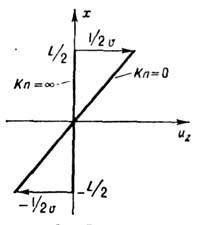
Рис. 3. Распределение скоростей
в течении Kуэтта при различных числах Кнудсена.
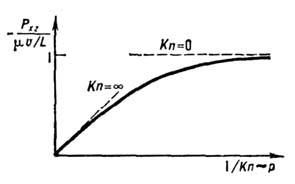
Рис. 4. Напряжение трения между пластинами в течении Куэтта.
Характерные особенности
течений в промежуточной области можно видеть на примере течения Kуэтта: две
бесконечные пластины с равными температура-ми движутся в противоположные стороны
со скоростями 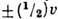 (рис.
2). Если скорость их относит. движения v мала, то на основе приближённого
решения ур-ния Больцмана можно получить выражения для скорости газа uz(x)и постоянного поперёк течения напряжения трения Рхz, к-рые
имеют вид:
(рис.
2). Если скорость их относит. движения v мала, то на основе приближённого
решения ур-ния Больцмана можно получить выражения для скорости газа uz(x)и постоянного поперёк течения напряжения трения Рхz, к-рые
имеют вид:
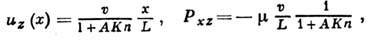
где А - константа,
а 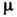 - коэф. вязкости
(рис. 3 и 4). При свободномолекулярном режиме
- коэф. вязкости
(рис. 3 и 4). При свободномолекулярном режиме 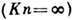 газ между пластинами покоится, несмотря на их движение. На стенках газ "проскальзывает"
на величину
газ между пластинами покоится, несмотря на их движение. На стенках газ "проскальзывает"
на величину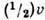 . По мере
уменьшения числа Kn проскальзывание уменьшается, и при
. По мере
уменьшения числа Kn проскальзывание уменьшается, и при 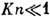 ,
напр. на ниж. поверхности, скорость скольжения
,
напр. на ниж. поверхности, скорость скольжения 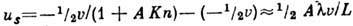 ,
т. е. и в континуальном режиме имеет место проскальзывание, пропорциональное
длине пробега и градиенту
скорости у стенки. T. к. число Kn обратно пропорционально давлению р,
то напряжение трения пропорционально давлению при малых значениях давления
,
т. е. и в континуальном режиме имеет место проскальзывание, пропорциональное
длине пробега и градиенту
скорости у стенки. T. к. число Kn обратно пропорционально давлению р,
то напряжение трения пропорционально давлению при малых значениях давления 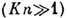 и не зависит от давления в континуальной области, где оно пропорционально коэф.
вязкости ц и градиенту скорости. Если пластины имеют разную температуру, то аналогичная
картина получается для потока тепла, а на стенках имеет место скачок температуры
и не зависит от давления в континуальной области, где оно пропорционально коэф.
вязкости ц и градиенту скорости. Если пластины имеют разную температуру, то аналогичная
картина получается для потока тепла, а на стенках имеет место скачок температуры
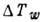 ,
т. е. разрыв между
температурой газа у стенки T и температурой стенки
,
т. е. разрыв между
температурой газа у стенки T и температурой стенки 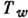 .
Как и для скорости, скачок температуры имеет место и в континуальной области, где
он пропорционален длине пробега и нормальному к стенке градиенту температуры. Принятые
в классич. газодинамике условия прилипания
.
Как и для скорости, скачок температуры имеет место и в континуальной области, где
он пропорционален длине пробега и нормальному к стенке градиенту температуры. Принятые
в классич. газодинамике условия прилипания 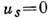 ,
, 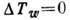 являются приближёнными.
В течении Куэтта напряжение трения или тепловой поток монотонно изменяются с
изменением давления (или Kn)между пластинами. Однако часто в промежуточной
области характеристики меняются немонотонно. Так, в практически важном течении
по плоскому каналу или трубе под действием градиента давления безразмерный объёмный
расход Qp минимален при нек-ром числе Kn (парадокс
Кнудсена; кривая 1 на рис. 5). В континуальной газодинамике с условиями прилипания
на стенке течение в трубе может быть вызвано лишь градиентом давления. В промежуточной
области течение может быть обусловлено также градиентом температуры вдоль трубы.
Если канал или труба соединяет два сосуда с разными температурами, то из-за наличия
градиента температуры вдоль трубы начнётся перетекание из холодного сосуда в горячий.
Для того чтобы ликвидировать перетекание, обусловленное перепадом температуры
являются приближёнными.
В течении Куэтта напряжение трения или тепловой поток монотонно изменяются с
изменением давления (или Kn)между пластинами. Однако часто в промежуточной
области характеристики меняются немонотонно. Так, в практически важном течении
по плоскому каналу или трубе под действием градиента давления безразмерный объёмный
расход Qp минимален при нек-ром числе Kn (парадокс
Кнудсена; кривая 1 на рис. 5). В континуальной газодинамике с условиями прилипания
на стенке течение в трубе может быть вызвано лишь градиентом давления. В промежуточной
области течение может быть обусловлено также градиентом температуры вдоль трубы.
Если канал или труба соединяет два сосуда с разными температурами, то из-за наличия
градиента температуры вдоль трубы начнётся перетекание из холодного сосуда в горячий.
Для того чтобы ликвидировать перетекание, обусловленное перепадом температуры 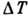 ,
необходимо создать нек-рый перепад давления
,
необходимо создать нек-рый перепад давления 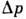 между горячим и холодным сосудами. Величина этого перепада зависит от Kn (рис. 5); его необходимо учитывать, напр., при измерении температуры "горячего"
газа "холодным" манометром. При нулевом расходе газ у стенки течёт
в одну сторону, а в середине канала в другую. Тепловое скольжение, или т. н.
крип, сохраняется и в континуальной области, где оно пропорционально длине пробега
и градиенту температуры вдоль стенки,
между горячим и холодным сосудами. Величина этого перепада зависит от Kn (рис. 5); его необходимо учитывать, напр., при измерении температуры "горячего"
газа "холодным" манометром. При нулевом расходе газ у стенки течёт
в одну сторону, а в середине канала в другую. Тепловое скольжение, или т. н.
крип, сохраняется и в континуальной области, где оно пропорционально длине пробега
и градиенту температуры вдоль стенки,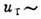
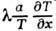 (а - скорость
звука). В отличие от скоростного скольжения
uS и температурного скачка
(а - скорость
звука). В отличие от скоростного скольжения
uS и температурного скачка 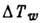 , к-рые приводят лишь к нек-рому отклонению от явлений, имеющих место при условии
прилипания
, к-рые приводят лишь к нек-рому отклонению от явлений, имеющих место при условии
прилипания 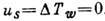 , крипом
обусловлен целый ряд явлений, напр. упомянутое выше движение газа в трубе (термомеханич.
эффект), термофорез
и др. Если тело с коэф. теплопроводности
, крипом
обусловлен целый ряд явлений, напр. упомянутое выше движение газа в трубе (термомеханич.
эффект), термофорез
и др. Если тело с коэф. теплопроводности 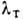 поместить в газ с теплопроводностью
поместить в газ с теплопроводностью 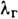 ,
в к-ром имеется градиент температуры, то появится и градиент температуры вдоль поверхности
тела, а следовательно, и скольжение газа от холодной части к горячей. Явления,
вызванные этим движением газа, наз. термофоретическими. T. к. это течение газа
обусловлено телом, то
на тело будет действовать
реактивная термофоретич. сила F в противоположную сторону. Термофорез
имеет место и в промежуточной области (рис. 6). При увеличении теплопроводности
тела его темп-pa выравнивается и термофоретич. сила уменьшается. Если частица
не закреплена, то она будет двигаться со скоростью термофореза, при к-рой её
сопротивление равно термофоретич. силе. В результате термофореза происходит,
напр., осаждение частиц в топках.
,
в к-ром имеется градиент температуры, то появится и градиент температуры вдоль поверхности
тела, а следовательно, и скольжение газа от холодной части к горячей. Явления,
вызванные этим движением газа, наз. термофоретическими. T. к. это течение газа
обусловлено телом, то
на тело будет действовать
реактивная термофоретич. сила F в противоположную сторону. Термофорез
имеет место и в промежуточной области (рис. 6). При увеличении теплопроводности
тела его темп-pa выравнивается и термофоретич. сила уменьшается. Если частица
не закреплена, то она будет двигаться со скоростью термофореза, при к-рой её
сопротивление равно термофоретич. силе. В результате термофореза происходит,
напр., осаждение частиц в топках.
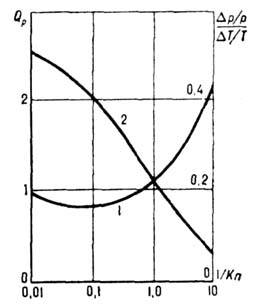
Рис. 5. Парадокс Кнудсена (1); зависимость перепада давления от числа Kn (2).
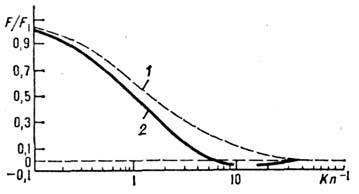
Рис. 6. Изменение термофоретической
силы F в зависимости от числа  :
1 - для
:
1 - для 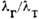 =0,2
и 2 - для
=0,2
и 2 - для 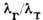 =0,002,
где
=0,002,
где 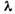 - длина пробега
в окружающем частицу
тазе, d - диаметр частицы, F1 - термофоретическая сила
в свободномолекулярном пределе,
- длина пробега
в окружающем частицу
тазе, d - диаметр частицы, F1 - термофоретическая сила
в свободномолекулярном пределе, 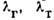 - коэффициенты теплопроводности
газа и тела.
- коэффициенты теплопроводности
газа и тела.
Выше предполагалось, что
в течении имеется лишь одно характерное число Кнудсена, определяющее режим течения.
Однако это не всегда так. При обтекании тел можно выделить несколько характерных
длин пробега (напр., длину пробега набегающих молекул в поле молекул, отражённых
от тела, длину пробега отражённых молекул на набегающих, длину пробега отражённых
молекул на отражённых). При гиперзвуковых скоростях 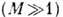 в режиме, близком к свободномолекулярному, эти длины пробега могут существенно
отличаться как друг от друга, так и от длины пробега в набегающем потоке
в режиме, близком к свободномолекулярному, эти длины пробега могут существенно
отличаться как друг от друга, так и от длины пробега в набегающем потоке  .
Величина этих длин пробега зависит от законов взаимодействия молекул между собой
и с телом, от температуры и формы тела. Вместо числа
.
Величина этих длин пробега зависит от законов взаимодействия молекул между собой
и с телом, от температуры и формы тела. Вместо числа  , где L - характерный размер тела, определяющим режим течения может оказаться
число Kn, построенное по одной из указанных характерных длин. Так, напр.,
в условиях натурного космич. полёта характерное число Kn оказывается
в M раз меньше
, где L - характерный размер тела, определяющим режим течения может оказаться
число Kn, построенное по одной из указанных характерных длин. Так, напр.,
в условиях натурного космич. полёта характерное число Kn оказывается
в M раз меньше 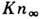 ,
а в условиях аэродинамич. трубы - в M раз больше, т. е. в натурных
условиях при увеличении числа Маха течение удаляется от свободномолекулярного,
а в условиях аэродинамич. трубы стремится к нему. Поэтому при
,
а в условиях аэродинамич. трубы - в M раз больше, т. е. в натурных
условиях при увеличении числа Маха течение удаляется от свободномолекулярного,
а в условиях аэродинамич. трубы стремится к нему. Поэтому при 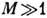 в условиях эксперимента в аэродинамич. трубе свободномолекулярные характеристики
могут достигаться при
в условиях эксперимента в аэродинамич. трубе свободномолекулярные характеристики
могут достигаться при 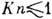 . Это связано с тем, что законы взаимодействия молекул между собой и с телом
существенно зависят от температуры газа и стенки, так что для полного моделирования
недостаточно выдержать натурные значения M и Re, но необходимо
выдержать и натурные значения температуры набегающего потока и тела. В условиях
гиперзвуковой аэродинамич. трубы, как правило, температура набегающего потока ниже,
чем в натурном полёте, а темп-pa тела близка температуре торможения T0, в то время как в полёте большая часть тепла излучается и темп-pa тела оказывается
много меньше T0.
. Это связано с тем, что законы взаимодействия молекул между собой и с телом
существенно зависят от температуры газа и стенки, так что для полного моделирования
недостаточно выдержать натурные значения M и Re, но необходимо
выдержать и натурные значения температуры набегающего потока и тела. В условиях
гиперзвуковой аэродинамич. трубы, как правило, температура набегающего потока ниже,
чем в натурном полёте, а темп-pa тела близка температуре торможения T0, в то время как в полёте большая часть тепла излучается и темп-pa тела оказывается
много меньше T0.
Разл. характер изменения
аэродинамич. характеристик тел разной формы при 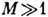 в промежуточной области объясняется также характером столкновения разных групп
молекул. При обтекании тупых тел молекулы набегающего потока рассеиваются на
отражённых молекулах и сопротивление падает по сравнению со свободномолекулярным
течением. При обтекании же тонких тел (пластина, параллельная потоку, тонкий
конус и т. п.) в результате
столкновений на тело попадают молекулы, к-рые без столкновений пролетели бы
мимо тела, и это приводит к возрастанию сопротивления по сравнению со свободномолекулярныи
пределом.
в промежуточной области объясняется также характером столкновения разных групп
молекул. При обтекании тупых тел молекулы набегающего потока рассеиваются на
отражённых молекулах и сопротивление падает по сравнению со свободномолекулярным
течением. При обтекании же тонких тел (пластина, параллельная потоку, тонкий
конус и т. п.) в результате
столкновений на тело попадают молекулы, к-рые без столкновений пролетели бы
мимо тела, и это приводит к возрастанию сопротивления по сравнению со свободномолекулярныи
пределом.
Как уже отмечалось, при
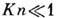 справедливы представления
сплошной среды, т. е. классич. газовой динамики, и применимы Навье - Стокса
уравнения. Однако наряду с основным, "внешним", характерным
размером течения L (напр., размером обтекаемого тела) в течении могут
иметь место "внутренние", или "собственные", характерные
размеры Li, напр. толщина пограничного слоя Прандтля
справедливы представления
сплошной среды, т. е. классич. газовой динамики, и применимы Навье - Стокса
уравнения. Однако наряду с основным, "внешним", характерным
размером течения L (напр., размером обтекаемого тела) в течении могут
иметь место "внутренние", или "собственные", характерные
размеры Li, напр. толщина пограничного слоя Прандтля 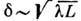 или толщина ударной волны h~
или толщина ударной волны h~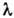 .
Если характерный размер области больше длины пробега молекул, то течение в ней
может быть описано в рамках классич. газодинамики (напр., слой Прандтля). Однако
чем ближе Li к
.
Если характерный размер области больше длины пробега молекул, то течение в ней
может быть описано в рамках классич. газодинамики (напр., слой Прандтля). Однако
чем ближе Li к 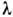 ,
тем менее точным становится такое описание.
,
тем менее точным становится такое описание.
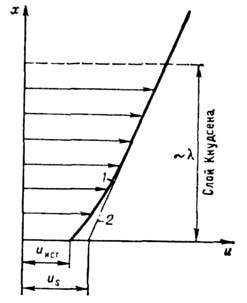
Рис. 7. Течение в слое Кнудсена, х - расстояние по нормали к стенке, и - тангенциальная скорость, uS - скорость скольжения, uист- истинная скорость газа у стенки, 1 - истинный профиль скоростей, 2 - профиль скоростей в решении уравнений Навье - Стокса с условием скольжения на стенке.
Слой Кнудсена. Если
стенка не находится в равновесии с газом, то в общем случае функция распределения
континуального приближения не удовлетворяет микроскопич. граничному условию
на стенке. Поэтому между стенкой и континуальной областью должна существовать
переходная область толщиной порядка длины пробега - слой Кнудсена, в к-рой континуальное
описание неправомерно. Слой Кнудсена, как и ударная
волна, должен
рассматриваться в рамках кинетич. теории с помощью ур-ния Больцмана. В этом
слое распределение газодинамич. параметров, напр. скоростей, имеет вид, показанный
на рис. 7. Скорость скольжения uS не равна истинной скорости
газа у стенки. Решение ур-ния Больцмана в слое Кнудсена связывает справедливое
вне слоя Кнудсена континуальное решение с физ. условиями взаимодействия молекул
с поверхностью тела. При рассмотрении течений во внешней по отношению к кнудсеновскому
слою газодинамич. области истинный ход изменения скоростей или температур внутри
слоя Кнудсена несуществен. Важны лишь скорости скольжения uS,
иТ и скачок температур 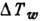 , дающие макроскопич. граничное условие для газодинамич. области на стенке
, дающие макроскопич. граничное условие для газодинамич. области на стенке
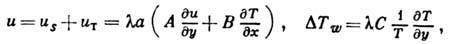
где А, В, С - коэф.,
зависящие от параметров газа у стенки, сорта молекул и закона их взаимодействия
со стенкой. Заметим, что сами представления о газе как о континууме не содержат
к.- л. сведений о граничных условиях на твёрдых или жидких поверхностях (кроме
условия непротекания) и они должны быть получены из дополнит. предположений
или эксперимента. Хотя получаемое с этими граничными условиями решение ур-ний
Навье - Стокса внутри кнудсеновского слоя (прямая 2 на рис. 7) отличается
от истинного решения, потоки тепла и импульса (напряжения трения) к стенке определяются
с точностью, соответствующей точности самих ур-ний газодинамики.
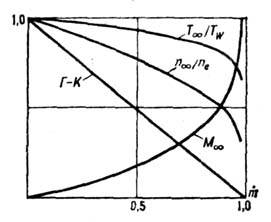
Рис, 8. Зависимость параметров
пара от массы испаряющегося материала; 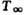 ,
,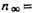
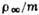 -температура и числовая плотность молекул пара над испаряющей поверхностью (на
границе слоя Кнудсена), nе- числовая плотность насыщенного
пара при температуре поверхности
-температура и числовая плотность молекул пара над испаряющей поверхностью (на
границе слоя Кнудсена), nе- числовая плотность насыщенного
пара при температуре поверхности 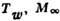 - число Маха нормального к стенке потока на границе
слоя Кнудсена,
- число Маха нормального к стенке потока на границе
слоя Кнудсена, 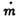 -
масса испарённого материала, отнесённая к массе, которую испарила бы стенка,
если бы молекулы не возвращались на неё в результате столкновений в слое Кнудсена;
Г-К - величина
-
масса испарённого материала, отнесённая к массе, которую испарила бы стенка,
если бы молекулы не возвращались на неё в результате столкновений в слое Кнудсена;
Г-К - величина 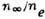 , вычисленная по формуле Герца - Кнудсена.
, вычисленная по формуле Герца - Кнудсена.
Важное значение имеет исследование
слоя Кнудсена При установлении граничных условий для ур-ний газодинамики на
поверхности, на к-рой происходит испарение или гетерогенная реакция. В этом
случае слой Кнудсена связывает континуальные процессы диффузии или течения компонент,
справедливые вне кнудсеновского слоя, с физ. процессами конденсации, испарения
и превращения молекул на поверхности. Анализ течения в кнудсеновском слое показывает,
напр., что даже при предельно сильном испарении, когда на границе кнудсеновского
слоя нормальная к поверхности скорость газа становится равной скорости звука,
часть молекул возвращается на поверхность. Темп-pa испаряющегося газа может
быть существенно меньше температуры испаряющей стенки, а результаты, следующие из
рассмотрения слоя Кнудсена, существенно отличаются от предсказываемых приближённой
ф-лой Герца - Кнудсена (рис. 8). При сильном испарении в свой газ касательная
к поверхности скорость всегда равна нулю, а при конденсации произвольна и определяется
внешним по отношению к кнудсеновскому слою течением. В течении Куэтта с переконденсацией
газа с одной стенки на другую все изменения параметров газа происходят в тонких
слоях Кнудсена, в то время как во всём остальном течении при произвольно большом
расстоянии между пластинами все параметры газа постоянны.
Выше предполагалось, что
при 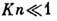 справедливы
ур-ния Навье - Стокса и что отступления от классич. газодинамики вызваны лишь
изменениями граничных условий, обусловленными явлениями в слое Кнудсена. Однако
имеется круг явлений, для к-рых даже при
справедливы
ур-ния Навье - Стокса и что отступления от классич. газодинамики вызваны лишь
изменениями граничных условий, обусловленными явлениями в слое Кнудсена. Однако
имеется круг явлений, для к-рых даже при 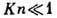 ур-ния Навье - Стокса оказываются несправедливыми.
ур-ния Навье - Стокса оказываются несправедливыми.
Из кинетич. теории газов
следует, что в медленных течениях (т. е. если число 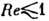 и число
и число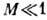 , то
, то 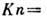
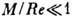 )
при наличии большого перепада температур
)
при наличии большого перепада температур 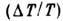 имеют место напряжения в газе, обусловленные градиентами температуры, соизмеримые
с классич. напряжениями, обусловленными градиентами скоростей. Вследствие этих
напряжений даже около равномерно нагретых тел возникает движение газа (термострессовая
конвекция). Это движение газа отличается от гравитационной естественной конвекции
тем, что оно имеет место в отсутствие массовых сил, и от термофореза, к-рый
возникает около тел с неравномерно нагретой поверхностью. Аналогичные явления
обусловлены градиентами концентраций в смесях газов.
имеют место напряжения в газе, обусловленные градиентами температуры, соизмеримые
с классич. напряжениями, обусловленными градиентами скоростей. Вследствие этих
напряжений даже около равномерно нагретых тел возникает движение газа (термострессовая
конвекция). Это движение газа отличается от гравитационной естественной конвекции
тем, что оно имеет место в отсутствие массовых сил, и от термофореза, к-рый
возникает около тел с неравномерно нагретой поверхностью. Аналогичные явления
обусловлены градиентами концентраций в смесях газов.
Истечение струй. Важным
объектом исследований являются струи, истекающие в вакуум или область с низким
давлением. Если истечение струи происходит из форкамеры с достаточно высоким
давлением, то в струе течение может проходить все режимы от сплошной среды до
свободномолекулярного. Вдоль струи темп-pa и плотность падают, а скорость увеличивается.
В струях выражены релаксационные явления: по мере
понижения плотности вдоль струи темп-pa (энергия) внутр. степеней свободы молекул
начинает отставать от температуры (тепловой энергии) поступат. степеней свободы
и затем стабилизируется (замораживается). Далее замораживаются скорость течения
и "продольная" темп-pa (разброс в продольных скоростях молекул).
В струях смесей газов разные газы ведут себя различно, что позволяет использовать
струи разреженного газа для разделения газов и изотопов. При охлаждении газа
в струе может происходить конденсация газа и образование кластеров ,что
широко используется в технологии. T. к. условия образования кластеров для разных
газов различны, то в струях смесей газов можно выделять кластеры разных газов,
получать многослойные кластеры. Путём разгона молекул разл. газов в струе гелия
получают почти "монохроматич." пучки молекул без теплового разброса,
т. е. условия, близкие к абс. нулю температуры. Это позволяет лазерными методами
исследовать свойства молекул, не затушёванные процессами теплового движения
и столкновения молекул.
Экспериментальные исследования.
Для эксперим. исследования течений разреженного газа создаются аэродинамические
трубы низкой плотности (вакуумные трубы), откачка газа в к-рых производится
диффузионными, бустерными или криогенными вакуумными насосами. В соплах таких
труб из-за низкой плотности возникает толстый пограничный слой, поэтому для
получения невозмущённого пограничным слоем ядра потока требуются сопла больших
размеров. Для исследования законов взаимодействия молекул между собой и с поверхностями
используются молекулярные пучки (см. Молекулярное течение ).Специфичны
и методы диагностики потоков разреженного газа. Наряду с высокочувствительными
весами, датчиками давления и потоков тепла (болометры) большое распространение
получила диагностика потока электронными пучками, рентгеновскими лучами, лазерные
методы, использующие флуоресценцию и рассеяние света молекулами.
Вакуумные трубы позволяют
не только изучать явления в разреженных газах, но и исследовать детали мн. явлений
в континуальной области. Разреженность газа, увеличение длины пробега молекул
позволяют "растянуть" течение, как бы посмотреть на него в увеличит.
стекло. Так, ударную волну или кнудсеновский слой, имеющие при нормальных условиях
толщину порядка 10-5 см, можно растянуть до размеров, приемлемых
для исследования их структуры. Струи, истекающие в вакуум, являются удобным
инструментом для изучения релаксационных процессов, определения констант скоростей
хим. реакций, времён релаксации и т. п. Законы движения разреженного газа в
каналах лежат в основе явлений в тонких капиллярах пористых тел. Процессы, имеющие
место при обтекании и испарении тел в разреженном газе, являются элементами
дисперсных двухфазных течений. Явления в кнудсеновском слое определяют характер
гетерогенных, в частности каталитич., реакций, испарения.

M. H. Коган
|
|