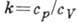и др. Это позволяет определять нагрузки, действующие на натурный объект, по
результатам модельных исследований. А. к. CRA аэродинамич.
силы RA и m аэродинамич. момента M соответственно
равны:Аэродинамические коэффициенты - безразмерные величины, характеризующие аэродинамические силу и момент, действующие на тело, движущееся в жидкой или газообразной среде. В аэродинамике
цель моделирования - определение А. к. при испытании в аэродинамических трубах и др. эксперим. установках моделей, геометрически подобных натурным объектам.
Если в модельных и натурных условиях критерии аэродинамич. подобия (Маха
число M, Рейнольдса число Re, Струхаля число Sh и др.) одинаковы,
а также соблюдается кинематич. подобие, то значения А. к. модели и натуры будут
равны. А. к., как и их проекции на оси координат, не зависят от размерных физ.
свойств среды и размеров тела, а зависят лишь от его формы, ориентации и безразмерных
критериев аэродинамич. подобия, отношения уд. теплоёмкостей среды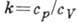
и др. Это позволяет определять нагрузки, действующие на натурный объект, по
результатам модельных исследований. А. к. CRA аэродинамич.
силы RA и m аэродинамич. момента M соответственно
равны:
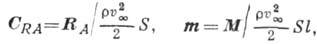
где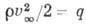
-скоростной напор или динамич. давление,
-
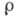плотность среды, в к-рой происходит движение;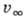 
- скорость движения тела (или скорость невозмущённого набегающего потока в аэродинамич.
трубе); S, l - характерные площадь и линейный размер обтекаемого тела.
Проекции аэродинамич. силы и момента на оси скоростной и связанной систем координат
соответственно (см. рис. 1, 2 к ст. Аэродинамические сила и момент), отнесённые к скоростному напору и геом. параметрам S и l, определяют
значения А. к. лобового сопротивления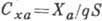 
,
аэродинамич. подъёмной силы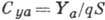 
, аэродинамич. боковой силы 
,
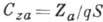коэф. аэродинамич. моментов крена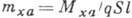 
, рыскания 
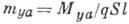и тангажа
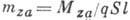(всё в скоростной
системе координат). В связанной системе аналогично определяются А. к. продольной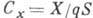
нормальной 
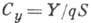, поперечной
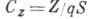сил и соответствующих
моментов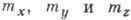 
. Величины
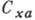и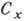 
считаются положительными, когда направлены противоположно оси 
,
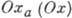остальные составляющие А. к. силы и момента положительны, когда их вектор направлен
по соответствующей оси.
Выбор характерных геом. параметров (S, l), к к-рым принято относить силы и моменты, производится для разных летат. аппаратов разл. способами.
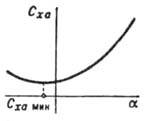
Рис. 1. Зависимость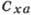 
от угла атаки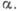
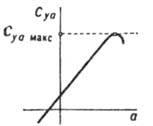
Рис. 2. Зависимость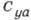 
от угла атаки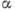
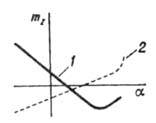
Рис. 3. Зависимость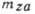 
от угла атаки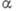
Для самолёта S - площадь
крыла в плане, включая подфюзе-ляжную часть. Для снарядов баллистич. ракет и
слабооперенных летат. аппаратов - это площадь миделевого сечения, т. е. площадь
наибольшего поперечного сечения корпуса (фюзеляжа). При определени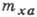и 
и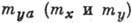 
самолёта в качестве
l принимается размах крыла, а для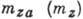 
- его ср. аэродинамич. хорда. В ракетостроении в качестве l используется
длина ракеты. А. к. тела заданной конфигурации при фиксированных
значениях критериев аэродинамич. подобия и установившемся (стационарном) движении
зависят от его ориентации к потоку (от углов атаки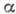
,
скольжения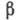
и крена
,
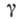рис. 1, 2).
При неустановившемся движении
А. к. зависят также от величин, характеризующих ускорение тела и угловую скорость
его вращения. Поскольку момент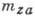 
измеряется относительно принятого центра масс летат. аппарата, по виду зависимости
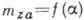(рис. 3), напр.,
можно судить о продольной статич. устойчивости аппарата. Зависимость 1 соответствует
статически устойчивому аппарату, т. к. при отклонении от т. н. балансировочного
угла атаки а, к-рому соответствует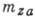 
=0,
возникает момент, возвращающий аппарат в прежнее положение, а кривая 2 - статически
неустойчивому, поскольку действует момент, увеличивающий возникшее отклонение
от балансировочного угла атаки. А. к. зависят также от чисел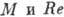 
. Начало возрастания и максимум зависимости 
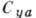(M)(рис. 4) связаны с переходом скорости полёта через скорость звука
(М=1) или с т. н. волновым кризисом. Немонотонность в ср. части зависимости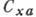
от Re (рис. 5) связана с переходом от ламинарного режима обтекания к
турбулентному.
Значения А. к. необходимы для определения основных лётных характеристик объекта - его сопротивления и подъёмной силы, а также для расчёта его устойчивости и управляемости.
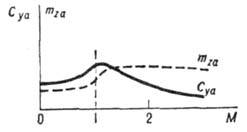
Рис. 4. Зависимость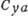 
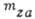от числа M.
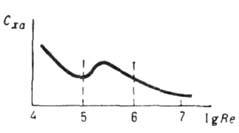
Рис. 5. Зависимость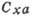 
от числа Re.
Осн. метод определения
А. к. сложных по форме тел-эксперименты на моделях и натурных объектах, хотя
расчётно-теоретич. методы с использованием ЭВМ получают всё большее развитие
и позволяют решать всё более сложные задачи аэродинамики.
Ю. А. Рыжов
1. Электромагнитная волна (в религиозной терминологии релятивизма - "свет") имеет строго постоянную скорость 300 тыс.км/с, абсурдно не отсчитываемую ни от чего. Реально ЭМ-волны имеют разную скорость в веществе (например, ~200 тыс км/с в стекле и ~3 млн. км/с в поверхностных слоях металлов, разную скорость в эфире (см. статью "Температура эфира и красные смещения"), разную скорость для разных частот (см. статью "О скорости ЭМ-волн")
2. В релятивизме "свет" есть мифическое явление само по себе, а не физическая волна, являющаяся волнением определенной физической среды. Релятивистский "свет" - это волнение ничего в ничем. У него нет среды-носителя колебаний.
3. В релятивизме возможны манипуляции со временем (замедление), поэтому там нарушаются основополагающие для любой науки принцип причинности и принцип строгой логичности. В релятивизме при скорости света время останавливается (поэтому в нем абсурдно говорить о частоте фотона). В релятивизме возможны такие насилия над разумом, как утверждение о взаимном превышении возраста близнецов, движущихся с субсветовой скоростью, и прочие издевательства над логикой, присущие любой религии.
4. В гравитационном релятивизме (ОТО) вопреки наблюдаемым фактам утверждается об угловом отклонении ЭМ-волн в пустом пространстве под действием гравитации. Однако астрономам известно, что свет от затменных двойных звезд не подвержен такому отклонению, а те "подтверждающие теорию Эйнштейна факты", которые якобы наблюдались А. Эддингтоном в 1919 году в отношении Солнца, являются фальсификацией. Подробнее читайте в FAQ по эфирной физике.
|
|
 |
