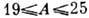 (изотопы
Mg и Al); 2) нейтроноизбыточные ядра с
(изотопы
Mg и Al); 2) нейтроноизбыточные ядра с 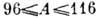 (изотопы Zr, Mo, Ru и Pd); 3) нейтронодефицитные ядра изотопов Xe и Ba с
(изотопы Zr, Mo, Ru и Pd); 3) нейтронодефицитные ядра изотопов Xe и Ba с 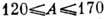 ; 4) ядра редкоземельных
элементов с
; 4) ядра редкоземельных
элементов с 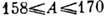 ; 5) ядра актинидов с
; 5) ядра актинидов с 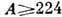 , включая трансурановые элементы.
, включая трансурановые элементы.Деформированные ядра - атомные ядра, форма к-рых в основном состоянии отличается от сферической.
Они имеют аномально большие электрич. квадрупольные моменты Q - в 30
раз больше предсказываемых одночастичной оболочечной моделью ядра. Д.
я. были открыты в 1949 в результате измерения Q. Доказательством их существования
являются спектры возбуждённых состояний Д. я., образующие систему вращат. полос
(см. Вращательное движение ядра).
На каждом состоянии Д.
я. основана вращат. полоса, уровни к-рой имеют определ. чётность и последовательность
угл. моментов I. Для сферич. ядра коллективное вращение (согласно квантовой
механике) невозможно. Коллективное вращение и движение нуклонов в Д. я. в нек-ром
приближении можно считать независимыми (адиабатич. приближение).
В зависимости от числа
нуклонов А (массового числа) существует 5 областей Д. я.: 1) лёгкие ядра
с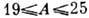 (изотопы
Mg и Al); 2) нейтроноизбыточные ядра с
(изотопы
Mg и Al); 2) нейтроноизбыточные ядра с 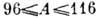 (изотопы Zr, Mo, Ru и Pd); 3) нейтронодефицитные ядра изотопов Xe и Ba с
(изотопы Zr, Mo, Ru и Pd); 3) нейтронодефицитные ядра изотопов Xe и Ba с 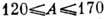 ; 4) ядра редкоземельных
элементов с
; 4) ядра редкоземельных
элементов с 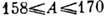 ; 5) ядра актинидов с
; 5) ядра актинидов с 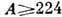 , включая трансурановые элементы.
, включая трансурановые элементы.
Деформация ядер - квантовый
эффект, связанный с оболочечной структурой ядра. Конфигурации заполненных оболочек
сферически симметричны. Напротив, орбиты частиц, не входящих в заполненные оболочки,
анизотропны, что приводит к отклонению формы ядра от сферически симметричной.
Все обнаруженные Д. я. имеют форму вытянутых эллипсоидов вращения. Отклонению
от аксиальной симметрии препятствуют спинорбитальное взаимодействие нуклонов
и парные корреляции нуклонов в ядре (см. ниже). Неаксиальная форма возможна
у самых лёгких Д. я. Неск. нуклонов сверх заполненных оболочек в этих ядрах
составляют значит. часть всех частиц в ядре, что приводит к наибольшим наблюдаемым
деформациям.
Деформация ядер в возбуждённых
состояниях менее изучена. Установлено, что величина Q в состояниях, соответствующих
вращат. полосе, слабо изменяется с ростом полного угл. момента ядра I
до 20. Оболочечные эффекты могут приводить к образованию возбуждённых конфигураций,
форма к-рых существенно отличается от равновесной формы ядра в основном состоянии
(изомеры формы). Наблюдаются высокоспиновые изомерные состояния сферич. ядер,
в к-рых ядро имеет сплюснутую форму (сфероид); пример-деформированные возбуждённые
состояния сферич. ядер 16O и 40Ca с заполненными оболочками.
В Д. я. 5-й области обнаружены спонтанно делящиеся изомеры формы (см. Деление
ядер).
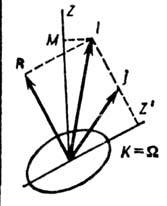
Рис. 1. Схема связи угловых моментов в медленно вращающемся деформированном ядре: R - угловой момент коллективного вращения,j-суммарный угловой момент нуклонов, I - полный угловой момент.
Электрические квадрупольные
моменты и параметры квадрупольной деформации. Большой квадрупольный момент Q у ядер, удалённых от магических ядер, обусловлен
когерентным смешиванием нуклонных оболочечных конфигураций. Аксиальное ядро
характеризуется внутр. электрич. квадрупольным моментом Q0, т.
е. квадрупольным моментом относительно собств. системы координат 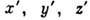 , жёстко связанной с ядром (рис. 1). Вращение ядра приводит к усреднению зарядового
эксцентриситета. Статич. квадрупольный момент Q ядра определяется как
ср. значение этой величины
, жёстко связанной с ядром (рис. 1). Вращение ядра приводит к усреднению зарядового
эксцентриситета. Статич. квадрупольный момент Q ядра определяется как
ср. значение этой величины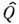 в
состоянии с макс. проекцией (M=I)полного угл. момента I ядра
на выделенное в пространстве направление z (рис. 1):
в
состоянии с макс. проекцией (M=I)полного угл. момента I ядра
на выделенное в пространстве направление z (рис. 1):
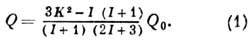
Здесь К - проекция
/ на ось z', совпадающую с осью симметрии Д. я. Для основного состояния ядра
K=I, поэтому:
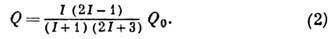
Из (2) видно, что в состояниях
с I=0 и 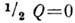 , даже если
, даже если 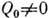 (согласно
квантовой механике, направление оси симметрии ядра в пространстве в этом случае
равновероятно). Величина Q определяется из сверхтонкой структуры атомных спектров, a Q0 - из сечений кулоновского возбуждения
вращат. состояний или их времён жизни (последние измерения дают величину
(согласно
квантовой механике, направление оси симметрии ядра в пространстве в этом случае
равновероятно). Величина Q определяется из сверхтонкой структуры атомных спектров, a Q0 - из сечений кулоновского возбуждения
вращат. состояний или их времён жизни (последние измерения дают величину 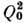 ,
знак Q0 устанавливается по Q; см. Кулоновское возбуждение
ядра).
,
знак Q0 устанавливается по Q; см. Кулоновское возбуждение
ядра).
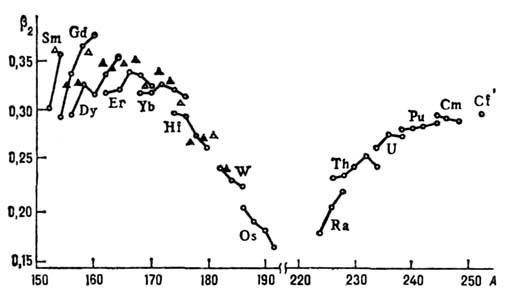
Рис. 2. Параметры b2, квадрупольной деформации основных состояний ядер с А>150;  - четно-чётные ядра,
- четно-чётные ядра,  - нечётно-протонные ядра,
- нечётно-протонные ядра, -
нечетно-нечётные ядра,
-
нечетно-нечётные ядра, -
нечётно-нейтронные ядра.
-
нечётно-нейтронные ядра.
Параметры деформации ядра
определяются по величине Q0 и зависят от распределения плотности
ядерного вещества. В простейшем случае предполагается, что ядро - равномерно
заряженный эллипсоид вращения с полуосями а>b. Плотность распределения
нейтронов и протонов постоянна внутри эллипсоида и равна 0 вне его (модель ядра
с резким краем). Размер ядра определяется среднеквадратичным радиусом 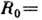
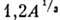 Ферми, а его форма выражением:
Ферми, а его форма выражением:
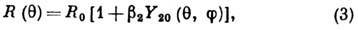
где 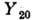 -
сферич. функция, b2 наз. параметром квадрупольной деформации:
-
сферич. функция, b2 наз. параметром квадрупольной деформации:
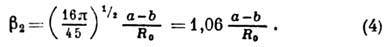
При малых деформациях:
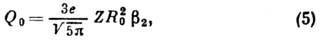
где е - элементарный
заряд. Для больших деформаций 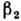 в (5) следует заменить на
в (5) следует заменить на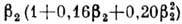
Для Д. я. 4-й и 5-й групп
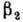 ~0,2- 0,3
(рис. 2), что согласуется с оценкой
~0,2- 0,3
(рис. 2), что согласуется с оценкой 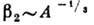 [отношение числа нуклонов вне заполненных оболочек
[отношение числа нуклонов вне заполненных оболочек 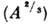 к А]. Ядра с нечётным А и нечётно-нечётные ядра имеют примерно
такую же равновесную деформацию, как и соседние четно-чётные ядра.
к А]. Ядра с нечётным А и нечётно-нечётные ядра имеют примерно
такую же равновесную деформацию, как и соседние четно-чётные ядра.
Др. определение параметра
квадрупольной деформации 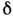 :
:
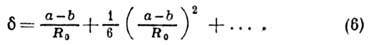
Для него Q0 пропорц. 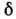 при любой величине деформации. Соотношение между
при любой величине деформации. Соотношение между 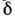 и
и 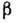 имеет
вид:
имеет
вид:
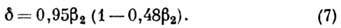
Деформации высших порядков.
Кроме квадрупольной деформации, играющей гл. роль, Д. я. обладают аксиальными
деформациями высш. порядков. Форма ядра, имеющего квадрупольную и гексадекапольную
(4-го порядка) деформации, даётся выражением:
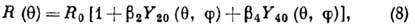
где 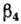 - параметр гексадекапольной деформации (рис. 3). С учётом
- параметр гексадекапольной деформации (рис. 3). С учётом 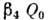 для ядра с резкой границей описывается ф-лой (5), в к-рой
для ядра с резкой границей описывается ф-лой (5), в к-рой 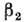 следует заменить на
следует заменить на
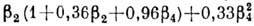
Параметр гексадекапольной
деформации 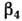 для
редкоземельных ядер меньше 0 и в 20-30 раз меньше
для
редкоземельных ядер меньше 0 и в 20-30 раз меньше 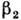 .
.
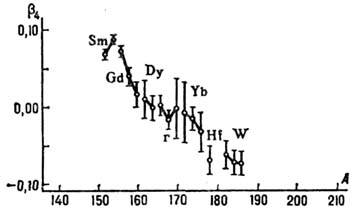
Рис. 3. Гексадекапольные
деформации основных состояний ядер редкоземельных элементов; вертикальные линии
- ошибки измерений.
Структура основных состояний.
Д. я. обладают широким спектром коллективных и одночастичных движений, в к-рых
проявляются как макроскопич. свойства ядра, так и оболочечные (квантовые) эффекты.
Для описания одночастичного движения нуклонов в Д. я. используется несферич.
ср. поле, представляющее собой аксиально-симметричный, квадрупольно-деформированный
потенциал, учитывающий спин-орбитальное взаимодействие нуклонов. Наиб. распространён
т. н. потенциал Нильссона - потенциал анизотропного гармонич. осциллятора. Потенциал
Нильссона имеет бесконечную глубину, поэтому он плохо описывает движение нуклонов
на границе и вне ядра. Ближе к реальному ср. полю ядра потенциал конечной глубины
с размытым краем (потенциал Саксона - Вудса). Для нейтронной и протонной систем
потенциалы поля несколько отличны.
Квантовые числа однонуклонного
движения определяются симметрией ср. поля. Пространств. чётность 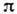 и проекция
и проекция 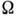 полного угл. момента
полного угл. момента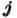 нуклона
на ось симметрии ядра
нуклона
на ось симметрии ядра 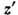 являются интегралами движения. Состояние с данным
являются интегралами движения. Состояние с данным 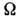 двукратно вырождено, т. к. орбиты, отличающиеся только знаком
двукратно вырождено, т. к. орбиты, отличающиеся только знаком 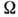 ,
инвариантны относительно отражения времени. Следствием аксиальности деформации
является равенство
,
инвариантны относительно отражения времени. Следствием аксиальности деформации
является равенство 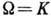 .
.
Для определения др. квантовых
чисел Д. я. важна близость ср. поля ядра к потенциалу гармонич. осциллятора.
В анизотропном осцилляторном потенциале движение разделяется на независимые
колебания вдоль оси z' (квантовое число nz') и в плоскости,
перпендикулярной этой оси 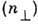 .
Вырожденные состояния с одинаковым
.
Вырожденные состояния с одинаковым 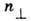 можно характеризовать проекцией
можно характеризовать проекцией 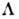 орбитального момента нуклона на ось
орбитального момента нуклона на ось 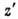 :
:
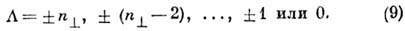
Однако из-за спин-орбитальной
связи ни 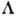 , ни проекция
спина нуклона на ось
, ни проекция
спина нуклона на ось 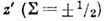 не сохраняются, сохраняется проекция полного угл. момента
не сохраняются, сохраняется проекция полного угл. момента 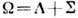 .
.
В реальном ядерном потенциале
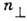 , nz или N, nz (
, nz или N, nz (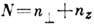 наз. гл. осцилляторным квантовым числом) приближённо сохраняются. Существование
др. пары приближённых квантовых чисел
наз. гл. осцилляторным квантовым числом) приближённо сохраняются. Существование
др. пары приближённых квантовых чисел 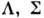 не зависит от конкретного вида потенциала и является следствием аксиальной симметрии
ядра (в несферич. потенциале состояния с различными
не зависит от конкретного вида потенциала и является следствием аксиальной симметрии
ядра (в несферич. потенциале состояния с различными 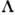 ,
связанные спин-орбитальным взаимодействием, различаются по энергии и поэтому
слабо смешиваются). Четыре приближённых квантовых числа
,
связанные спин-орбитальным взаимодействием, различаются по энергии и поэтому
слабо смешиваются). Четыре приближённых квантовых числа 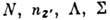 полностью характеризуют состояние нуклона в ср. поле ядра. Для квантовых чисел
однонуклонного движения принята запись:
полностью характеризуют состояние нуклона в ср. поле ядра. Для квантовых чисел
однонуклонного движения принята запись:

причём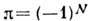 .
.
В основном состоянии четно-чётных
Д. я. уровни ср. поля нейтронов или протонов заполняются нуклонами попарно 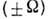 . Такое "выстраивание" орбитального движения нуклонов приводит к
нулевой суммарной проекции угл. момента ядра / на ось симметрии z':
. Такое "выстраивание" орбитального движения нуклонов приводит к
нулевой суммарной проекции угл. момента ядра / на ось симметрии z':
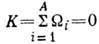 .
.
Последняя заполненная орбита
в нейтронных или протонных конфигурациях наз. энергией 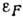 или поверхностью Ферми (энергия Ферми нейтронов
или поверхностью Ферми (энергия Ферми нейтронов 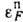 , протонов
, протонов 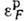 ). У
Д. я. с нечётным числом нуклонов все низшие орбиты попарно заполнены, а нечётный
нуклон занимает низший свободный уровень. Поэтому К и
). У
Д. я. с нечётным числом нуклонов все низшие орбиты попарно заполнены, а нечётный
нуклон занимает низший свободный уровень. Поэтому К и 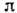 основного состояния нечётного ядра совпадают с
основного состояния нечётного ядра совпадают с 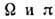 орбиты нечётного нуклона. У нечётно-нечётных Д. я. нечётный нейтрон и протон
находятся на двух разл. орбитах, если число нейтронов и протонов различно. Все
низшие орбиты нейтронов и протонов попарно заполнены. В основном состоянии нейтрон
и протон должны находиться в триплетном спиновом состоянии:
орбиты нечётного нуклона. У нечётно-нечётных Д. я. нечётный нейтрон и протон
находятся на двух разл. орбитах, если число нейтронов и протонов различно. Все
низшие орбиты нейтронов и протонов попарно заполнены. В основном состоянии нейтрон
и протон должны находиться в триплетном спиновом состоянии: 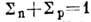 (правило Галлахера - Mошневского), поэтому
(правило Галлахера - Mошневского), поэтому 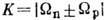 .
.
Возбуждённые состояния
Д. я. Парные корреляции нуклонов. Возбуждённые состояния ядер образуются
при переходе частиц из заполненных уровней на свободные. Незаполненные орбиты
под уровнем Ферми образуют "дырочные" состояния, а заполненные над
уровнем Ферми - "частичные". Возбуждённые состояния определяются
гл. обр. т. н. остаточным взаимодействием между нуклонами, в частности взаимодействием,
переводящим пару нуклонов одного сорта из состояния 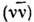 в состояние
в состояние 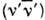 , где
, где
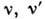 - совокупности
квантовых чисел (10), а
- совокупности
квантовых чисел (10), а 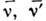 - сопряжённые по времени состояния с проекцией момента -
- сопряжённые по времени состояния с проекцией момента -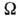 .
Это взаимодействие приводит к парным корреляциям сверхпроводящего типа, к-рые
в Д. я. характеризуются сильным конфигурационным смешиванием уровней
.
Это взаимодействие приводит к парным корреляциям сверхпроводящего типа, к-рые
в Д. я. характеризуются сильным конфигурационным смешиванием уровней 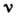 и
и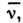 находящихся в
интервале энергий порядка энергии корреляции пары
находящихся в
интервале энергий порядка энергии корреляции пары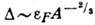 по обе стороны от поверхности Ферми.
по обе стороны от поверхности Ферми.
Парные корреляции в Д.
я. существуют независимо в протонной и нейтронной системах (нейтрон - протонное
спаривание не играет роли). Пара образована нуклонами с противоположным знаком
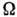 . Число коррелированных
пар
. Число коррелированных
пар 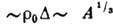 , где
, где 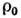 -
плотность одночастичных
уровней у поверхности Ферми. Энергия корреляции
-
плотность одночастичных
уровней у поверхности Ферми. Энергия корреляции 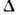 для протонов несколько больше, чем для нейтронов. В среднем для четно-чётных
Д. я. редкоземельных элементов
для протонов несколько больше, чем для нейтронов. В среднем для четно-чётных
Д. я. редкоземельных элементов 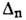 =0,8
МэВ,
=0,8
МэВ, 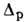 =0,9 МэВ; для
актинидов -
=0,9 МэВ; для
актинидов - 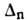 =0,7
МэВ,
=0,7
МэВ, 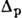 =0,8 МэВ.
=0,8 МэВ.
Несмотря на сильное конфигурационное
смешивание, одночастичное движение нуклонов сохраняет характерные черты, в частности
сохраняются К и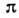 основных состояний ядер. Однако в результате когерентного взаимодействия, в
к-ром участвуют
основных состояний ядер. Однако в результате когерентного взаимодействия, в
к-ром участвуют 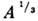 частиц вблизи поверхности Ферми, в ядре возникают элементарные возбуждения,
наз. квазичастицами .Квазичастица представляет собой суперпозицию частицы
и дырки. Основным состоянием четно-чётного ядра является вакуум квазичастиц,
а возбуждённые ядра содержат чётное число квазичастиц. В этих ядрах нет квазичастичных
возбуждений с энергией
частиц вблизи поверхности Ферми, в ядре возникают элементарные возбуждения,
наз. квазичастицами .Квазичастица представляет собой суперпозицию частицы
и дырки. Основным состоянием четно-чётного ядра является вакуум квазичастиц,
а возбуждённые ядра содержат чётное число квазичастиц. В этих ядрах нет квазичастичных
возбуждений с энергией 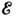 <1,5-2,0
МэВ, т. к. мин. энергия двухквазичастичного возбуждения, связанного с разрывом
пары, равна
<1,5-2,0
МэВ, т. к. мин. энергия двухквазичастичного возбуждения, связанного с разрывом
пары, равна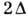 . Энергетич.
щель в спектре возбуждённых состояний четно-чётных Д. я.- характерный признак
парных корреляций сверхпроводящего типа.
. Энергетич.
щель в спектре возбуждённых состояний четно-чётных Д. я.- характерный признак
парных корреляций сверхпроводящего типа.
В основном состоянии нечётных
Д. я. неспаренный нуклон занимает уровни, ближайшие к поверхности Ферми, уменьшая
тем самым объём фазового пространства для взаимодействия остальных нуклонов
того же сорта. Этот т. н. эффект блокировки уменьшает 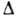 приблизительно на 10-20% по сравнению с чётными Д. я. Возбуждённые уровни нечётных
Д. я. с энергией
приблизительно на 10-20% по сравнению с чётными Д. я. Возбуждённые уровни нечётных
Д. я. с энергией 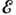 <0,5
МэВ - одноквазичастичные состояния нечётного нуклона. Плотность уровней в этом
интервале энергий примерно вдвое превышает плотность одночастичных состояний
ср. поля ядра, что объясняется характерным спектром одноквазичастичных возбуждений:
<0,5
МэВ - одноквазичастичные состояния нечётного нуклона. Плотность уровней в этом
интервале энергий примерно вдвое превышает плотность одночастичных состояний
ср. поля ядра, что объясняется характерным спектром одноквазичастичных возбуждений:
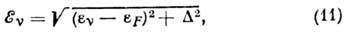
где 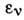 -
энергия нуклона в ср. поле в состоянии с квантовыми числами
-
энергия нуклона в ср. поле в состоянии с квантовыми числами 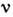 .
При
.
При 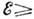 1,5-2,0 МэВ
плотность уровней сильно возрастает из-за появления трёхквазичастичных возбуждений.
В интервале
1,5-2,0 МэВ
плотность уровней сильно возрастает из-за появления трёхквазичастичных возбуждений.
В интервале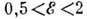 МэВ
плотность возбуждённых уровней также больше одно-квазичастичной из-за состояний,
представляющих собой суперпозицию одноквазичастичных возбуждений с колебательными
(см. Колебательные возбуждения ядер).
МэВ
плотность возбуждённых уровней также больше одно-квазичастичной из-за состояний,
представляющих собой суперпозицию одноквазичастичных возбуждений с колебательными
(см. Колебательные возбуждения ядер).
Магнитный момент Д. я.
обусловлен вращением ядра как целого и внутр. движением нуклонов. Его можно
представить в виде:
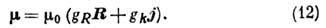
Здесь 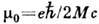 - ядерный магнетон (M - масса нуклона), gR - коллективное
гиромагнитное отношение, gk - внутр. g-фактор,
- ядерный магнетон (M - масса нуклона), gR - коллективное
гиромагнитное отношение, gk - внутр. g-фактор, 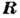 - вращат. момент ядра (рис. 1). В состояниях вращат. полосы с K=0 четно-чётных
Д. я. магн. момент определяется только коллективным вращением:
- вращат. момент ядра (рис. 1). В состояниях вращат. полосы с K=0 четно-чётных
Д. я. магн. момент определяется только коллективным вращением:

В полосах четно-чётных
ядер с 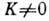 и нечётных
с
и нечётных
с 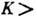
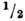 :
:
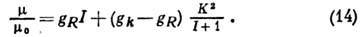
Магн. момент состояний
нечётных ядер с 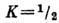 зависит также от т. н. магн. параметра развязывания, к-рый определяется внутр.
структурой ядра.
зависит также от т. н. магн. параметра развязывания, к-рый определяется внутр.
структурой ядра.
Коллективное гиромагн.
отношение gR определяется относит. вкладом протонов во вращат.
движение ядра. Оно равно отношению момента инерции протонов JP к полному моменту инерции ядра 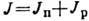 :
:
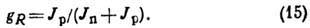
Величина gR
в ср. на 20% меньше значения Z/A, получающегося для равномерно заряженного
вращающегося твёрдого
ядра. В нечётном ядре нечётный нуклон увеличивает либо JP
для нечётно-протонных ядер, либо Jп для нечётно-нейтронных
и коллективный g-фактор первых больше, а вторых меньше, чем gR для соседних четно-чётных ядер. По абс. величине эта четно-нечётная разность
коллективных гиромагнитных отношений 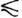 30%.
30%.

И. M. Павличенков.
Когда тот или иной физик использует понятие "физический вакуум", он либо не понимает абсурдности этого термина, либо лукавит, являясь скрытым или явным приверженцем релятивистской идеологии.
Понять абсурдность этого понятия легче всего обратившись к истокам его возникновения. Рождено оно было Полем Дираком в 1930-х, когда стало ясно, что отрицание эфира в чистом виде, как это делал великий математик, но посредственный физик Анри Пуанкаре, уже нельзя. Слишком много фактов противоречит этому.
Для защиты релятивизма Поль Дирак ввел афизическое и алогичное понятие отрицательной энергии, а затем и существование "моря" двух компенсирующих друг друга энергий в вакууме - положительной и отрицательной, а также "моря" компенсирующих друг друга частиц - виртуальных (то есть кажущихся) электронов и позитронов в вакууме.
Однако такая постановка является внутренне противоречивой (виртуальные частицы ненаблюдаемы и их по произволу можно считать в одном случае отсутствующими, а в другом - присутствующими) и противоречащей релятивизму (то есть отрицанию эфира, так как при наличии таких частиц в вакууме релятивизм уже просто невозможен). Подробнее читайте в FAQ по эфирной физике.
|
|