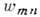 прямого перехода
прямого перехода
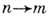 между квантовыми
состояниями п и т равна вероятности обратного перехода
между квантовыми
состояниями п и т равна вероятности обратного перехода  ,
,Детального равновесия принцип (детального баланса принцип) - общий принцип квантовой
механики и статистич. физики, согласно к-рому для изолиров. системы вероятность
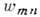 прямого перехода
прямого перехода
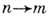 между квантовыми
состояниями п и т равна вероятности обратного перехода
между квантовыми
состояниями п и т равна вероятности обратного перехода  ,
,

Д. р. п. является следствием
осн. принципов квантовой механики, в частности симметрии квантовых ур-ний движения
относительно обращения времени. Если квантовая система взаимодействует
с другой большой системой (термостатом), то, согласно Д. р. п.,
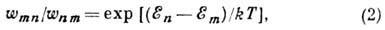
где 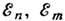 -энергии состояний п и т.
-энергии состояний п и т.
В случае, когда состояния
п и т вырождены или уровни расположены очень плотно, так что вычисляется
вероятность перехода между состояниями в элементах фазового объёма, то, согласно
Д. р. п., равны вероятности перехода, отнесённые к одному конечному состоянию:

где 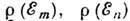 -плотности состояний с энергией em,en.
-плотности состояний с энергией em,en.
Вероятность перехода входит
в кинетическое уравнение основное для вероятности Pn заполнения
квантового уровня п:
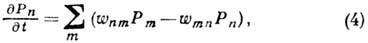
и определяет в случае контакта
с термостатом стремление системы к Гиббса распределению.
Д. р. п. можно формулировать
более детально для парных столкновений частиц (молекул, атомов, элементарных
частиц) с переходом из состояний Г, Г1 в состояния Г', Г1',
где Г - совокупность переменных, определяющих состояние частицы, напр. импульс
р и угл. момент M (функция распределения зависит от Г, координат
центров масс частиц и времени). При обращении знака времени все импульсы и моменты
(а также спины) меняют знак. Поэтому, если Г=(р, M), то после обращения
времени ГТ=(-р,-M). Из симметрии законов движения относительно
обращения времени следует Д.р.п.:
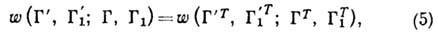
и т. к., согласно Лиувилля
теореме, при обращении времени элемент фазового объёма сохраняется, то число
столкновений с переходом равно числу столкновений с переходом
равно числу столкновений с переходом .
.
Прямой и обращённый во
времени переходы не являются в обычном смысле прямым и обратным, но для одноатомного
газа частиц без спина Д. р. п. справедлив и в буквальном смысле:
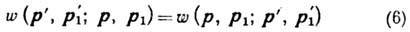
вследствие того, что импульс
не меняется при одновременном обращении времени и инверсии координат. функция
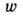 определяет эффективное
сечение в кинетическом уравнении Больцмана.
определяет эффективное
сечение в кинетическом уравнении Больцмана.
Д. р. п. позволяет вычислять
вероятность обратного процесса, если известна вероятность прямого, и наоборот,
что имеет важное значение, т. к. иногда легко измерить эффективное сечение лишь
одного из этих процессов.
Напр., можно вычислить вероятность рекомбинации, зная вероятность ионизации.
Д. р. п. наз. также равенство
ср. числа прямых и обратных столкновений для газов в состоянии статистич. равновесия.
Для газа, подчиняющегося Больцмана статистике, условие детального баланса
есть 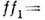
 ,
где
,
где 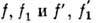 - функции
распределения соответственно до и после столкновения. Из этого условия вытекает
Максвелла распределение .Для квантовых газов условия детального баланса
имеют вид
- функции
распределения соответственно до и после столкновения. Из этого условия вытекает
Максвелла распределение .Для квантовых газов условия детального баланса
имеют вид
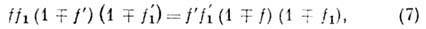
где знаки 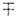 относятся к Ферми - Дирака статистике и Бозе - Эйнштейна статистике. Эти условия определяют распределения Ферми - Дирака и Бозе - Эйнштейна.
относятся к Ферми - Дирака статистике и Бозе - Эйнштейна статистике. Эти условия определяют распределения Ферми - Дирака и Бозе - Эйнштейна.
Лит.: Гайтлер В., Квантовая
теория излучения, пер. с англ., M., 195В, с. 467; Лифшиц E. M., Питаевский Л.
П., Физическая кинетика, M., 1979, с. 17. Д. Н. Зубарев.
Нарушение принципа детального
равновесия. Симметрия относительно обращения времени, на основе к-рой выводится
Д. р. п., является лишь приближённой. Поэтому Д. р. п. также не выполняется
точно. Однако даже малое нарушение Д. р. п. могло бы иметь заметные следствия
в статистич. физике в результате эффекта накапливания нарушения из-за большого
времени существования системы и соответственно большого числа актов столкновения.
Но в равновесном случае этого не происходит, т. к. свойства системы определяются
лишь формой равновесных функций распределения, к-рая, хотя обычно и выводится
из Д. р. п. (как показано выше), фактически не зависит от его справедливости
и может быть получена из более общего принципа унитарности матрицы рассеяния
S.
Амплитуда перехода Аfi из состояния i в состояние f связана с элементом S-матрицы
соотношением
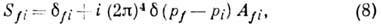
где 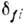 - символ Кронекера,
- символ Кронекера, 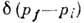 - функция Дирака, pi, pf - 4-импульсы начального
и конечного состояний. Из унитарности условия
- функция Дирака, pi, pf - 4-импульсы начального
и конечного состояний. Из унитарности условия 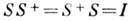 , где I - единичная матрица (S+ - матрица, эрмитово
сопряжённая S), следует:
, где I - единичная матрица (S+ - матрица, эрмитово
сопряжённая S), следует:
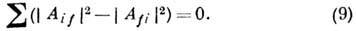
Для вывода равенства (9)
достаточно использовать лишь диагональные элементы матричного равенства  =1, поэтому фактически оно может быть получено из ещё более слабых условий:
СРГ-инвариантности (см. Теорема CPT) и требования, чтобы вероятность
перехода из нач. состояния во все конечные равнялась единице:
=1, поэтому фактически оно может быть получено из ещё более слабых условий:
СРГ-инвариантности (см. Теорема CPT) и требования, чтобы вероятность
перехода из нач. состояния во все конечные равнялась единице:

где 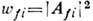 -вероятность перехода из i в f.
-вероятность перехода из i в f.
Соотношение (9) обобщает
условие детального баланса на случай, когда нарушается Т-инвариантность,
и показывает, что в этом случае баланс соблюдается, вообще говоря, не между
каждой отдельной прямой и обратной реакциями, а между суммой переходов из всех
состояний i в состояние f и обратно - из f во все i. Ситуация напоминает кинетич. равновесие электронов в магн. поле, когда отсутствует
детальный баланс в фазовом пространстве, но существует "циклич. баланс":
сколько электронов в среднем утекает влево при их движении по кругу, столько
же притекает справа. Аналогично при нарушении Т-инвариантности баланс
не соблюдается детально между отд. элементами в фазовом пространстве, т. к.
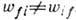 , но выполняется
при учёте всех циклов
, но выполняется
при учёте всех циклов 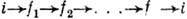 .
В соответствии с этим условие (9) можно назвать условием "циклич. баланса".
.
В соответствии с этим условие (9) можно назвать условием "циклич. баланса".
Используя (9) совместно
с основным кинетич. ур-нием, можно вывести распределение Ферми - Дирака или
Бозе - Эйнштейна в равновесном случае независимо от Д. р. п., поэтому нарушение
симметрии относительно обращения времени в равновесных условиях не проявляется.
Однако в неравновесном случае нарушение Д. р. п. приводит к наблюдаемым эффектам.

А. Д. Долгов
Дело в том, что в его постановке и выводах произведена подмена, аналогичная подмене в школьной шуточной задачке на сообразительность, в которой спрашивается:
- Cколько яблок на березе, если на одной ветке их 5, на другой ветке - 10 и так далее
При этом внимание учеников намеренно отвлекается от того основополагающего факта, что на березе яблоки не растут, в принципе.
В эксперименте Майкельсона ставится вопрос о движении эфира относительно покоящегося в лабораторной системе интерферометра. Однако, если мы ищем эфир, как базовую материю, из которой состоит всё вещество интерферометра, лаборатории, да и Земли в целом, то, естественно, эфир тоже будет неподвижен, так как земное вещество есть всего навсего определенным образом структурированный эфир, и никак не может двигаться относительно самого себя.
Удивительно, что этот цирковой трюк овладел на 120 лет умами физиков на полном серьезе, хотя его прототипы есть в сказках-небылицах всех народов всех времен, включая барона Мюнхаузена, вытащившего себя за волосы из болота, и призванных показать детям возможные жульничества и тем защитить их во взрослой жизни. Подробнее читайте в FAQ по эфирной физике.
|
|