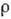Гидродинамика. РЕАЛЬНАЯ ФИЗИКА. Глоссарий по физике

Гидродинамика - раздел гидромеханики, в к-ром изучается движение несжимаемых жидкостей и их взаимодействие с твёрдыми телами или поверхностями раздела с др. жидкостью (газом). Осн. физ. свойствами жидкостей, лежащими в основе построения теоретич. моделей, являются непрерывность, или сплошность, лёгкая подвижность, или текучесть, и вязкость .Большинство капельных жидкостей оказывает значит. сопротивление сжатию и считается практически несжимаемыми.

Методы Г. позволяют рассчитывать скорость, давление и др. параметры жидкости в любой точке занятого жидкостью пространства в любой момент времени. Это даёт возможность определить силы давления и трения, действующие на движущееся в жидкости тело или на стенки канала (русла), являющиеся границами для потока жидкости. Методы Г. пригодны и для газов при скоростях, малых по сравнению со скоростью звука, когда газы ещё можно считать несжимаемыми.

В теоретич. Г. для описания движения несжимаемой (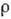

=const) жидкости пользуются неразрывности уравнением

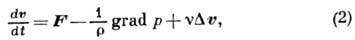
где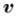

- вектор скорости,

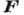- вектор внешних массовых сил, действующих на весь объём жидкости, t - время, 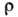- плотность, р - давление, v - коэф. ки-нематич. вязкости. Ур-ние (2) приведено для случая постоянного коэф. вязкости. Искомые параметры v и р являются в общем случае функциями четырёх независимых переменных - координат х, у, z и времени t. Для решения этих ур-ний необходимо задать начальные и граничные условия. Нач. условиями служит задание в нач. момент времени (обычно при t=0) области, занятой жидкостью, и состояния движения. Граничные условия зависят от вида границ. Если граница области - неподвижная твёрдая стенка, то частицы жидкости к ней "прилипают" вследствие вязкости и граничным условием является обращение в нуль всех составляющих скорости на стенке: v=0. B идеальной жидкости, не обладающей вязкостью, это условие заменяется условием "непротекания" (в нуль обращается только нормальная к стенке составляющая скорости: v_n=0). В случае подвижной стенки скорость перемещения любой точки поверхности и скорость частицы жидкости, прилегающей в этой точке, должны быть одинаковы (в идеальной жидкости должны быть одинаковы проекции этих скоростей на нормаль к поверхности). На свободной поверхности жидкости, граничащей с пустотой или с воздухом (газом), должно выполняться граничное условие р(х,у,z,t)=const=p_a, где р_а - давление в окружающем пространстве. Поверхность, удовлетворяющая этому условию, в ряде задач Г. моделирует поверхность раздела жидкости с газом или паром.

Решения систем ур-ний (1) и (2) получены лишь при различных упрощающих предположениях. В отсутствие вязкости (модель идеальной жидкости, в к-рой v=0) они сводятся к Эйлера уравнениям Г. При описании течений жидкости с малой вязкостью (напр., воды) можно упростить ур-ния Г., пользуясь гипотезой о пограничном слое. К упрощению ур-нии Г. приводит также уменьшение числа независимых переменных до трёх - х, у, z или х, у, t, двух - х, у или х, t и одной - х. Если движение жидкости не зависит от времени t, оно наз. установившимся или стационарным. При стационарном движении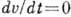

Наиб. развиты методы решения ур-ний идеальной жидкости. Если внешние массовые силы обладают потенциалом:

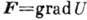, то при стационарном течении ур-ние (2) после интегрирования даёт интеграл Бернулли (см. Бернулли уравнение)в виде

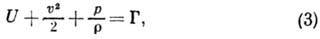
где Г - величина, сохраняющая пост. значение на данной линии тока. Если массовые силы - это силы тяжести, то U=gz (g - ускорение свободного падения) и ур-ние (3) можно свести к виду

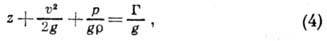
обычно используемому в гидравлике. При безвихревом движении отсутствует вращение частиц в каждой точке жидкости, т. е. имеет место потенциальное течение и скорость , где - потенциал скорости. Для потенциального течения найдены решения многих частных задач: задачи о безотрывном обтекании плоских контуров, о струйных течениях, волновых движениях жидкости, об источниках и стоках, о потенциале простого и двойного слоев и др. (см. также Гармоническая функция).

Успешно решены также мн. задачи о вихревых и волновых движениях идеальной жидкости (о вихревых нитях, слоях, вихревых цепочках, системах вихрей, о волнах на поверхности раздела двух жидкостей, о капиллярных волнах и др.). Развитие вычислит. методов Г. с использованием ЭВМ позволило решить также ряд задач о движении вязкой жидкости, т. е. получить в нек-рых случаях решения полной системы ур-ний (1) и (2) без упрощающих предположений. В случае турбулентного течения, характеризуемого интенсивным перемешиванием отдельных элементарных объёмов жидкости и связанным с этим переносом массы, импульса и теплоты, пользуются моделью "осреднённого" по времени движения, что позволяет правильно описать осн. черты турбулентного течения жидкости и получить важные практич. результаты.

Наряду с теоретич. методами изучения задач Г. применяется лаб. гидродинамич. эксперимент на моделях, основанный на подобия теории. Для этого используют как спец. гидродинамич. моделирующие установки (гидротрубы, гидроканалы, гидролотки), так и аэродинамические трубы малых скоростей, ибо при малых скоростях рабочее тело (воздух) можно считать несжимаемой жидкостью.

Разделами Г. как составной части гидроаэромеханики являются теория движения тел в жидкости, теория фильтрации, теория волновых движений жидкости (в т. ч. теория приливов), теория кавитации, теория глиссирования. Движение неньютоновских жидкостей (не подчиняющихся закону трения Ньютона) рассматривается в реологии. Движение эл--проводных жидкостей в присутствии магн. полей изучает магнитная гидродинамика .Методы Г. позволяют успешно решать задачи гидравлики, гидрологии, русловых потоков, гидротехники, метеорологии, расчёта гидротурбин, насосов, трубопроводов и др.

Литература по гидродинамике

Знаете ли Вы, что такое "усталость света"?
Усталость света, анг. tired light - это явление потери энергии квантом электромагнитного излучения при прохождении космических расстояний, то же самое, что эффект красного смещения спектра далеких галактик, обнаруженный Эдвином Хабблом в 1926 г.
На самом деле кванты света, проходя миллиарды световых лет, отдают свою энергию эфиру, "пустому пространству", так как он является реальной физической средой - носителем электромагнитных колебаний с ненулевой вязкостью или трением, и, следовательно, колебания в этой среде должны затухать с расходом энергии на трение. Трение это чрезвычайно мало, а потому эффект "старения света" или "красное смещение Хаббла" обнаруживается лишь на межгалактических расстояниях.
Таким образом, свет далеких звезд не суммируется со светом ближних. Далекие звезды становятся красными, а совсем далекие уходят в радиодиапазон и перестают быть видимыми вообще. Это реально наблюдаемое явление астрономии глубокого космоса. Подробнее читайте в FAQ по эфирной физике.